Fuzzy_PID控制在空调恒压供水系统中的应用

李建军，刘振兴

(武汉科技大学 信息科学与工程学院，湖北 武汉 430081)

工厂空调控制系统往往具有较大的滞后性和干扰，难以建立精确的数学模型。任何一个环境参数的变化，都可能导致控制系统的不稳定。经典的PID(比例、积分、微分)控制难以得到理想的动态响应特性。针对不同的环境参数及负载大小，需要设定不同的PID控制参数，控制系统自适应能力差。

为了解决上述问题，本文将模糊PID控制策略应用到控制系统中。其最大的优点在于，根据控制系统的输出情况，应用模糊控制规则来最佳调整PID参数，极大地提高控制系统的自适应能力。

1 控制系统的概况[1-2]

控制对象为一工厂的空调恒压供水系统。其基本运行原理为变频器控制水泵运行。要求供水压力为0.5 MPa，在供水管道内有液体压力传感器。压力传感器将检测到的压力值通过变送器转换为标准电流信号后输入PLC的模拟量输入模块。程序根据该输入信号进行PID运算，将得出的值通过模拟量输出模块送给变频器，变频器再输出一定的频率给水泵。整个控制系统大体为：当水压过大时，减小变频器输出频率；反之，当水压变小时，加大变频器输出频率。同时，还有另一台水泵与前一台水泵在电气上并连。当第一台滴水泵故障时，后一台水泵自动投入运转，此即为一用一备。两台水泵的控制策略完全相同。

2 专家-模糊控制器[3]

2.1 模糊控制器原理

模糊控制器以误差e和误差的变化率ec为输入，利用模糊控制规则在线对PID参数进行修改，即得出在相对上一时刻的 3个参数值的变化量ΔKp、ΔKi、ΔKd。 将得出的新的参数值应用到PID控制中，从而使系统输出满足预先的设定值。

图1 模糊PID控制结构图

根据现场情况，计算机能自动调整PID参数。将经典PID与先进的专家系统相结合。首先将长期实践积累的经验知识用控制规则模型化，然后用推理便可对PID参数实现最佳调整。

当e大于设定值时，采用模糊 PID控制；当e小于设定值时，采用一组固定的PID参数进行控制。

2.2 模糊化

在实际应用中，预设的水泵输出压力恒定为0.5MPa。简单起见，这里将E、EC的论域为{-4，-3，-2，-1，0，1，2，3，4}。 E、EC、u 的模糊集均为：{NBB，NB，BM，NS，Z，PS，PM，PB，PBB}，即{负大大，负大，负中，负小，零，正小，正中，正大，正大大}，即以0.1MPa为论域中的一个单位。

模糊控制器的输入为PID控制的3个参数的变化量，即：ΔKp、ΔKi、ΔKd。 将其模糊集为：{NBB，NB，BM，NS，Z，PS，PM，PB，PBB}。

语言变量E、EC各值的隶属函数直接取三角函数[1]。以E为例，其表达式如下：

根据本文中的实际应用，这里实际上NBB=-4，NB=-3，NM=-2，NS=-2，Z=0，PS=1，PM=2，PB=3，PBB=4。

其他2个语言变量EC和u的隶属函数与上面一致。

2.3 建立推理规则

由经典控制理论可知，Kp、Ki、Kd三者作用不同。Kp的作用是提高系统的响应速度，提高系统的调节精度，但是容易产生超调，甚至会使系统不稳定；Ki主要是消除系统静态误差，但如果Ki过大，有可能会在系统响应初期产生积分饱和；Kd的作用是改变系统的动态性能，在响应过程中抵制偏差向任何方向变化，Kd过大，会使响应过程提前制动，延长调节时间，降低系统抗干扰能力[2]。

岩体稀土元素含量∑REE为116.43×10-6，∑Ce/∑Y比值为2.66，δEu为0.61。(La/Sm)N值为3.47，(Gd/Yb)N为0.91；为富轻稀土型。δEu<0.7，表明岩浆为上地壳经不同程度的部分熔融形成的。

当|e|较大时，为了让系统有更好的跟踪性能，应该取较大的|Kp|，这时最容易出现超调，则应控制积分作用，即取较小的|Ki|；当|e|较小时，为了让系统有较好的稳态性能，这里根据经验，取用了一组固定的 Kp、Ki、Kd参数值；当|e|适中时，为了减小超调，应取较小的|Kp|。而为了防止误差变化率过大，|Kd|不应太大。为了避免系统的振荡，当|ec|较小时，|Kd|可以取大些；反之，当|ec|较小时 ，|Kd|可以取小些[3]。

建立控制系统相应的 Kp、Ki、Kd的模糊推理规则如表1所示。表1总共列出了81条推理规则。在程序中表现为 if then语句。例如：if E==NBB a nd EC=NBB，then ΔKp=PBB，ΔKi=NBB，ΔKd=PS。

对于任一时刻的E和EC，经过模糊推理运算，都会得到81条输出结果。实际上，根据E和EC的隶属函数，其模糊集合中的9个等级通常只有1～4个元素有值，其余均为 0，此即为权值。 最终，ΔKp、ΔKi、ΔKd的取值将会根据其模糊集合中各个元素的值与其权值相乘后再相加，最后除以其隶属度和，即可得出最后ΔKp、ΔKi、ΔKd的结果。具体算法可参看参考文献[1]。

表1 模糊推理规则表

最后一步的运算即为：

其中，Kp(k-1)表示在上一个采样时刻 k-1时的 Kp的值，Kp(k)为当前采样时刻k时的Kp的值。

2.4 解模糊

各个参数的解模糊如下所示：

其中 ，Kp′，Ki′，Kd′分别表示由常规方法得到的PID3个参数的值；{e1，ec1}i是采用了模糊控制算法的表述形式，得出ΔKp、ΔKi、ΔKd如下：

μ(E，ΔE)表示隶属度，k 表示权值。

3 仿真结果分析

在Matlab中进行仿真。输入为0.5，即预设定的水泵输出压力[4]。在标准大气压下(即 1.01×105Pa)，对过程前向通道做阶跃响应测试。当检测到输出约为0.5 MPa时，可以得到稳态增益Kc=4.5，时间常数为 Tc=865 s，滞后时间约为34 s。将恒压水泵的预计模型的时间常数取Tc的1/20，时滞取实际的一半[4]。由此，可以估计前向通道的传递函数可表示为：

图2为经典PID控制所得出的系统输出曲线；图3为模糊PID控制所得出的系统输出曲线。二者相比较可以看出，模糊PID算法具有更好的动态响应，响应速度加快，超调变小，稳态误差控制在规定范围内。

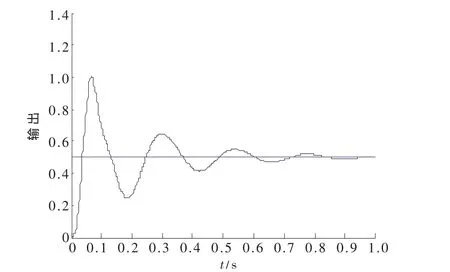
图2 经典PID控制曲线

图3 模糊PID控制曲线

其中，在测试模糊PID控制时，在0.3 s时加入了 1个幅值为0.2的脉冲干扰。可以看到，系统仍旧很快趋于稳定。由此可知，模糊PID控制的鲁棒性较强。

将模糊PID控制应用于恒压水泵控制系统，是在经典PID控制基础上的一次应用创新。它结合了经典PID控制与模糊PID控制的优点，同时也减弱了系统的时滞长的缺点，使系统快速趋于稳定。实践证明，该方法取得了理想的控制效果，完全实现了控制系统的自动化，节省了人力，提高了工作效率，为工厂的正常作业与生产提供了有力的保障。

[1]刘金琨.先进 PID控制 MATLAB仿真[M].北京：电子工业出版社，2004.

[2]胡寿松.自动控制原理[M].北京：科学出版社，2006.

[3]李可.专家-模糊PID在低速风洞风速控制系统中的应用[J].北京航空航天大学学报，2007，33(12)：1387-1390.

[4]张静.MATLAB在控制系统中的应用[M].北京：电子工业出版社，2007.