自适应小波去噪算法及其在偏心补偿中的应用

李道平,姚小兰,伍清河,曲亦直

(北京理工大学 自动化学院, 北京 100081)

小波变换由于在时域和频域同时具有良好的局部化性质[1],对指定频带和时间段内的信号成分进行分析,因此成为工程应用中有力的工具. 在液压自动厚度控制(AGC)系统中,利用小波变换对包含噪声的轧辊偏心信号进行阈值去噪,并利用重构信号反向叠加以补偿原偏心信号是近年来出现的新方法[2],但是常规的小波去噪方法不容易找到最优的阈值设定,会滤掉有用信号或者不能达到良好的去噪效果. 作者根据噪声在小波变换下的特性自适应地确定小波分解的阈值,并将去噪信号的信噪比(SNR)作为滤波器参数的函数,采用一种缩小区间的搜索算法——黄金分割法[3]进行寻优,得到最优的阈值参数.

1 自适应小波阈值去噪算法

1.1 小波变换及其Mallat算法

文献[4]中给出了多分辨分析的概念,并利用双尺度方程和小波方程得到了递推的塔式算法,即Mallat算法.

设φ(x)为尺度函数,φ(x)为小波基函数,hn和gn为φ(x)所对应的小波变换的共轭镜像滤波器,则信号f(x)可分解为如下形式：

(1)

式中：cJ,k为尺度函数的展开系数；dj,k为小波展开系数.f(x)的正交小波变换分解公式为

(2)

式(2)由cj+1,k计算cj,k和dj,k的算法称为Mallat分解算法. 利用该算法可以很容易地计算出各个不同分辨层上的小波展开系数dj,k(j=J-1,J-2,…,J-M)和在较“粗”尺度子空间中的尺度函数展开系数cJ-M,k.

1.2 黄金分割法

黄金分割法[3]是一种常用的缩小区间的搜索算法,该方法每次选取整个不确定区间的两个黄金分割点,通过比较该两点值的大小,缩小搜索的区间.

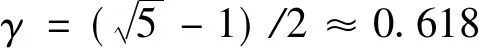
1.3 自适应小波阈值去噪算法

将轧辊偏心信号利用小波变换的Mallat算法对其进行分解,对不同尺度上小波变换的系数进行阈值处理,然后再重构得到新信号. 目前最常用的阈值去噪方法主要有硬阈值法和软阈值法[5].

设采样信号具有如下形式：

f(k)=s(k)+σB(k),(k=0,1,2,…,N-1).

(3)

式中：s(k)为有用信号；B(k)为噪声；σ为噪声的标准差；N为采样次数. 设wj,k为f(k)的离散小波变换的系数,则wj,k由两部分组成：一部分是有用信号s(k)对应的小波系数,记为uj,k；一部分是噪声序列对应的小波系数,记为vj,k.

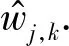
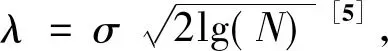
(4)

而软阈值法定义为

(5)

新阈值函数[6]如下：

(6)

图1 自适应小波滤波器结构

2 基于自适应小波阈值去噪算法的轧辊偏心补偿系统

由于液压AGC系统中轧辊偏心的存在,实际的板厚会减少. 但是,由于轧制压力的增大,会使系统认为是板厚增大,因而在控制器的作用下系统朝着使板厚减少的方向动作,结果使控制效果恶化. 因此,在液压AGC系统中,抑制轧辊偏心和消除来料厚度波动有冲突,必须将轧辊的偏心信号从厚度控制系统中分离出来,对其单独进行补偿,从而消除轧辊偏心的影响.

根据上述的思想,作者设计了一个轧辊偏心补偿系统,其对应的液压AGC系统如图2所示.

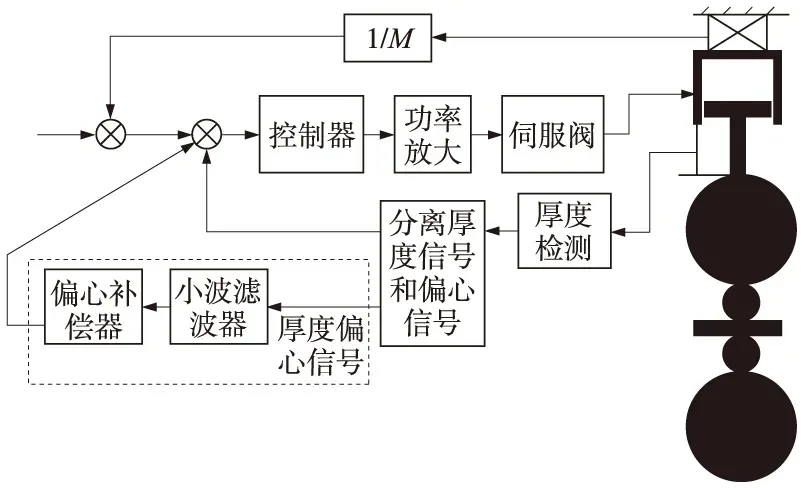
图2 带有轧辊偏心补偿系统的液压AGC系统

首先在厚度反馈信号中提取出带有噪声的轧辊偏心信号,在小波滤波器中利用上述算法去除信号中的噪声. 由于重构的信号与原有偏心信号的差别主要在于幅值的变化和相位的变化,需要偏心补偿器对其进行幅值和相位的补偿,在下一偏心信号周期时反向叠加到原有的液压AGC系统中. 系统的幅值由原有信号的标准差和去噪信号的标准差比值决定. 由于偏心信号是一个周期信号,设T为偏心信号的周期,τ为算法计算和设备延时等的时间,因此只需要人为做一个延时t=T-τ,在下一周期将其加载到系统中,因此系统的信号每周期实时得到更新,补偿信号也得到更新并在下一周期加载到系统中,从而实时自适应地去除噪声并对系统进行补偿.

3 系统仿真

设采样信号如式(3)所示,式中B(k)取服从N(0,1)分布的标准白噪声.

设连续信号s(t)的表达式为

s(t)=0.1sin (2πt+0.2)+0.06sin (2π×

1.02t+1.1)+0.05sin (2π×2t+0.8)+

0.03sin (2π×2.06t+1.6).

(7)

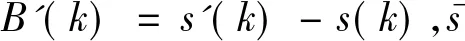
σs为信号的标准差,噪声的幅度取为信号幅度的0.4倍,即σ=0.4σs.

信噪比定义为

由于dbN小波具有计算量小等特点,实验中选取dbN小波. 对于分解尺度的选取,过高的分解尺度会带来较大的计算量,并且在实验中发现并非分解尺度越高去噪性能越好,经过权衡后选取尺度为4.

以阈值函数的参数α为自变量,信噪比RSN作为函数值绘制的曲线如图3所示.

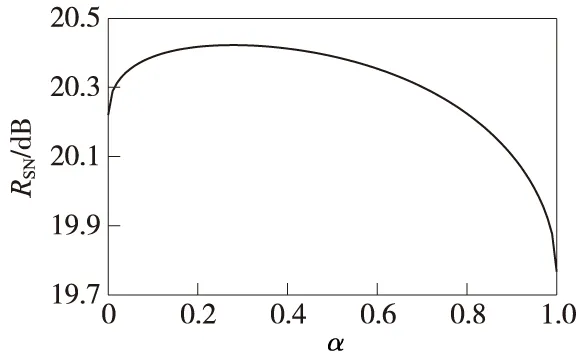
图3 RSN随参数α变化曲线

从图3中可以看出,对于轧辊的偏心信号,信噪比RSN是α的强单峰函数,存在最大值点,比α=0时采用的硬阈值法和α=1时的软阈值法的去噪效果都要好. 因此利用缩小区间的搜索算法可以寻找到最大值点. 表1为采用黄金分割法迭代20步的寻优结果.

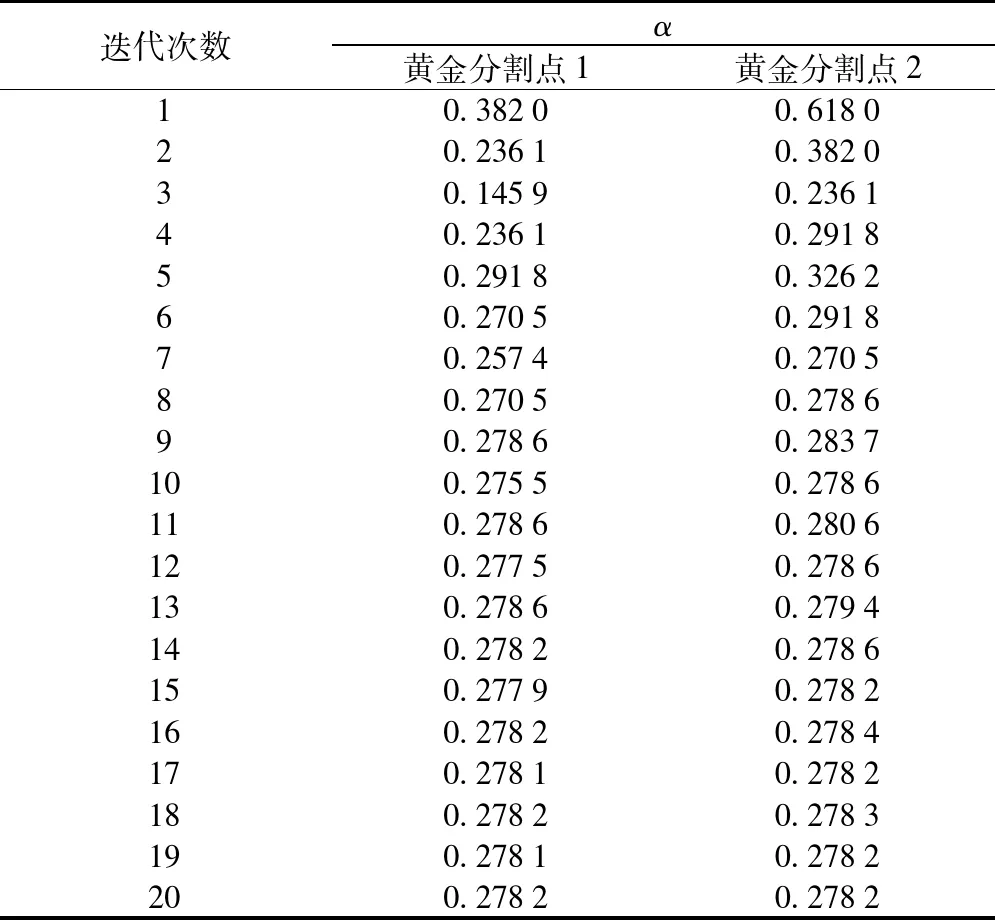
表1 黄金分割法迭代20步的寻优结果

最终迭代的结果为两个黄金分割点的中点α=0.278 2,RSN=20.422 0,比采用软阈值法α=1的信噪比结果RSN=20.398 3和硬阈值法α=0的信噪比结果RSN=19.767 5都要大,而且可以看出文献[6]中取α=0.5,RSN=20.389 6的折中方法并不是最好的结果.

图4是原信号、染噪信号和采用新阈值去噪算法重构信号的结果并与软阈值法和硬阈值法结果的比较. 图5是采用新算法对系统补偿后的残差与采用软阈值法和硬阈值法结果的比较. 从图4和图5中可以看出,采用新算法重构的小波信号既削弱了采用硬阈值法带来的振荡,也减小了采用软阈值法带来的恒定偏差. 系统的残差比软阈值法和硬阈值法都小,有效地重构了偏心信号,并且由于新算法的信噪比最高,因此补偿后的效果也是最好的,有效地实现了偏心信号的补偿.

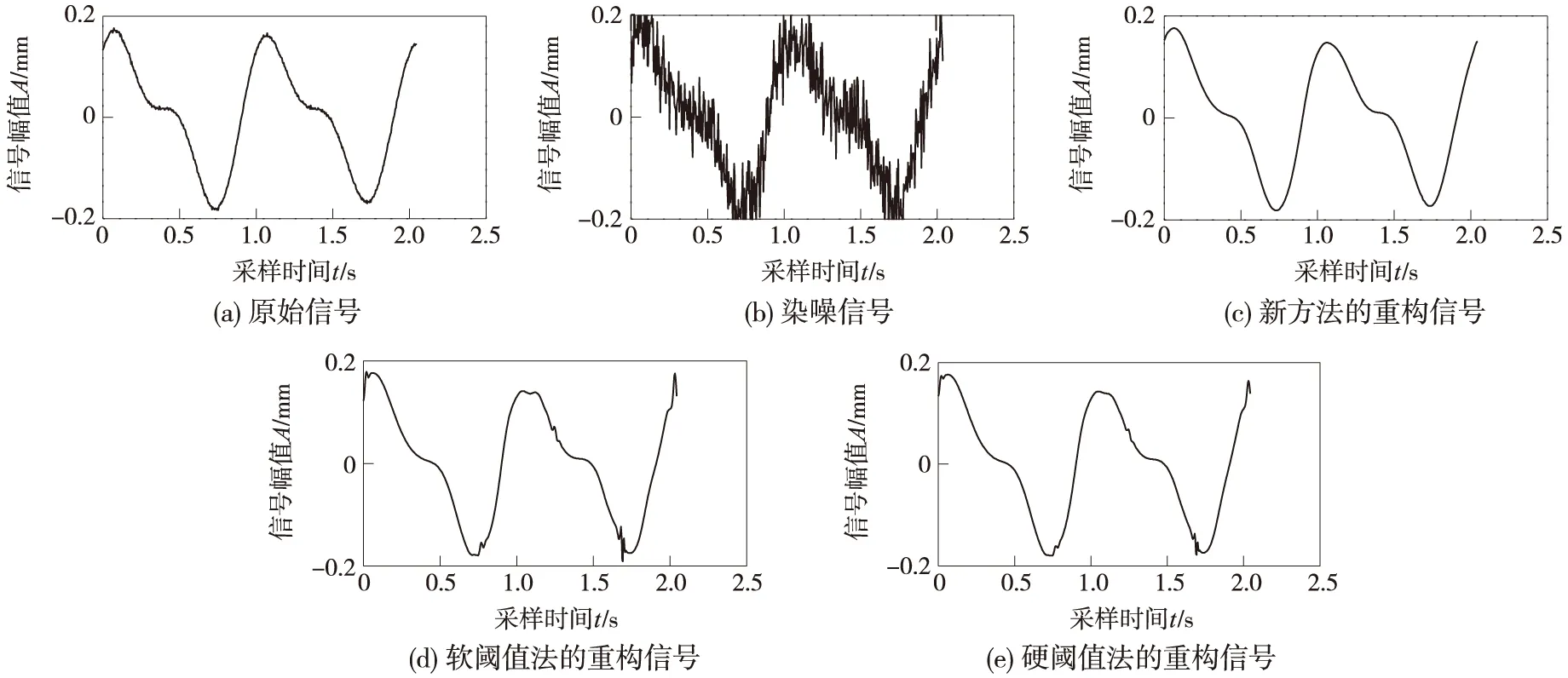
图4 新阈值去噪算法的结果及与软阈值法和硬阈值法的比较

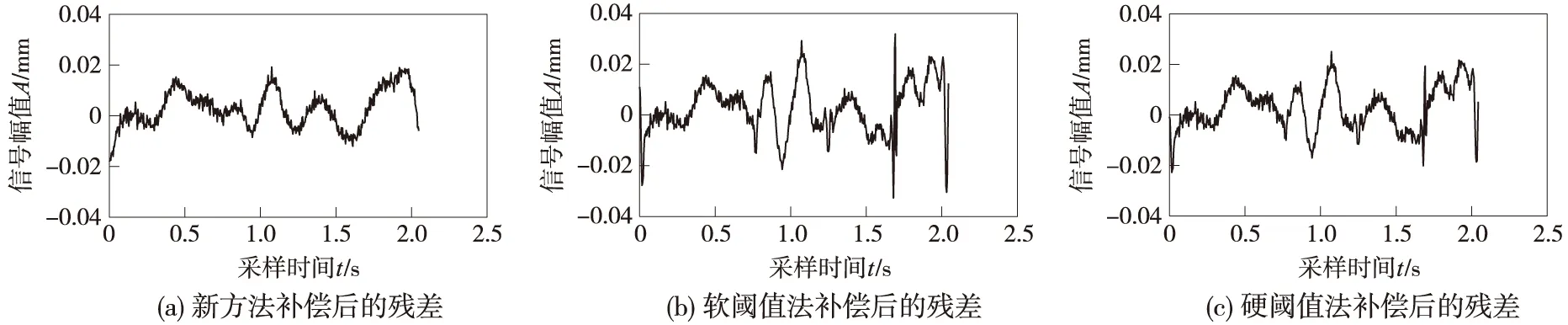
图5 新阈值去噪算法补偿后的残差及与软阈值法和硬阈值法的比较

4 结 论

根据噪声小波系数的特征,通过分析得出新的自适应小波阈值去噪算法,对小波系数阈值量化方法进行了改进,利用黄金分割法找到了最优的阈值

参数,实现了信号的高质量去噪,并将其应用到液压AGC系统中,有效地实现了对轧辊偏心信号的补偿.

参考文献：

[1]Driesen J. Analyzing time-varying system harmonics using wavelet transform[C]∥Proceedings of IEEE Instrumentation and Measurement Technology Conference. Brussels：TEEE Press, 1996：474-479.

[2]李勇.基于自适应小波阈值法的AGC系统[J].钢铁,2007,42(1)：39-44．

Li Yong. AGC system with adaptive threshold method of wavelet transform[J]. Iron & Steel,2007,42(1)：39-44. (in Chinese)

[3]吴祈宗.运筹学与最优化方法[M].北京：机械工业出版社,2003．

Wu Qizong. Operations research and optimization[M]. Beijing：China Machine Press, 2003.(in Chinese)

[4]Mallat S. Theory for multi-resolution signal decomposition: the wavelet representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1989,11(7)：674-693．

[5]Donoho D L. De-noising by soft-thresholding[J]. IEEE Trans Inform Theory,1995,41(3)：613-627．

[6]张文娟.小波阈值去噪的一种改进方案[J].电脑开发与应用,2007,20(1)：28-29．

Zhang Wenjuan. A modified method of wavelet thresholding denoising[J]. The Development and Application of Computer, 2007,20(1)：28-29.(in Chinese)