内平动全摆线齿轮压力角的分析

刘令涛,焦永和,张春林， 赵自强

(北京理工大学 机械与车辆学院, 北京 100081)

内平动齿轮传动是少齿数齿轮传动的一种,具有传动比大、体积小、重量轻、性能可靠、传动效率高、承载能力大、运转平稳等优点. 目前内平动齿轮多采用渐开线齿形,它存在自身的缺点：传动时,齿面之间的滑动摩擦较大,而且又是两个凸面相接触,接触的单位压力大,齿面较易磨损；因为受到根切的限制,渐开线齿轮的设计齿数不能太少,因此在传动比要求大时,机构尺寸相对较大[1-2].

摆线齿轮以其无根切、体积小、传动平稳、重合度大等优点更多地被应用到一些精度要求很高的场合,在军械、钟表等行业应用很广泛. 将全摆线齿形用于内平动齿轮代替原有的渐开线齿形应用于内平动齿轮传动装置中,这种全摆线齿轮的齿廓完全由内外摆线构成,没有通常的齿顶和齿根,基圆和分度圆重合[3].

国内对平动齿轮传动的研究很多,但仅限于渐开线齿形,对摆线齿形的研究几乎处于空白. 为了将这种全摆线齿轮应用于平动齿轮机构中,有必要对其进行深入研究[3]. 压力角是度量一个机构传动力性能好坏的重要指标,在机构受力分析、效率计算和优化设计中都是一个非常重要的参数. 作者推导了全摆线齿轮齿廓上任一点的压力角计算公式,并得出了变化规律及与其它参数的关系.

1 全摆线齿轮压力角的推导

(1)

式中θ为直线MO与轴x的夹角.

图1 全摆线齿轮的压力角

在坐标系x1Oy1中,其内摆线AB的参数方程为

(2)

式中θ′为直线NO与轴x1的夹角.

在PA段,设其上任一点M的法线为Fn1,斜率为k1,则

(3)

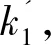
(4)

设该点的压力角为α1,则

(5)

将式(3)(4)带入式(5)，可以得到外摆线压力角α1的计算公式为

α1=arctan|tan[R1/(2r1)]θ|，

θ∈[0,2πr1/R1].

(6)

同理在AB段,可以得到内摆线上任一点N的压力角α2的计算公式为

α2=arctan |tan [R1/(2r2)]θ′|，

θ′∈[0,2πr2/R1].

(7)

2 全摆线齿轮压力角的影响参数

2.1 全摆线齿轮的重合度

ε=(πr1+πr2)/p=0.5.

(8)

图2 全摆线齿轮的啮合线

为了确保全摆线齿轮传动的连续性,必须使用斜齿摆线齿轮来代替直齿.

2.2 滚圆半径不同时的压力角

应用全摆线齿轮的压力角计算公式(6)和式(7),通过选取模数m、齿数z和滚圆半径r,在Matlab软件中编制程序来绘制全摆线齿轮一个轮齿的压力角变化曲线,找出影响压力角大小的参数.

图3所示为全摆线齿轮的模数m=10mm,z=20,r1,r2分别取不同值时,其一个轮齿传动中压力角的变化曲线图.

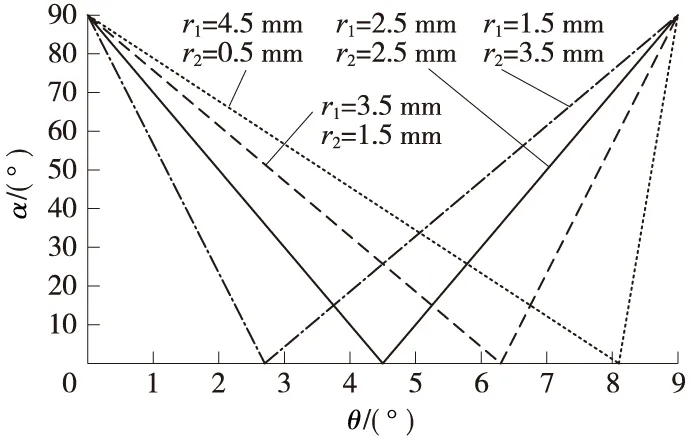
图3 滚圆半径不同时轮齿的压力角变化曲线

由图3可知全摆线齿轮的压力角随着转角的变化呈线性变化；根据受力分析可知,齿轮的压力角越小,主动轮推动从动轮转动的有效分力越大,对传动越有利,即传动效率高,但是机械强度差；齿轮压力角越大,主动轮推动从动轮转动的有效分力越小,对传动越不利,即传动效率低,但机械强度高；而当压力角接近90°时,则基本认为主动轮对从动轮的转动不起作用. 由于全摆线齿轮的压力角在[0,90°]范围内连续变化,在内摆线和外摆线的交点处,压力角α=0,主动轮推动从动轮的力全部有效；在全摆线齿轮的齿顶和齿根处,其压力角α=90°,此时主动轮齿轮传递失效,为齿轮传动的最不利点. 因此,在实际应用中,必须修正齿廓的齿顶和齿根处曲线,使压力角小于90°,而且其压力角的变化范围越小越好,以保证传动的稳定性.

在齿顶齿廓和齿根齿廓上,全摆线齿轮压力角的变化速率并不相同,反映在图中即为直线的斜率不同；当且仅当r1=r2时,压力角在整个齿廓的变化速率才始终保持一致.

2.3 滚圆半径相同时的压力角

由摆线齿轮的性质可知,当齿轮的模数选定后,其滚圆半径也就相应确定,其关系为r=m/4.

图4为模数m=10mm,滚圆半径r1=r2=2.5mm,齿数z=20,30,40时,其一个轮齿传动过程中压力角α的变化曲线图.

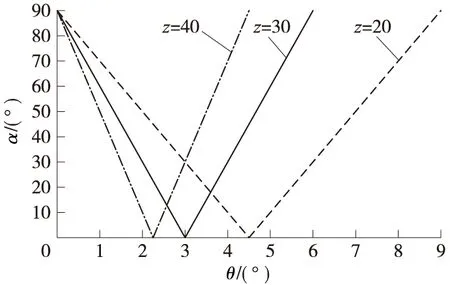
图4 滚圆半径相同、齿数不同时齿轮的压力角变化曲线

由摆线的性质可知,当两个滚圆的半径相等时,其半径的大小随模数的变化而变化,但必须保证r=m/4这一潜在的等式关系. 此时压力角的计算公式简化为

α=arctan |tan (zθ)|，θ∈[0,π/z].

(9)

由式(9)可以看出,这种全摆线齿轮的压力角与模数无关,只与摆线齿轮的齿数有关. 其变化曲线如图5所示. 由图5可见，这种摆线齿轮的压力角变化速率相同,而且在整个轮齿的啮合过程中与模数没有任何关系,为其应用的通用性奠定了基础.

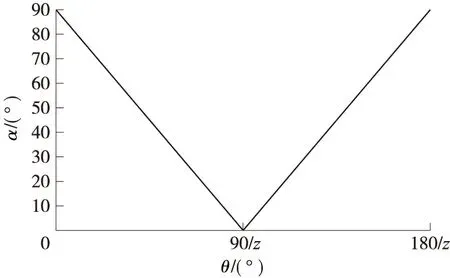
图5 r1=r2时的摆线齿轮压力角变化曲线

3 结 论

根据齿轮啮合基本定律和摆线的性质,推导出全摆线齿轮齿廓上压力角的通用计算公式,并结合实例得出了全摆线齿轮压力角和其它齿轮参数即模数m、齿数z和滚圆半径r的关系,得到如下结论.

① 全摆线齿轮应该用斜齿轮代替直齿轮来保证齿轮传动的连续性.

② 在齿轮的齿顶和齿根处应进行修正,以保证齿轮传动的有效性.

③ 应保证全摆线齿轮的两个滚圆半径相等,以保证齿轮传动的平稳性.

④ 在滚圆半径相等的情况下,压力角由齿轮的齿数决定,与模数无关.

内平动全摆线齿轮压力角分析,证明了全摆线齿轮应用在内平动齿轮机构中的可能性,为后续的内平动全摆线齿轮的优化设计提供了理论依据. 进一步工作是对轮廓曲线进行修正,使其能应用于实际工作中.

参考文献：

[1]张春林,荣辉,黄祖德.圆平动齿轮传动机构的研究[J].北京理工大学学报,1996,16(3):267-272．

Zhang Chunlin, Rong Hui, Huang Zude. A study on circular parallel translation gears[J]. Jounral of Beijing Institute of Technology,1996,16(3):267-272. (in Chinese)

[2]张春林,姚九成.平动齿轮机构的基本型与其演化的研究[J].机械设计与研究,1998(3):29-30．

Zhang Chunlin, Yao Jiucheng. A study of the basic pattern and its evolution of the parallel move gear mechanism[J]. Machine Design and Research,1998(3):29-30. (in Chinese)

[3]汤海燕.内平动摆线齿轮传动运动机理的研究[D].北京:北京理工大学机械与车辆工程学院,2006．

Tang Haiyan. A study on the mechanism of cycloid internal parallel move gears[D]. Beijing: School of Mechanical and Vehicular Engineering, Beijing Institute of Technology,2006. (in Chinese)

[4]吴序堂.齿轮啮合原理[M].北京:机械工业出版社,1982：1-55．

Wu Xutang. Gear meshing principle[M]. Beijing: China Machine Press,1982：1-55. (in Chinese)

[5]李特文Φ Л.齿轮啮合原理[M].佚名,译.2版.上海:上海科学技术出版社,1984：210-232．

Лигвин Φ Л. Gear meshing principle[M]. Anon, transl.2nd ed. Shanghai: Shanghai Science & Technology Press,1984：210-232. (in Chinese)

[6]Litvin F L, Feng Pinhao. Computerized design and generation of cycloidal gearings[J]. Mach Theory,1996(7):891-911.

[7]Shin Joongho, Chang Sewon, Kwon Soonman, et al. New shape design method of an epicycloidal gear for an epicycloid drive[C]∥Proc of SPIE. [S.l.]: SPIE,2005,6040:60401G1～60401G6．