含高斯函数项方程解的探索*
2010-05-16韩祥临范光欢
韩祥临 ,范光欢
(湖州师范学院 理学院, 浙江 湖州 313000)
1 预备知识
高斯函数是现代数论函数中的一个重要函数,它在近现代数论和其它数学学科都有相当广泛的应用,并频频地出现于各个级别的数学竞赛中,这足以显示出它的重要地位。这类问题的解决需要对它的定义、性质作深刻的理解,并且解题要求有很强的技巧。这里,我们先简述高斯函数的定义和基本性质[1-2],为探讨含高斯函数项方程的求解方法做准备。
定义:高斯函数[x]又称取整函数,即对任意实数x,x是不超过 的最大整数,称[x]为x的整数部分,与它相伴随的{x}是小数部分。
性质:(1)y=[x]的定义域为R,值域为Z;(2)y={x}的定义域为R,值域为[0,1);(3)对任意实数x,都有x=[x]+{x},且0≤{x}<1;(4)对任意实数x,都有[x]≤x<[x]+1,x-1<[x]≤x⟺x-1<[x]≤x<[x]+1;(5)若[x]=n,则n≤x 含高斯函数的方程已经由许多学者从不同角度进行了探讨[3-7],这里结合具体实例对相关方法进行归类总结,并进一步进行分析。 含高斯函数项方程中主要类型为[f(x)]=g(x)型,其中f(x),g(x)均为有理系数多项式,解决此类方程主要应用换元法。此方法主要应用了[x]为整数,令g(x)=t,并结合性质(3)、(4)、(5)确定t的取值,最后根据t的取值情况求出x的值。 说明:(1)当方程形如{f(x)}=g(x)时,应用定义x=[x]+{x}将{f(x)}转化为f(x)-[f(x)],这样便把问题转化成了[f(x)]=g(x)型;(2)当方程形如{f(x)}=g(x)时,利用性质(3)有0≤g(x)<1,进而可求出 的范围,从而确定f(x)的取值范围,最后就可求解x的值;(3)之前所用的换元法都是将[f(x)]=g(x)中的g(x)换为整数t,事实上,若令[g(x)]=n,再由性质5对原方程进行变换,求出n,从而确定x,也可以很容易地解决含高斯函数的方程。此类换元适合f(x),g(x)都为1次或2次整系数多项式的情形。 图像法作为解决问题的一个常用方法,在含高斯函数项方程中,由于y=[x]的图像为阶梯形。充分利用这一特点,采用图像法可使问题变得简单。 例2:解方程x3-[x]=3 该方法充分利用了性质(4),用x-1和x分别作为替代[x]的上下界,得到一个关于x的不等式组,解此不等式组确定x的可能取值,经验证得到x的取值。该方法适用于方程中只含一个高斯函数项的情形。特别是当方程形似于普通一元二次方程的情形。 例3:求方程3x2-20[x]+12=0的实数解 解:由x-1<[x]≤x可将原方程化为不等式组 (1) 构造法有两种情形:(1)由定义构造,即利用x=[x]+{x}或x=n+r,(n∈Z,0≤r<1)变形原方程;(2)配方法。在使用构造法时所要求的技巧很强,必需对题目进行充分地分析。 例4:求x3-[x]=3的解 大家熟知的配方法(事实上也是变形法的一种)在解高斯函数方程中也有出现。 此方法实质上为分类讨论法。当方程中含有高次多项式,特别是当该高次多项式所对应的函数图像是不熟悉的无法准确作图,甚至无法作图时,该方法就充分体现了其优越性(其思想类似于含绝对值方程中的去绝对值过程)。 例6:解方程3x3-[x]=3 这里重点讨论形如[f(x)]=[g(x)]的方程的求解,可用性质8若[x]=[y],则|x-y|<1求解。 (3) 于是,由性质6 当1-2x∈Z时, 因为含高斯函数项方程求解的方法具有多样性和灵活性的特点,所以对这类问题的求解比较困难。本文从六个方面分类予以探讨,并举例进行了分析与说明。这无论对大学数学的教学与研究,还是对中学生的思维都有一定的帮助,并且此类题使得学生有机会接触到经典的数学知识,对提高中小学生的学习兴趣也有相当的益处。当然,含高斯函数项方程求解是一个非常困难的大课题,今后我们还有待继续予以深入地研究。 参考文献: [1] 闵嗣鹤,严士健.初等数论[M]. 北京:高等教育出版社,2003:19-23. [2] 王进明.初等数论[M].北京:人民教育出版社,2002:77-102. [3] 王朝霞.含有 及 的方程的解法[J].唐山师范学院学报,2004,(5):56-58. [4] 宋庆龙.高斯函数的应用[J].唐山师范学院学报,2005,(2): 60. [5] 陈少娜.高斯函数问题求解方法简析[J].海南大学学报(自然科学版),2008,(4): 379. [6] 徐彦明.关于高斯函数的竞赛题[J].中学数学月刊,2002,(4):40. [7] 王一松,苏顺英.高斯函数及其应用[J].德阳教育学报,2000,(2):19.2 含高斯函数方程解的探求
2.1 换元法



2.2 图像法

2.3 放缩法
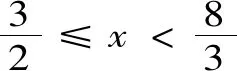

2.4 构造法


2.5 分区间讨论法

2.6 一类特殊方程的解法
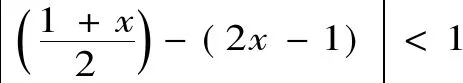


3 结语
