模糊神经网络控制在风力发电系统中的应用*

郝晓弘 ，史宁波 ，高 超

(1.兰州理工大学 电气工程与信息工程学院，甘肃 兰州 730050；2.哈电发电设备国家工程研究中心有限公司 自动化控制部，黑龙江 哈尔滨 150036)

风力发电过程中，需要在额定风速以上保持功率在额定值以满足风电系统自身的机械电气强度要求，实现系统的优化运行。参考文献[1]应用模糊控制算法设计出模糊控制器。参考文献[2]基于模糊逻辑推理系统采用变论域自适应模糊控制器实现了较高的控制精度。但是简单模糊控制器的缺点是模糊规则的获取及隶属度函数的确定主要依靠专家经验而没有统一的方法，缺乏自适应能力。因此研究先进的模糊控制算法及其在大型风力发电机组中的应用，改善机组的控制性能，是风力发电机组控制领域的主要研究热点之一。

基于以上分析，本文将神经网络应用于模糊系统，将两者结合设计出的控制器可用网络实现模糊映射过程，学习的目标是根据输入-输出训练数据自动地提取控制规则，确定前件和后件参数。

1 风力发电机组的控制原理及控制方式

根据贝兹理论，风力机从风中捕捉到的机械功率如下：

式中：Pm为风轮吸收的功率(W)；ρ为空气密度(kg/m3)；ν为风速(m/s)；A为风力机的扫琼面积(m2)；Cp为风能利用系数，反映了风轮机利用风能的效率，λ为叶尖速比，β为桨叶节距角。

为了在有效获取风能的同时保证安全运行，风力机应该工作在下面3个与风速、最大允许转子速度和额定功率有关的基本模式下，如图1所示。图1中：vw0为风力机切入风速；vw1为达到最大允许转速时的风速；vw2为额定风速；vw3为切出风速。

模式I：变速、最大风能利用系数 Cp，max

给定风速vw在额定值以下时，风力机叶片桨距角β被固定在最优值βopt。风力机通过不断调整转速以工作在最佳叶尖速比λopt时刻，从而获得最大风能利用系数Cp，max实现风力机的效率最大化。 发电机转速参考值 ωt，opt可以表示为：

式中：R为风力机风轮半径。

模式II：定速、变叶尖速比

当风速上升使风力机转速达到限制值后，风能利用系数Cp将减小但由于转矩的增大使风力机捕获的风能将继续增加。

模式III：变速、定功率输出

当风速超出额定值，因发电机和功率变换器的容量限制，必须要限制从风中捕获的能量。这时应将发电机转速和输出功率稳定在额定值。风速达到切出风速后，系统将出于保护风力机的目的而停机。

2 桨距角模糊神经网络控制

2.1 模糊神经网络的结构

变桨距功率控制是机组起动后变桨距系统最主要的任务，其控制效果是评价变桨距系统的重要依据。本文采用FMLP模糊神经网络结构，该网络主要是根据模糊系统的结构来决定等价结构的神经网络，使神经网络的每个层、每个节点对应模糊系统的一部分。该网络模型共分5层，如图2所示，它是具有1个输入层、3个隐含层和1个输出层的5层神经网络[3]。

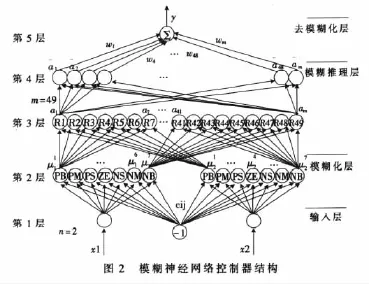
模糊神经网络(FNN)融合了模糊逻辑系统和神经网络的优点，具有很强的自学习能力，可以自动地产生模糊规则和调整隶属度函数。

第1层为输入层，该层为输入变量层，每个节点代表经过预处理过的输入变量x=[x1x2…xn]T，本设计的该层节点数 n=2，即 x=[E EC]T，采用功率误差 E=Pref-P，及功率误差变化率EC为输入变量。

第2层为隶属函数层，实现输入变量的模糊化(即隶属度划分)，隶属度函数(激活函数)采用高斯函数：

式中：i=1，2，…n，j=1，2，…mi，n 是输入变量维数，mi是xi的模糊分割数。每个节点代表一个语言变量值，如PB、NS等，节点的个数为各个输入变量的模糊集合数之和，本文取 mi=7。

第3层为模糊规则强度匹配层，每个节点代表一条模糊规则，计算出每条规则的适用度：

式中：i1∈{1，2，…m1}，i2∈{1，2，…m2}，…in∈{1，2，…mn}，j=1，2， …m，mmi，总的节点个数 m=7×7=49。

第4层为归一化层，节点数与第3层相同，每个节点代表一个可能的模糊规则的then部分：

式中：j=1，2，…m

第5层为反模糊化层，用于实现清晰化计算，将模糊规则推理得到的输出变量的各个模糊集合的隶属度值(第4层各个节点的输出)，转换为输出变量桨距角变化的精确数值：

式中：i=1，2，…r，本文取 r=1，wij写为 wj相当于 yj的第j个语言隶属函数的中心值，在模糊神经网络控制系统中，任意的k时刻，49条规则中只有1条推理得到的规则有输出，其他48条规则输出均为0。

2.2 模糊神经网络的学习算法

根据以上定义的FNN各层节点的操作，各输入变量的模糊分割数个数已预先确定，现在需要学习的参数主要是最后一层的连接权值wj，以及第2层的隶属度函数的中心值cij和宽度σij。下面推导出针对这种FNN的误差反向传播学习算法(FBP算法)来修正网络的可调参数。定义FBP算法的目标函数为[4]：

式中：yd和y分别为教师信号和实际输出，根据FBP算法误差信号将由第5层向第2层依次反向传递。利用一阶梯度寻优算法调节参数 wj、cij、σij。

第5层反传误差信号公式：

权值修正：

第4层反传误差信号公式：

第3层反传误差信号公式：

第2层反传误差信号公式：

中心值和宽度调整公式：

其中，i＝1，2；j=1，2，…7。 η 为按梯度搜索的步长，0<η<1。k为离散时间变量。

该模糊神经网络和BP网络及CMAC等一样，本质上也是实现从输入到输出的非线性映射。结构上是多层前馈网，学习算法是通过误差反传的方法，和CMAC一样属于局部逼近网络。

3 仿真结果

通过图3的变桨距控制原理建立机组各部分模型的连接。风速在额定值以下时通过调节发电机转速进行速度控制追踪最大功率输出，额定值以上通过桨距角的调节保证风力机在额定功率发电。

在进行学习前，必须提供输入输出训练数据对、隶属函数形状、输入数据的模糊论域个数。再利用神经网络的有效学习算法，从这些数据中学习控制规则和隶属函数。本文预先给定了输入的隶属度函数，如图4所示。需调整的参数只有输出层的连接权值wj(j=1，2，…m)。根据变桨距控制问题本身定义输入层为功率误差E及功率误差变化率EC，并在训练前将网络训练数据规范到论域(-6，6)之间，输出层为桨距角变化量。

运用Matlab语言实现网络并进行训练，选择120组隶属度值作为训练样本，当网络达到误差精度要求时，结束训练过程。每次训练的迭代次数取1 000次，训练结束MSE为 1.34785×10-7，训练过程误差曲线如图5所示，训练误差在允许误差范围内。再通过13组数据作为测试样本，误差均小于0.5。这说明基于Fussy-Neuro网络模型可以比较准确地充分描述输入与输出之间的映射关系，具有较好的容错能力和学习能力，能补偿风力机的固有的非线性和整个系统的不可预测性，如参数随时间时刻变化。

由于风轮机械响应比电磁响应慢得多，发电机和电力电子器件的动态特性没有包含在仿真模型中，桨距角幅值限制在 0～20°之间，变桨距速率为 5°/s。仿真模型的数据采用国产兆瓦级变速恒频直驱风电机组的主要相关技术参数，如表1所示。

表1 仿真风电机组的主要参数

在相同风速条件下，采用PI控制器与本文提出的模糊神经网络控制器作为对比仿真，结果如图6所示。

由仿真结果可知，该模糊神经网络控制器在高风速时能控制桨叶节距角的变化使功率保持在额定值附近且具有较小的波动，比同种状态下采用PI控制器的控制效果优越，非常适用于时变的风力发电系统微处理器控制。

针对额定风速以上情况，本文设计并验证了一种适用于风电系统的模糊神经网络控制器。该控制器基于实时数据进行计算，因此能够不断优化其内部参数使系统可以克服非线性及时变性，满足了系统的动态特性和稳态性能。FNN控制策略不但具有一般模糊控制的优点，而且具有神经网络的自学习能力。仿真结果表明了提出方法的有效性，高风速时，模糊神经网络控制器的控制效果比采用功率的PI控制方法更适用于当今的风力发电系统。

[1]刘新海，于书芳.模糊控制在大型风力发电机控制中的应用[J].自动化仪表，2004，25(5)∶13-17.

[2]张新房，徐大平，吕跃刚，等.大型变速风力发电机组的自适应模糊控制[J].系统仿真学报，2004，16(3)∶573-577.

[3]侯媛彬，杜京义，汪梅.神经网络[M].西安：西安电子科技大学出版社，2007.

[4]杨宇姝，冯江，曹然.模糊神经网络在施肥决策系统的应 用[J].农 机 化 研 究，2004(3)∶175-179.