基于Simulink的取样锁相环非线性分析

李 欣

(华南理工大学 广州汽车学院电子信息工程系，广东 广州 510800)

取样锁相环SPLL(Sampling Phase-Locked Loop)是一种数模混合的锁相环路，具有数字环与模拟环的特点。通过取样鉴相，环路可将输出信号频率锁定在输入信号的某次谐波或分频波上，其特点是寄生输出小，可实现高次倍频和分频，在现代频率合成与微波固态源中有广泛的应用[1]。所以取样锁相环的好坏直接影响整个系统的性能。要想改善取样锁相环的非线性性能，优化系统设计，必须要研究取样锁相环的非线性性质。目前，关于取样锁相环的非线性性质分析的文献较少，本文借助Matlab仿真工具箱中的Simulink建立了二阶取样锁相环在Simulink环境下的仿真模型并进行仿真，分析了时间常数、环路增益与采样周期对捕获时间的影响，提出了改善二阶SPLL的非线性性能的途径，优化设计系统。

1 二阶SPLL在Simulink环境下的仿真模型

取样锁相环有倍频环和分频环两种，本文以倍频环为例，建立Simulink环境下的仿真模型。倍频取样锁相环的电路模型[2]如图1所示。

令图中m=1，即将输出信号频率锁定在输入信号频率的基波频率上。取样锁相环的近似相位模型如图2所示。

图1 取样锁相环

图2 取样锁相环的相位模型

其中 θ1为输入的相位信号，θ2为输出相位信号，θe为相位误差信号 G0(s)为保持器，F(s)为低通滤波器的传递函数，kω/s为压控振荡器的拉氏变换 kd为鉴相器增益，kω为压控器增益。设输入的突变信号θ1(t)为单位斜升信号，且令 kd=1，则 K(环路增益)=kdkω=kω(这种假设不影响取样锁相环的非线性特性)，则二阶取样锁相环在Simulink环境下的仿真模型如图3所示(采用零阶保持器)[3]。

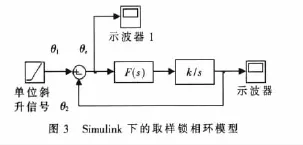
图3中示波器测得取样锁相环的输出信号 θ1，示波器1测得相位误差信号θe。图中得到的模型是连续模型，必须将其转化为离散模型进行仿真。在Simulink环境Tools下，Model descretizer的下拉选项中选定模型 Z变换的方法(零阶保持)；在Sample time中输入采样周期T；在Replace selection with的下拉选项中选定变换后的模型参数显示(Discrete blocks(Enter parameters in z-do main))，最后进行模型转换，即可得到变换后的离散模型，从而可以方便地仿真出不同参数条件下系统的输出信号及相位误差信号。

2 二阶取样锁相环的非线性特性

本文以二阶无源比例积分取样锁相环(即取样锁相环的低通滤波器采用无源比例积分滤波器)为例，进行取样锁相环在不同条件下的Simulink仿真。

无源比例积分滤波器传递函数的拉氏变换[4]为：

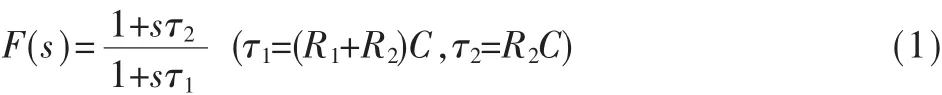
将式(1)带入到图3的Simulink模型中，并进行模型转换与仿真，从而得到在不同条件下的系统输出和相位误差信号波形。

输入相位信号θ1为单位斜升信号的波形，如图4所示。

2.1 非线性性能与时间常数的关系[5]

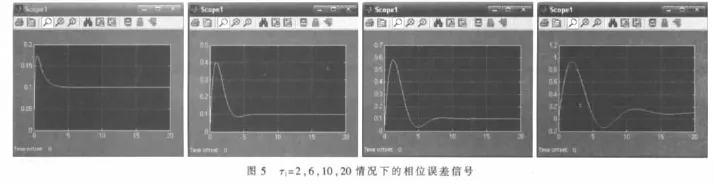
(1)当环路增益、采样周期和时间常数 τ2固定(K=10，T=0.05 s，τ2=1)时，改变时间常数 τ1，τ1分别为 2、6、10、20，二阶无源比例积分取样锁相环的相位误差信号θe的仿真图如图5所示。从图中读出固定环路增益、采样周期与时间常数 τ2改变时间常数 τ1的环路捕获时间相关数据如表1所示。

表1 τ1改变时捕获时间的变化

由表1得出随着时间常数τ1的增大，环路捕获时间会相应地增大，并且τ1越大，环路捕获过程呈振荡型，输出曲线越不平滑。

(2)当固定环路增益、采样周期与时间常数 τ1，改变时间常 数 τ2。 增大 τ2相当于减小 τ1；减小 τ2，相当于增大τ1。所以改变时间常数τ2对无源比例积分取样锁相环特性的影响与改变τ1时是相反的。

2.2 非线性特性与环路增益的关系

当时间常数 τ1、τ2与采样周期 T 固定(τ1=2，τ2=1，T=0.05 s)，改变环路增益 K 分别为 5、10、50、100 时，二阶无源比例积分取样锁相环的相位误差信号θe的仿真图如图6所示。从图中读出固定时间常数与采样周期，改变环路增益的捕获时间，相关数据如表2所示。

表2 K改变时捕获时间的变化

由表2得出随着环路增益K的增大，捕获时间会相应减小；但是当K增大到一定程度后，环路可能进入失锁状态，二阶无源比例积分取样锁相环可能将无法跟踪输入信号。

2.3 非线性特性与采样周期的关系

当时间常数 τ1、τ2与环路增益 K 固定(τ1=2，τ2=1，K=10)，采样周期 T 分别为 0.05 s、0.2 s、0.3 s、0.5 s时，二阶无源比例积分取样锁相环的相位误差信号θe的仿真图如图7所示。从图中读出固定时间常数与环路增益，改变采样周期的捕获时间，相关数据如表3所示。

表3 T改变时捕获时间的变化

由表3可见，随着采样周期T的增大，捕获时间会相应减小，曲线变得越来越不平滑；但是当T增大到一定程度后，捕获时间反而加大，且取样锁相环的稳态相差逐渐增大，系统稳定性能变差，环路可能会进入失锁状态，二阶无源比例积分取样锁相环可能将无法跟踪输入信号。

大量的仿真结果表明，当时间常数、环路增益与采样周期选择合理时，二阶取样锁相环最终都可以锁定输入信号。但是，当三者之中有任何一个发生改变时，都会影响到取样锁相环的非线性特性。

对于二阶无源比例积分取样锁相环，为了快速捕获输入信号，分析如下：

(1)当环路增益与采样周期一定时，应适当减小时间常数 τ1/τ2的比值。

(2)当 τ1/τ2的比值与采样周期一定时，应适当增大环路增益。但也不能过大，以免锁相环进入失锁状态。

(3)当 τ1/τ2的比值与环路增益一定时，应适当增大采样周期。但也不能过大，以免锁相环进入失锁状态。

本文利用Simulink工具箱建立了二阶取样锁相环的相位模型，分析了时间常数、环路增益与采样周期等因素对非线性捕获时间的影响。同时，采用Simulink建模和仿真的方法进行取样锁相环的设计与优化，即方便又灵活，对电子工程设计将达到事半功倍的效果。

[1]SZABO Z，KOLUMBAN G.How to avoid false lock in SPLL frequency synthesizers[J].IEEE Trans.On Instrumentation and Measurement， 2003，52(3)∶927-931.

[2]KOLUMBAN G，VIZVARIB.Nonlinear dynamics and chaotic behavior of the Sampling Phase-locked Loop[J].IEEE Trans.On Instrumentation and Measurement，1994，41(4)∶333-337.

[3]王正林，王胜开.MATLAB/Simulink与控制系统仿真[M].北京：电子工业出版社，2005.

[4]姜占才.二阶锁相环非线性捕获与非线性跟踪性能研究[J].电子科技大学学报，2004，3∶31-34.

[5]张永泰，刘侃，刘洛琨.一种用 MATLAB仿真锁相环的方法[J].无线电工程，2004，34(7)∶47-49.