基于BP算法的无模型自适应迭代学习控制*

李 佳

(青岛科技大学 自动化与电子工程学院 自主导航与智能控制研究所，山东 青岛266042)

针对设计部分依赖、不完全依赖和不依赖受控系统数学模型的控制系统，国内外控制理论界做了多年的努力，发展了许多理论和方法。例如专家系统、模糊控制[1]、神经网络、多模型方法等。最近无模型自适应控制理论得到了广泛的应用，该控制器的设计和分析不需要已知系统的任何知识，仅依赖于系统的输入输出数据，与模型结构、系统阶数均无关。

迭代学习控制(ILC)可利用以前操作的信息修正当前控制行为,提高控制性能，可以实现有限时间区间上的完全跟踪任务，近十几年来得到了广泛的研究[2]。池荣虎将非参数自适应控制（NP-AC）的基本思想和分析手段引入到学习过程中，提出了一种新的无模型自适应迭代学习控制方案（MF-AILC）[3，4]。考虑如下一般非线性离散时间SISO系统：

其中 u(t)和 y(t)分别是系统的输入和输出，t∈{0，1，…T}；ny和 nu表示未知的系统阶数；f(…)表示未知的非线性函数。动态系统式(1)在第k次迭代时的动态方程可表示为：

其中k=0,1,2,…表示系统的迭代次数。对于非线性系统式(2)可以写成如下形式：

其中：

θ(k，t)称为“拟伪偏导数（MPPD）”，是关于过去重复过程中整个时间区间上的所有控制信息的复杂的非线性函数映射，包含了被控对象在过去操作过程的所有控制信号（控制输入和系统输出），即都被融合在 θ(k，t)中。这种控制方案只需系统的输入输出数据，与系统的模型结构、系统阶数无关。

神经网络是借鉴于生物神经网络而发展起来的新型智能信息处理系统，可作为一般的函数估计器，有较强的自学习、自组织与自适应性，能够用数理方法从信息处理的角度对人脑神经网络进行抽象，并建立某种简化模型。模糊逻辑则模仿人脑的逻辑思维机理，用于处理模型未知或不精确的控制问题,对非线性系统控制简单、有效。二者各有所长，具有互补性。模糊神经网络将神经网络与模糊逻辑[5]相结合，这种结合给智能系统提供了一个新的研究方向[6]。

本文在这些研究成果的基础上提出了基于BP算法的神经网络无模型自适应迭代学习控制方案。用该方案寻找一个最佳的“拟伪偏导数”θ(k，t)。该方案只要受控系统的I/O数据，不需要进行系统辩识，同时又具有控制快速性和实时性等优点。仿真表明这样的控制系统能够实现对未知对象的在线控制，并具备适应控制环境变化的能力和自学习的能力[7，8]。

1 基于BP算法的模糊无模型自适应迭代学习控制

给定一个期望的轨迹 yd(t)，t∈{0，1，…，T-1}，使得当迭代次数k趋于无穷时，跟踪误差 e(k，t+1)=yd(t+1)-y(k，t+1)，t∈{0，1，…，T}收敛为零。 据此思想式(3)可写为：

取性能指标函数为：

其中λ1为一个正的权重因子。

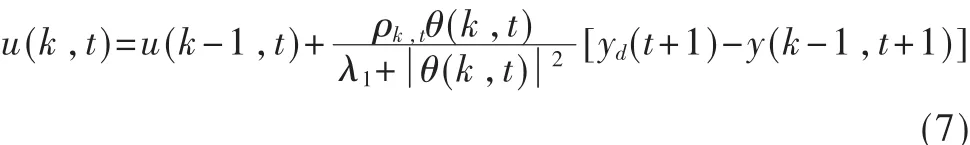
其中 ρk，t为步长序列。事实上，“拟伪偏导数”θ(k，t)是未知不可用的。因此引入BP神经网络算法以及模糊控制方法，对 θ(k，t)进行在线整定。

根据系统的运行状态，调整控制器的参数-拟伪偏导数 θ(k，t)，以达到某种性能指标的最优化，使输出层的输出对应于拟伪偏导数 θ(k，t)，通过神经网络的自身学习、加权系数调整，使其稳定状态对应于某种最优控制律下的无模型自适应控制器的参数。引入模块模糊量化法，系统的状态变量进行归档模糊量化和归一化处理。利用模糊控制的鲁棒性和非线性控制作用，对神经网络NN的输入进行预处理，避免了当神经网络用Sigmoid函数或双曲正切函数时，由于输入过大易导致输出趋于饱和使得对输入不再敏感。

2 算法实现

2.1 BP神经网络

三层BP神经网络，有M个输入节点、Q个隐层节点、一个输出节点，输出节点对应无模型自适应迭代学习控制器的逆为偏导数 θ(k，t)，输出层和隐层的神经元的激励函数可取正负对称的Sigmoid函数。

BP网络的前向计算和加权系数修正迭代算法如下：

输入节点对应经模糊量化处理后的系统状态变量：

Er-j取值为e(r-j)即为r-j时刻系统误差的模糊量化值。M取决于被控系统的复杂程度。

网络的隐含层输出为：

输出层的输出为：

取性能指标函数为：

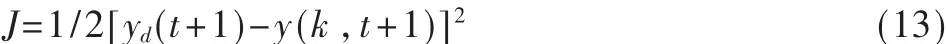
依最速下降法修正网络的加权系数，按J对加权系数的负梯度方向搜索调整，并附加一个使搜索快速收敛到全局极小的惯性项，则有：

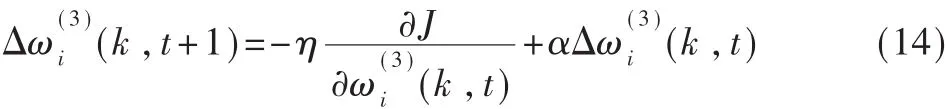
式(14)中，η为学习速率，α为惯性系数。并且有：

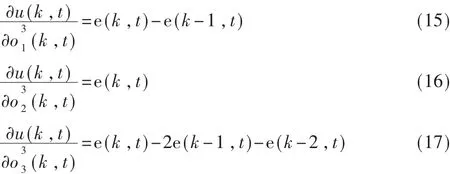
因此可以得BP神经网络NN输出层的加权系数的修正公式为：

依据上述推算办法，可得隐含层加权系数的修正公式：

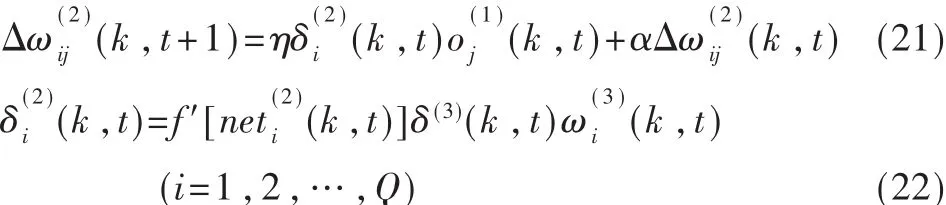
2.2 BP神经网络模糊自适应迭代学习控制算法

基于BP神经网络的无模型自适应迭代控制算法可以归纳为：

(1)选定BP神经网络的结构，给出各层加权系数的初值，选定学习速率和惯性系数，k=1；

(2)采样得到 yd(t)和 y(k，t)，计 e(k，t)=yd(t)-y(k，t)；

(3)根据式（8）对 e(k，t)进行模糊化处理，作为 BP 网络的输入；

(4)根据式(9)～式(13)计算前向 BP网络的各层神经元的输入和输出，NN输出层的输出即为控制器的参数 θ(k，t)；

(5)根据 θ(k，t)由式(7)计算无模型自适应迭代学习控制的控制输出u(k，t)；

(6)由式(14)～式(22)计算输出层和隐含层的加权系

3 仿真研究

考虑非线性系统

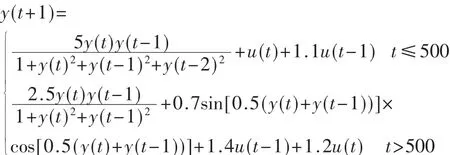
该系统结构、阶数均时变，且系统具有非最小相位特性。系统要跟踪的目标轨迹为：

系统初值设置为：u(1)=u(2)=0，y(1)=-1，y(2)=1，y(3)=0.5，逆伪偏导数 θ(1)=2，λ=2，ρ=0.6。 采用 BP 神经网络无模型自适应迭代学习控制方案，BP神经网络NN的结构为 3-8-1，即 M=3，Q=8。从图 1所示的仿真可以看出该控制方案有较好的跟踪性能。

本文将BP神经网络、模糊理论及无模型自适应迭代学习相结合，构造出了一种基于BP神经网络的模糊无模型自适应迭代学习控制器。该控制器综合了三者的优点，利用有着较强的非线性逼近性的BP神经网络学习逆伪偏导数。文章提出的控制方案，不需要已知系统的任何先验知识，是一种无模型的方法，而且迭代学习控制律的学习增益仅依赖于系统的输入输出数据设计，并可沿学习轴迭代地更新。仿真结果表明了该控制方案的有效性。

[1]李友善.Fuzzy控制理论在甜菜制糖过程的应用[J].自动化学报,1994,20(3)：334-337.

[2]LIN C J,LIN C T.An ART-based fuzzy adaptive learning control networks[J].IEEE Trans on Fuzzy Systems，1997,5(4):477-496.

[3]池荣虎.非线性离散时间系统的自适应迭代学习控制及应用[D].北京：北京交通大学博士论文，2006.

[4]CHI Rong Hu,HOU Zhong Sheng.A model-free adaptive control approach for freeway traffic density via ramp metering[J].IJICIC 2008，4(11):2823-2832.

[5]刘有才,刘增良.模糊逻辑与神经网络[M].北京：北京航空航天大学出版社,1996.

[6]ZHANG Jin,LI Heng Tong.Adaptive neural network control for a class of MIMO nonlinear systems with disturbances in discrete-time[J].IEEE Trans on Fuzzy Systems,2004,34(4).

[7]施阳.MATLAB语言精要及动态仿真工具SIMULINK[M].西安：西北工业大学出版社,1999.

[8]闻新,周露,李翔,等.MATLAB神经网络仿真与应用[M].北京：北京科学出版社,2003.