外视场拼接测量系统的视场拼接和交汇测量算法及其实现

王 旻，宋立维，乔彦峰，余 毅

（1.中国科学院长春光学精密机械与物理研究所，吉林 长春 130033；2.中国科学院研究生院 北京 100039）

外视场拼接测量系统的视场拼接和交汇测量算法及其实现

王 旻1，2，宋立维1，乔彦峰1，余 毅1

（1.中国科学院长春光学精密机械与物理研究所，吉林 长春 130033；2.中国科学院研究生院 北京 100039）

基于2台外视场拼接高速电视测量仪原型样机（硬件）提出了一种将交汇测量和拼接处理相结合的算法。根据需要对地球质心和光电测量系统建立了5个坐标系，介绍了坐标系的定义及其它们之间的变换过程，给出了目标轨迹交汇测量和视场拼接的实例。用2台高速电视测量仪拼接的8台测量相机同时对同一运动目标进行测量，对获得的测量数据进行交汇和视场拼接处理，结果显示提出的拼接算法是正确、有效的，可以得到唯一解；地球曲率半径和地球子午线收敛两项影响因素得到了完全修正，表明交汇测量算法完全可以推广到其它光电测控仪器的交汇测量。

外视场拼接；交汇测量；地球曲率半径；子午线收敛；误差修正

1 引言

在目标高速测量领域，被测目标速度快、目标多、所占的视场范围大，应用单台的高速摄像机不能拍摄到完整的画面。为了克服单台相机拍摄的不足，研制了一种将4台高速相机拼接为1台高速电视测量仪的方法，实现了对多个目标的完整拍摄。本文基于2台外视场拼接高速电视测量仪原型样机（硬件），提出了一种将交汇测量和拼接处理相结合的算法。用2台高速电视测量仪拼接的8台测量相机同时对同一运动目标进行测量，对获得的测量数据进行交汇和视场拼接处理。结果显示，提出的拼接算法是正确、有效的，可以得到唯一解；地球曲率半径和地球子午线收敛两项影响因素得到了完全修正，表明提出的交汇测量算法，完全可以推广到其它光电测控仪器的交汇测量。

2 外场拼接原理

外视场拼接测量系统，一般由3个测量站光电测量仪组成，首先通过2台以上的光电测量仪测得的数据进行交汇计算，获得每个目标在空间的三维位置信息，然后进行视场拼接［1，2］。采用外视场拼接，光学系统简单、重量轻、体积小、制造难度低，便于使用，但由于外视场拼接不可避免存在视差，因此进行视场拼接时，计算量大。近代计算机技术的发展，给外视场拼接提供了可能。如图1所示的配置，每个测量站光电测量仪上安装4个测量相机，这4个测量相机上下、左右对称地配置在“T”字型跟踪架水平轴外伸两轴端，组成“田”字型布局配置，即为较典型的外视场拼接测量系统。4台摄像机视场在外视场呈水平方向“一”字拼接，且采用凝视工作模式。

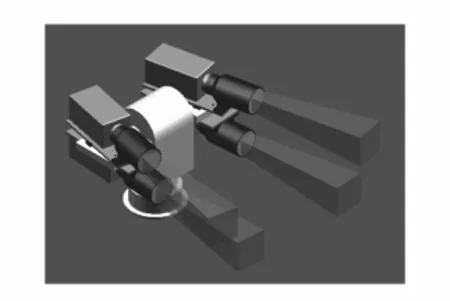
图1 外视场拼接测量系统的外观图Fig.1 Outlook of external field butting measuring system

由于各光电测量仪的4个测量相机在上下、左右方向都存在视差，在目标没有距离信息的情况下，只依靠单台光电测量仪的信息不可能完成精密视场拼接，只有应用两台光电测量仪所获得的信息，对同一目标同时进行视场拼接和交汇测量，才能完成精密的视场拼接。

考虑采用“T”字型跟踪架［3］，“田”字型布局配置的光电测量仪，4个测量相机在上下、左右方向都存在视差，其视场拼接和交汇测量的数学模型具有典型性，本文对这一方案进行了分析，并以一个目标为例，建立了视场拼接和交汇测量的数学模型，在建立数学模型时，考虑了地球曲率半径和子午线收敛误差的影响［4，5］。

3 坐标系定义

根据实际分析的需要共建立5个坐标系［6～8］（见图2）。各坐标系（右手坐标系）定义如下：

（1）地球质心坐标系I（i1，i2，i3）；

（2）第i个光电测量仪地平坐标系Si（si1，si2，si3）；

（3）第i个光电测量仪垂直轴坐标系Vi（vi1，vi2，vi3）；

（4）第i个光电测量仪水平轴坐标系Hi（hi1，hi2，hi3）；

（5）第i个光电测量仪、第j个测量相机坐标系Cij（cij1，cij2，cij3）。

图2 外视场拼接测量系统在地心质心坐标系中的坐标系统示意图Fig.2 Coordinates of external field stitchingmeasuring system in earth centroid coordinate

4 测量相机外视场拼接参数ξij的确定

用文中4个测量相机的配置方式进行外视场拼接时，不可避免地会造成视差。当拼接参数ξij选择不当时，在一定的测量距离上会产生测量盲区（即漏测），或者浪费测量相机的视场资源。为了实现每台光电测量仪的4个测量相机视场在外场的合理拼接，可以让中间的两个（第二个和第三个）测量相机之间，在0.7l1距离处的外视场紧密拼接（确保不露缝），而在两边的两个（第一个和第二个、第三个和第四个）测量相机之间为紧密搭接（即视场边缘的像元既无重叠又无间隙，条件是第一和第二个，第三和第四个测量相机的节点，上下对齐）。如图3所示。

由图3所示的几何关系可知：

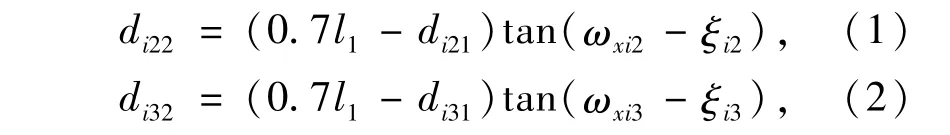
由此可解得ξi2和ξi3，并进一步解得ξi1和ξi4：

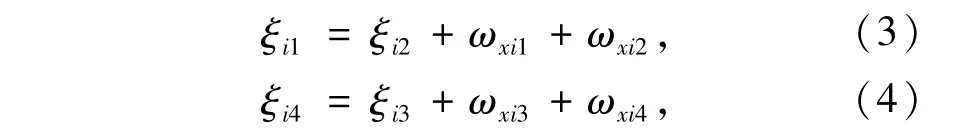
式中l1为被测量目标到光电测量仪地平坐标系原点Si的最近距离；ξij为第i个光电测量仪，第j个测量相机光轴，相对第i个光电测量仪水平轴坐标系在方位上的偏转角；dij1、dij2、dij3为第i个光电测量仪，第j个测量相机望远镜头的节点，相对第i个光电测量仪水平轴坐标系原点Hi，在3个坐标轴上的位移距离；ωxij、ωyij分别为第i个光电测量仪，第j个测量相机在横向和竖向的半视场角。

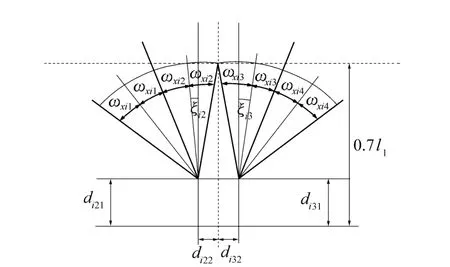
图3 测量相机排列示意图Fig.3 Sketch of cameras ordering

为了使各测量相机的各视场之间有一定的覆盖，计算时可将各相机的有效视场角减小一定的量值，用来实现视场的覆盖。

5从第i个光电测量仪，第j个测量相机坐标系到第i个光电测量仪水平轴坐标系Hi（hi1，hi2，hi3）的变换

设第k个目标到第i个光电测量仪，第j个测量相机坐标系Cij原点的距离为rijk，则该目标在第i个光电测量仪，第j个测量相机坐标系Cij中的测量值Cijk为：

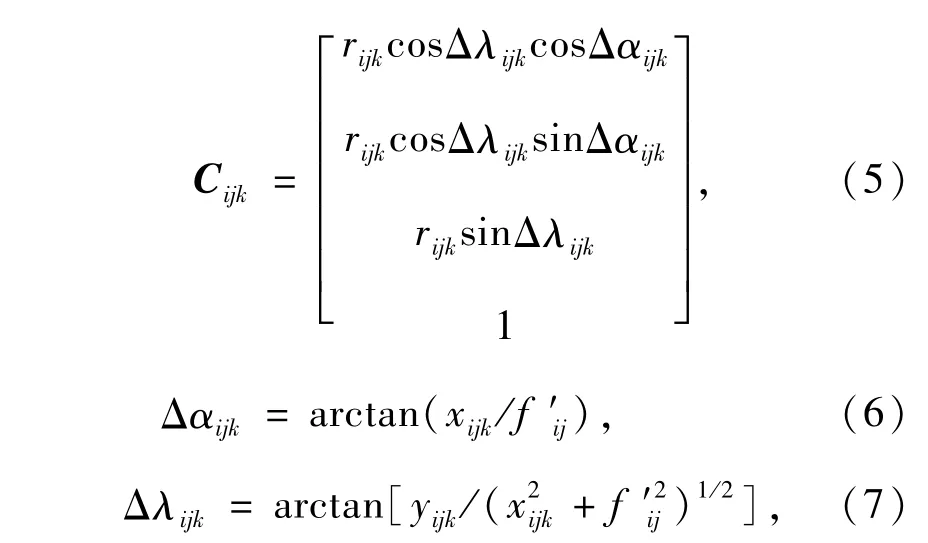
式中，k为被测目标的序号；Δαijk、Δλijk分别为第k个目标，在第i个光电测量仪，第j个测量相机坐标系中的方位角和俯仰角；xijk、yijk分别为第i个光电测量仪，第j个测量相机的面阵CCD上，第k个目标的横向和竖向脱靶量（mm）；f′ij为第i个光电测量仪，第j个测量相机镜头的焦距（mm）。

设第k个目标到第一个光电测量仪，第j个测量相机坐标系C1j原点的距离为r1jk，则该目标在第一个光电测量仪第j个测量相机坐标系C1j中的测量值C1jk为：

其中，

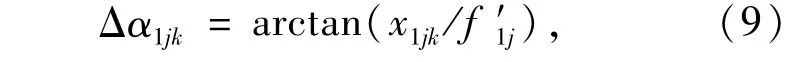
设第k个目标经过视场拼接后，在第i个光电测量仪水平轴坐标系Hi（测量相机视场拼接后的组合测量相机坐标系）中，测量值Hik为：

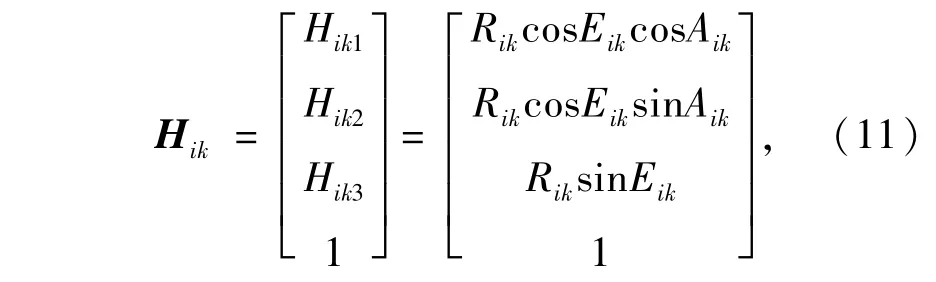
式中Rik为第k个目标到第i个光电测量仪，水平轴坐标系Hi原点Hoi的距离；Aik、Eik分别为第k个目标在第i个光电测量仪水平轴坐标系中的方位角和俯仰角。

经如下的坐标转换过程：

（1）绕cij3轴旋转（-ξij）角；

（2）沿cij1轴平移（-dij1）；

（3）沿cij3轴平移（-dij3）；

（4）沿cij2轴平移（-dij2），

可以实现第k个目标，在第j个测量相机坐标系Cij中的测量值到第i个光电测量仪水平轴坐标系Hi中测量值的变换。

同理应用下述的坐标转换过程：

（1）绕ci13轴旋转（-ξi1）；

（2）沿ci11轴平移（-di11）；

（3）沿ci13轴平移（-di13）；

（4）沿ci12轴平移（-di12），

可以实现第k个目标，在第一个测量相机坐标系Ci1中的测量值，到第一个光电测量仪水平轴坐标系H1中的测量值的变换：

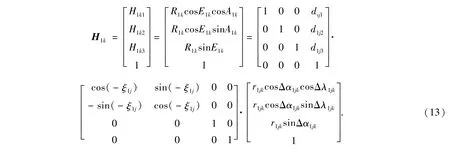
6从第i个光电测量仪水平轴坐标系到第一个光电测量仪水平轴坐标系的变换，即Hi（hi1、hi2、hi3）到H1（h11、h12、h13）的变换

经如下的坐标转换过程：

（1）从第i个光电测量仪水平轴坐标系Hi到第i个光电测量仪垂直轴坐标系Vi的坐标转换：①绕hi2轴旋转-λi角；

（2）从第i个光电测量仪垂直轴坐标系Vi到第i个光电测量仪地平坐标系Si的坐标转换：②绕si3轴旋转-αi角；

（3）从第i个光电测量仪地平坐标系Si到地球质心坐标系I的坐标转换：③沿si3轴平移-hi；④绕si2轴旋转-θi角；

（4）从地球质心坐标系I到第1个光电测量仪地平坐标系S1的坐标转换：⑤绕i1轴旋转δiδ1角；⑥绕i2轴旋转θ1角；⑦沿S13轴平移h1；

（5）从第1个光电测量仪地平坐标系S1到第1个光电测量仪垂直轴坐标系V1的坐标转换：⑧绕s13轴旋转α1角；

（6）从第1个光电测量仪垂直轴坐标系V1地平坐标系S1到第1个光电测量仪水平轴坐标系H1的坐标转换：⑨绕v12轴旋转λ1角。

可以实现第k个目标，在第i个光电测量仪水平轴坐标系中的测量值Hik，到第一个光电测量仪地平坐标系H1中的测量值H1k的变换：

式中：δi、θi、hi为第i个光电测量仪坐标系原点Soi处的赤经、赤纬和相对地球质心的高程（单位km）；αi为第i个测量站光电测量仪垂直轴坐标系与地平坐标系（正北方向N）之间的夹角（即真方位角）；λi为第i个测量站光电测量仪水平轴坐标系相对垂直轴坐标系的俯仰角。

7 交汇测量和视场拼接结果

7.1 交汇测量结果

由于每台光电测量仪的4台测量相机之间都存在左右和上下的视差，仅仅应用测量相机的测量数据不可能完成在自身的光电测量仪中的视场拼接。如式（5）和（8）所示，要完成视场拼接首先应解出距离rijk和r1jk，也就是说首先要对2台光电测量仪的测量相机的测量数据进行交汇［9～13］，求得距离信息rijk和r1jk，即通过联解方程组（15）、（16）求得rijk和r1jk。其中式（15）由式（12）和式（14）联立而得；式（16）即式（13）。

7.2 视场拼接结果

通过解方程（12）可求出Rik，Eik和Aik，则在第i个光电测量仪中，视场拼接后第k个目标在第i个光电测量仪水平轴坐标系中（即视场拼接后在组合视场中）的测量值Hik为：

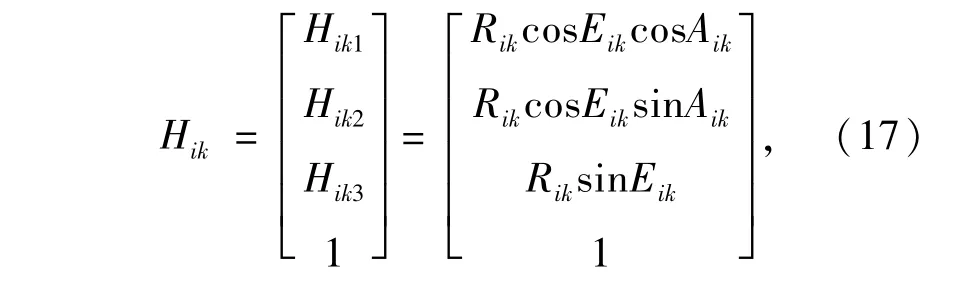
由于：

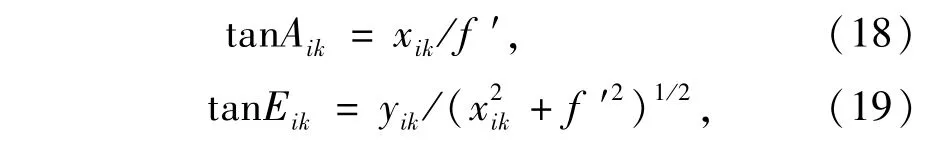
式中f′为测量相机视场拼接后的组合测量相机的标准镜头焦距（mm）；xik，yik分别为在第i个光电测量仪中，经视场拼接后，第k个目标在第i个光电测量仪组合测量相机视场中的横向和竖向脱靶量（mm）。

由此可得第k个目标在第i个光电测量仪中，视场拼接后在组合视场中两个方向上的脱靶量xik和yik为：

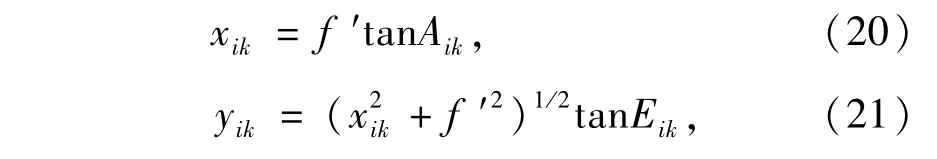
通过解（13）可求出R1k，E1k和A1k，则在第1个光电测量仪中，第k个目标在第1个光电测量仪水平轴坐标系中（即视场拼接后在组合视场中）的测量值H1k为：

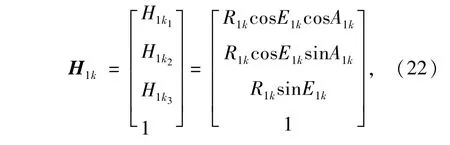
由于：

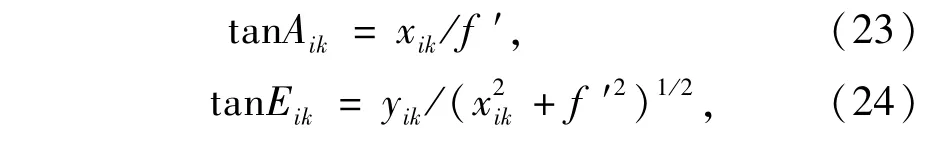
可得第k个目标在第1个光电测量仪中经视场拼接后在组合视场中两个方向上的脱靶量x1k和y1k为：

8 被测目标轨迹的交汇测量和视场拼接实例

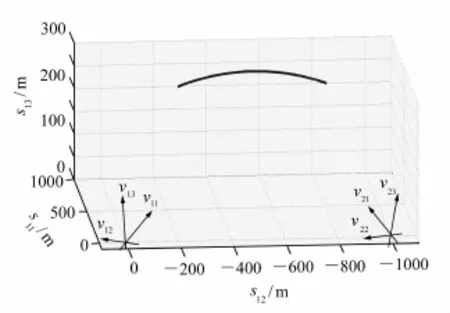
图4 测量站1、2的地平坐标系，以及目标轨迹在测量站1地平坐标系中的三维图Fig.4 Target path in geodetic coordinates atmeasurement station 1，and the geodetic coordinates at measurement station 1 and 2

如图4所示，图中以测量站1的地平坐标系为基准，分别示出了测量站1、2的地平坐标系，以及目标在测量站1地平坐标系中的三维轨迹。

测量站1和2的地平坐标系参数为：

δ1＝125.35°、θ1＝43.88°、h1＝6 371 000m；

δ2＝125.362 5°、θ2＝43.88°、h2＝6 371 005m。

测量站1和2的电视测量仪水平轴坐标系（即组合视场1和2光轴）在各自地平坐标系中的方位和仰角参数为：α1＝-35°、λ1＝15°；α2＝30°、λ2＝15°。

因为拟测目标区域与测量站之间的最短距离为500m，也就是说大于500m距离，被测目标可实现无盲区覆盖，本文采用l1＝500m进行拼接参数设计。

由已知电视测量仪的下列结构参数：

d111＝d121＝d131＝d141＝0mm；

d211＝d221＝d231＝d241＝0mm；

d112＝d122＝d212＝d222＝430mm；

d132＝d142＝d232＝d242＝-430mm；

d113＝d143＝d213＝d243＝180mm；

d123＝d133＝d223＝d233＝-180mm；

f′11＝f′12＝f′13＝f′14＝94mm；

f′21＝f′22＝f′23＝f′24＝94mm；

ωxij＝4.98°、ωyij＝4.98°，

根据公式（1）、（2）、（3）、（4），得出电视测量仪1和2的其它结构参数为：

ξ12＝ξ22＝4.9096°；

ξ11＝ξ21＝14.8696°；

ξ13＝ξ23＝-4.9096°；

ξ14＝ξ24＝-14.8696°。

图5和图6分别为在测量站1和2处的两个高速电视测量仪的8台测量相机C11，C12，C13，C14和C21，C22，C23，C24，用500frame/s的采样频率，对同一运动目标在视场中获得的测量值，总测量时间为2s，总采样数据为1 000组。

图7和图8分别为根据测量站1和2的2个高速电视量仪的8台测量相机对在视场中获得的同一运动目标测量值进行交汇测量处理和视场拼接后在电视测量仪中拼接视场中的拼接结果（轨迹）。

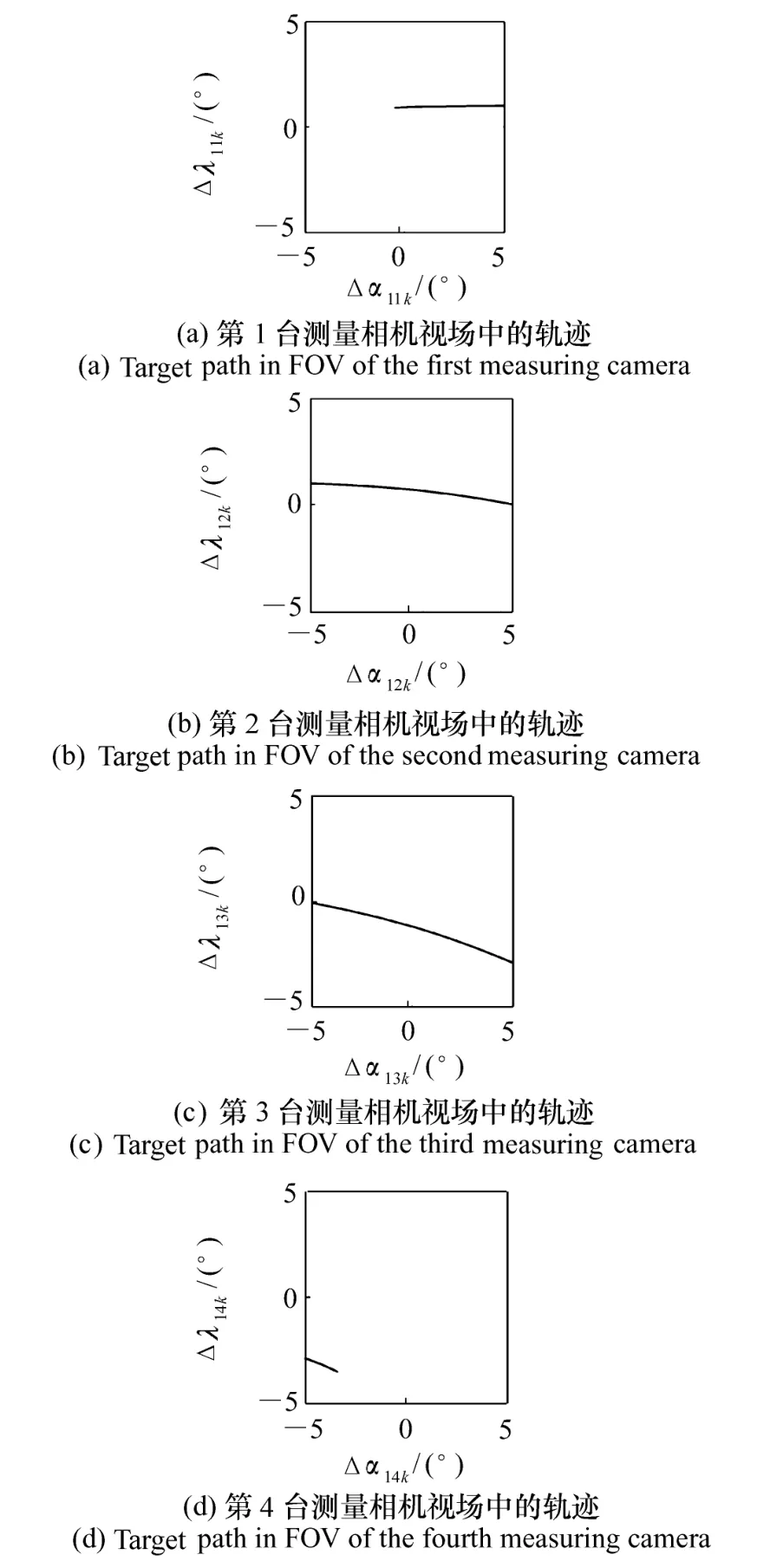
图5 运动目标在测量站1中C11、C12、C13、C144个测量相机视场中的轨迹Fig.5 Target paths in FOV of C11，C12，C13，C14 at measurement station1

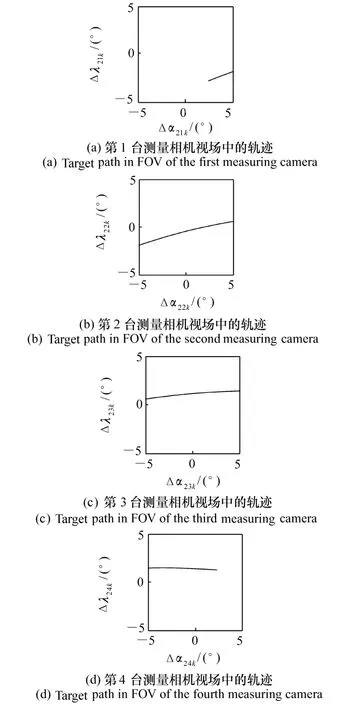
图6 运动目标在测量站2中C11、C12、C13、C144个测量相机视场中的轨迹Fig.6 Target paths in FOV of C11、C12、C13、C14 at measurement station 2

图7 运动目标在测量站1拼接视场中的轨迹Fig.7 Target path in FOV after field stitching ofmeasurement station 1

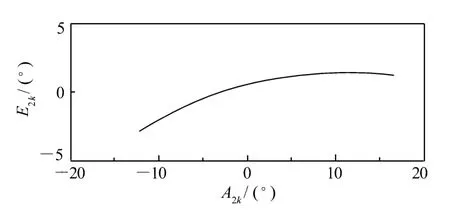
图8 运动目标在测量站2拼接视场中的轨迹Fig.8 Target path in FOV after field stitching ofmeasurement station 2

9 结论

能否实现高速电视测量仪外视场拼接，取决于硬件和拼接算法（软件）两个方面。本文在2台高速电视测量仪原型样机（硬件）研制成功的基础上，提出了一种将交汇测量和拼接处理相结合的算法，通过用2台高速电视测量仪的8台测量相机测量同一运动目标，并对获得的测量数据进行交汇和视场拼接处理，得出以下结论：

（1）拼接算法是正确、有效的，可以得到唯一解。（2）要完成视场拼接，首先要根据交汇测量原理，对数据进行交汇测量处理［9～13］，解出目标的距离信息。（3）本文中提供的交汇测量拼接算法，由于引入地球质心坐标系变换，地球曲率半径和地球子午线收敛角两项影响因素得到了完全修正（当两站测量仪在同一纬度上时，两个站点之间的地球子午线收敛角最大，设两个站点测量仪在纬度为43.88°，相距1km时，其地球子午线收敛角约为45″，两站地平面铅垂线之间的夹角约为32.5″）。（4）本文中的交汇测量算法，完全可以推广到其它光电测控仪器的交汇测量，如果拟测量的目标越远，或测量站间布站距离越大，则这种算法的效果和优点就更明显。（5）视场拼接和交汇测量的总误差，主要来自两个方面：一是光电测量仪本身的测量误差；二是布站点处地平坐标系原点位置的测量误差。外视场拼接和交汇测量算法本身不引入误差。

需要注意的是，布站时任意2台光电测量仪到被测目标区域之间的夹角不要过小，最好符合正交布站原则，否则由于光电测量仪本身的测量误差和布站点位置测量误差的影响，会导致交汇测量误差增大，甚至造成交汇无解。

［1］刘罡，高晓东，曹学东.大视场光电测量系统实时测量精度的综合标定［J］.光电工程，2001，28（6）：10-13.

LIU G，GAO X D，CAO X D.A comprehensive calibration of the real-time measurement accuracy for a photoelectrical measuring system with wide field of view［J］.Opto-electronic Eng.，2001，28（6）：10-13.（in Chinese）

［2］于晓波，盛磊.靶场测量中多镜头大视场视频图像的拼接［J］.光学精密工程，2008，16（11）：2145-2150.

YU X B，SHENG L.Image stitching of multi-lens with large visual field in range instrumentation［J］.Opt.Precision Eng.，2008，16（11）：2145-2150.（in Chinese）

［3］贾峰，李桂芝，南雪飞.靶场T型架光电经纬仪精度检测方法的研究与应用［J］.飞行器测控学报，2007，26（2）：24-29.

JIA F，LIG ZH，NAN X F.An accuracy testmethod for type-T cinetheodolites in instrum entation ranges［J］.J.Spacecraft TT＆C Technol.，2007，26（2）：24-29.（in Chinese）

［4］何照才，胡保安.光学测量系统［M］.北京：国防工业出版社，2002.

HE ZH C，HU B A.Optical Measure Systems［M］.Beijing：National Defence Industry Press，2002.（in Chinese）

［5］赵学颜，李迎春.靶场光学测量［M］.北京：国防工业出版社，2001.

ZHAO X Y，LIY CH.Optical Measure at Shooting Range［M］.Beijing：National Defense Press，2001.（in Chinese）

［6］王家骐.光学仪器总体设计［M］.长春：中科院长春光学精密机械与物理研究所，2003.

WANG JQ.Optical Instrument Collectivity Design［M］.Changchun：Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，2003.（in Chinese）

［7］金光，王家骐.利用坐标变换推导经纬仪三轴误差［J］.光学精密工程，1999，7（5）：89-94.

JIN G，WANG JQ.The three-error axis of theodolitewith the utilization of the coordinate to the variation［J］.Opt.Precision Eng.，1999，7（5）：89-94.（in Chinese）

［8］王家骐，金光，颜昌翔.机载光电跟踪测量设备的目标定位误差分析［J］.光学精密工程，2005，13（2）：105-116.

WANG JQ，JIN G，YAN CH X.Orientation error analysis of airborne opto-electric tracking and measuring device［J］.Opt.Precision Eng.，2005，13（2）：105-116.（in Chinese）

［9］冯桂兰，田维坚，屈有山，等.实时视场拼接系统的设计与实现［J］.光电工程，2007，34（4）：124-127.

FENG G L，TIAN W J，QU Y SH，et al..Design of real-time video mosaic system［J］.Opto-electronic Eng.，2007，34（4）：124-127.（in Chinese）

［10］任建岳，孙斌，张星祥，等.TDICCD交错拼接的精度检测［J］.光学精密工程，2008，16（10）：1852-1857.

REN JY，SUN B，ZHANG X X，et al..Precision measurement of TDICCD interleaving assembly［J］.Opt.Precision Eng.，2008，16（10）：1852-1857.（in Chinese）

［11］兰海滨，王平，龙腾.图像拼接中相机镜头非线性畸变的校正［J］.光学精密工程，2009，17（5）：1196-1202.

LAN H B，WANG P，LONG T.Nonlinear aberration correction of lens in imagemosaic［J］.Opt.Precision Eng.，2009，17（5）：1196-1202.（in Chinese）

［12］李喆，丁振良，袁峰.基于共面点的多视觉测量系统的全局标定［J］.光学精密工程，2008，16（3）：467-472.

LIZH，DING ZH L，YUAN F.Global calibration method formulti-vision measurement system with coplanar targets［J］.Opt.Precision Eng.，2008，16（3）：467-472.（in Chinese）

［13］费业泰.误差理论与数据处理［M］.北京：机械工业出版社，2007.

FEIY T.Error Theory and Data Processing［M］.Beijing：China Machine Press，2007.（in Chinese）

Convergence algorithm of field stitching and intersection measurement for external field stitching measuring system and its im plementation

WANG Min1，2，SONG Li-wei1，QIAO Yan-feng1，YU Yi1
（1.Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033，China；2.Graduate University of Chinese Academy of Sciences，Beijing 100039，China）

A convergence algorithm of field stitching and intersection measurement is proposed based on the development of two prototypes of high-speed video-measuring systemswith external field stitching.Five coordinates are established for the earth centroid and optoelectronical systems.The definations of the coordinates are introduced and coordinate transforms are discussed.The experiment of intersection measurement and field stitching for an identicalmoving target is carried out with the data from eight cameras in two high-speed TV measuring instruments.The result shows that the stitching algorithm is correct and effective，and has obtained an unique solution.Meanwhile，the influences of earth curvature and meridional convergent errors are fullycorreated，which indicates that the intersection measurement algorithm can also be used in the intersection measurement of other optoelectronicalmeasurement and control instruments.

external field stitching，intersection measurement，earth curvature，meridional convergence；error correction

1674-2915（2010）03-0229-10

V557.3；TP391.4

A

2010-03-12；

2010-04-13

王 旻（1977—），女，吉林长春人，硕士研究生，主要从事光电瞄准与测量的研究。E-mail：work6180@yahoo.com.cn

乔彦峰（1962—），男，吉林长春人，研究员，博士生导师，主要从事光电测量与控制技术方面的研究。E-mail：qiaoyf@ciomp.ac.cn