基于马尔可夫链的EWMA控制图参数优化及其实现
2010-05-11白双梅杜福洲
白双梅,杜福洲
(北京航空航天大学 机械工程及自动化学院,北京 100191)
基于马尔可夫链的EWMA控制图参数优化及其实现
白双梅,杜福洲
(北京航空航天大学 机械工程及自动化学院,北京 100191)
0 引言
SPC是一种借助数理统计理论的过程质量控制方法,通常采用控制图来达到过程控制的目的。
传统的休哈特控制图的统计变量只与当前观测值相关,而忽略大量过程历史数据中包含的信息,因此,传统的休哈特控制图对小偏移过程不敏感,往往会造成漏判情况的出现。为此,研究者们提出了累积和(CUSUM)控制图和指数加权滑动平均(EWMA)控制图来实现对小偏移过程的监控。
EWMA控制图的性能取决于参数(平滑系数λ、控制线参数L)的选取,因此,EWMA控制图参数的选取直接影响控制图对小偏移过程的控制效果。有关控制图参数优化问题日益引起广泛关注,相关研究人员曾提出以田口质量损失函数最小为目标的CUSUM控制图优化设计方法,应用马尔可夫链研究了多元指数移动平均控制图及MCUSUM控制图中ARL计算的数学模型[1~3],设计监控EWMA控制图均值和方差的经济控制图[4],在文献[5]中基于马尔可夫链法对EWMA控制图参数优化算法进行了研究。
学术界和实际应用中常用平均运行链长(average run length,ARL)作为控制图性能评价指标。运行链长(run length,RL)是对给定的质量水平、控制图从开始应用到发出报警所抽取的样本数,为随机量,其分布状况可以作为控制图应用的决策依据。ARL是RL的期望值,理想控制图的特点是:过程受控时,ARL值尽可能大;过程失控时,ARL值尽可能小。目前,常用的ARL计算方法有三种,即蒙特卡罗仿真法、积分法、马尔可夫链法。基于马尔可夫链法的EWMA控制图ARL计算算法原理是:将EWMA控制图的上下控制线之间的区间分成k(k为奇数)个子区间,将EWMA控制图绘制的过程近似看成一个离散的马尔可夫链(k的取值越大,该过程越近似于马尔可夫链,则ARL可以用转移概率矩阵表示。
本文在现有研究成果的基础上,系统地研究了基于马尔可夫链的EWMA控制图参数优化方法,基于matlab进行仿真验证,总结出具体的EWMA控制图参数优化步骤,并基于J2EE平台实现EWMA控制图参数优化系统,进而与传统的控制进行了比较研究。
1 EWMA控制图
设X,N(μ0,σ02)其中μ0和σ02分别是过程处于受控状态时的均值和方差。X1,X2,L,Xn(n为样本容量),是相互独立的随机变量序列,其中Xi为第i个样本值,则EWMA统计量为:


由式(2)可见,距离当前越远的数据,权重越小,以指数形式递减。
根据上述模型及六西格玛原则,EWMA控制图上、下控制限UCL和LCL,分别为[5]:

式中,n为样本容量,λ为平滑系数,L为确定控制线的参数。由此可见,平滑系数λ及控制线参数L的选取是影响EWMA控制图对小偏移控制的重点因素。
2 基于马尔可夫链的ARL计算方法
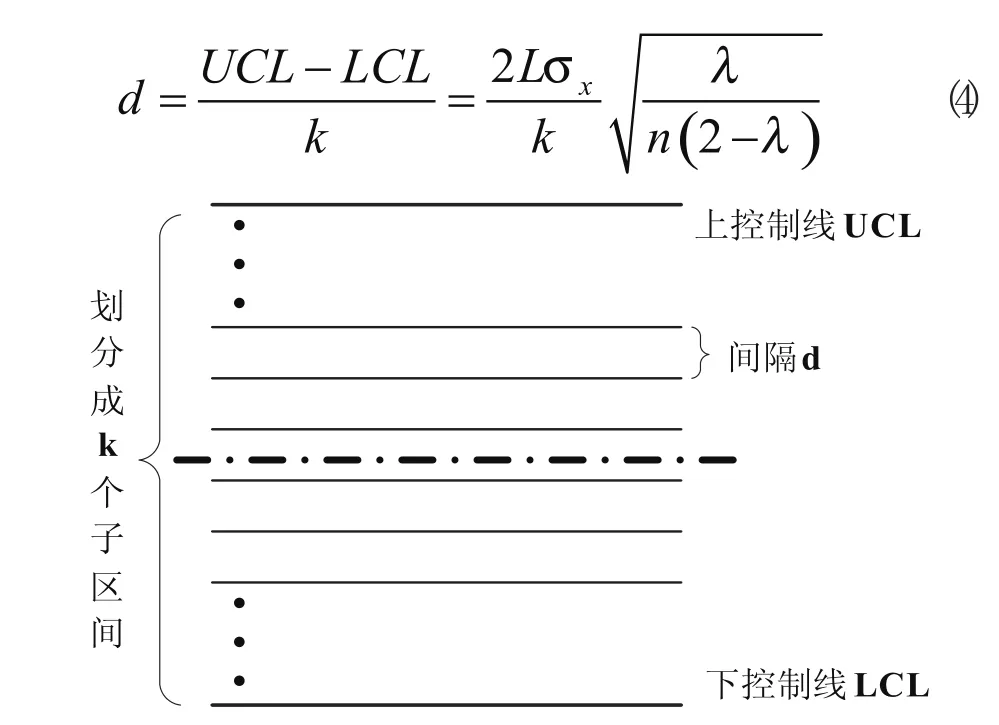
图1 马尔可夫链状态空间划分示意图
将EWMA控制图绘制的过程近似看成一个离散的马尔可夫链(k的取值越大,该过程越近似于马尔可夫链),用Si(i=1,2,…,k)表示该马尔可夫链的状态,且设Si为子区间的中心点,则

统计量zi落在控制限之外的状态表示为Sa,Si假设zi一旦超出控制限不会自动返回,则Sa为一个吸收态。这样整个EWMA的监控过程就可以描述为带有一个吸收壁的马尔可夫链。该马尔可夫链的一步转移概率矩阵P可表示为

式中,R为k×k矩阵,表示从转移状态Si到转移状态Sj的概率Pij(i=1,2,…,k)。I为k×k单位矩阵,1为所有元素均为1的k×1列向量,0为所有元素均为0的k×1列向量。Pij可表示为:

由马尔可夫链的定义,第i步转移概率矩阵Pi可表示为

则链长PL=i的概率可以表示为

式中,Pinitial为初始状态概率,为简单起见设恒从中心点出发,因此

3 EWMA控制图参数优化算法
基于上述计算EWMA控制图ARL的数学模型,总结了EWMA控制图参数优化算法。
EWMA控制图参数优化算法流程如图2所示:

图2 EWMA控制图参数优化算法流程
对于给定参数(λ,L)的EWMA检验方案来说,对过程的不同质量水平进行检验,其效果表现在它的ARL值。反之,对于一个具有不同质量水平的过程来说,其效果表现在给定受控平均运行链长值(ARL0)的情况下,能推导出适合的检验方案(λ,L)。
在进行EWMA控制图的设计时,参数λ和L的选取至关重要。基于ARL的EWMA控制图参数(λ,L)优化算的一般步骤如下:
1)先确定参数:置信度α、样本容量n、欲控过程偏移量δ、标准差σ、马尔可夫链区间划分数k、控制线参数变化范围LN,并计算出ARL0;
2)然后,计算满足ARL0的几组(λ,L)值对,拟合λ与L的回归曲线;
3)拟合λ、L的回归方程,以一定间隔取得(λ,L)值对;
4)根据(λ,L)值对及给定参数,计算取该参数时的ARL值;
5)计算ARL与λ的回归方程,寻找ARLmin,从而得到优化参数(λ0,λ0)。
基于ARL的EWMA控制图参数选取的方法是:在ARL0已定的前提下,即控制图的置信度已知,选取参数(λ,L)使得ARL1越小越好。
4 基于matlab的EWMA控制图参数优化
由前面基于马尔可夫链的EWMA控制图ARL的计算方法的研究可知,随着区间划分数k的增加,EWMA控制图绘制过程越来越趋向于马尔可夫链过程;为验证算法的稳定性,取k从10到190,步长为4(δ=0.2,λ=0.2,L=2.7),基于matlab仿真ARL曲线如图3所示。
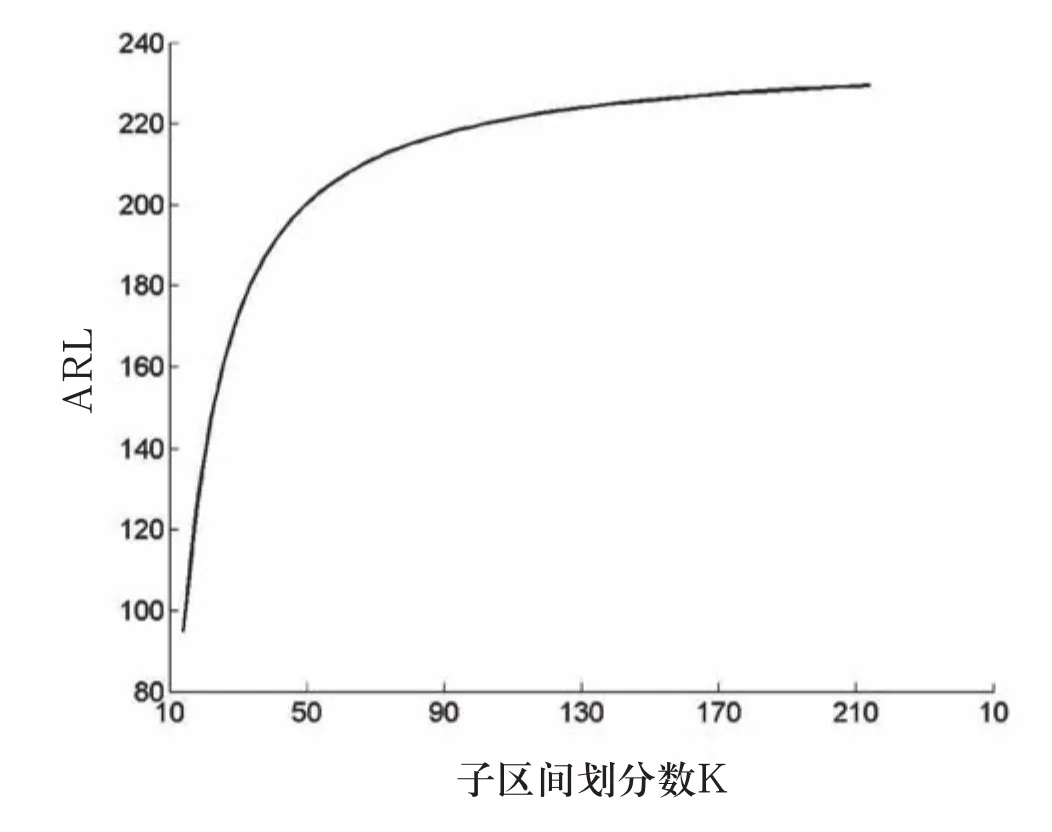
图3 子区间划分数对ARL计算结果的影响
随着k的增加,ARL极限存在,由此可知,此过程可收敛。
下面研究EWMA控制图参数对其过程控制的影响。
首先,研究不同控制线参数L(λ=0.23、k=50)下的EWMA控制图操作特性(operation characteristic,OC)曲线,观查控制线参数L对控制效果的影响,如图4所示。
由曲线图可见,L越大,ARL0越大,表示过程受控时误判的概率越低。随着偏移量δ增大,ARL呈下降趋势,但L越大,ARL越大,也就意味着当过程失控(δ>0)时,漏判的概率随L的增大
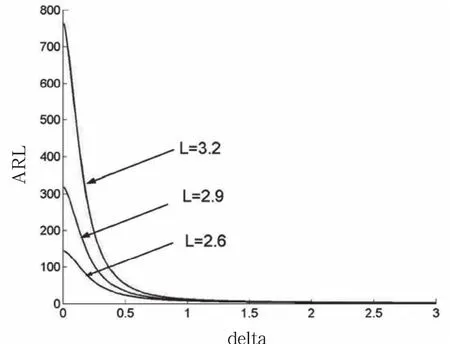
图4 控制线参数 对EWMA控制图OC曲线的影响

图5 不同平滑系数λ下的EWMA控制图OC曲线
由图5可见,取不同平滑系数λ时, OC曲线存在交点δ∗和δ∗∗。δ=0时,λ越小,控制图性能越优。0<δ<δ∗之间,λ越大,控制图性能越优。δ∗<δ<δ∗∗时,随λ的减小控制图性能变好;δ>δ∗∗时,控制图的性能趋同。
5 EWMA控制图参数优化实例
根据第4部分的结论,EWMA控制图的性能与控制线参数L、平滑系数λ以及过程均值偏移量δ相关。显然,需要根据过程均值波动的不同,选择不同的参数。下面根据具体案例演示控制图参数优化系统界面及优化参数选取过程。
在轴的车削加工过程当中,由于温度升高以及磨损等原因导致刀具迸刀,因而轴的直径发生了小偏移,假设偏移量为δ=1.0。为此,采用EWMA控制图对轴的直径进行过程监控,下面研究监控轴直径的EWMA控制图参数选取具体步骤:
1)在一定置信度(α=0.005)下,确定受控平均运行链长ARL0(200)、马尔可夫链的子区间划分数k(50)以及欲控偏移量δ(本例中为1.0);
2)设δ=0,采用java计算程序,根据已知条件,计算出在不同λ下满足ARL0的L,通常选取λ=0.1,0.2,L,0.9,见表1。然后采用回归方法求出L与λ之间的关系式,如式15所示。

表1 几组符合条件的(λ,L)值对计算结果

采用基于J2EE开发的控制图参数优化系统演示λ与L的拟合曲线,得到λ与L之间的拟合曲线如图6所示。

图6 λ与L拟合曲线图
3)在λ轴以0.01为间距,在λ、L的关系曲线上获得(λ,L)值对。
4)计算取不同(λ,L)值对、过程偏移量δ=1.0时的ARL0值。的计算结果曲线如图7所示。

图7 δ=1.0时ARL1.0与λ的关系曲线
5)从ARL1.0与λ的关系曲线,计算得到ARL1.0的最小值min(ARL1.0)=8.1341,以及此时对应的平滑系数λ0=0.17,在图6上计算λ0=0.17所对应的控制线L0=0.17。此时的λ0=0.17、L0=2.6517即为该条件下EWMA控制图的优化参数。对于优化后的EWMA控制图,其在不同偏移量下的OC曲线如图8所示。
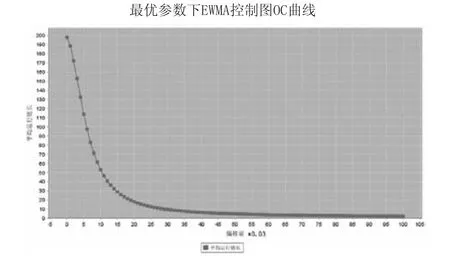
图8 δ=1.0时最优参数下的OC曲线
在相同置信度α=0.9973及偏移量δ=0.17下,用matlab仿真休哈特控制图和取不同参数的EWMA控制图的ARL随均值漂移的变化情况,表2比较了ARL计算结果:
由上述分析可见,当均值发生微小偏移δ>0.5σ时,EWMA控制图能比休哈特控制图更即时地检测出异常,因此对小偏移的控制更为灵敏,且在相同置信度α=0.9973下,参数取λ0=0.17、L0=2.8912时对偏移量δ=1.0最敏感,参数(λ0=0.17、L0=2.8912)即为置信度α=0.9973、偏移量δ=1.0下设计出的最优参数组合。
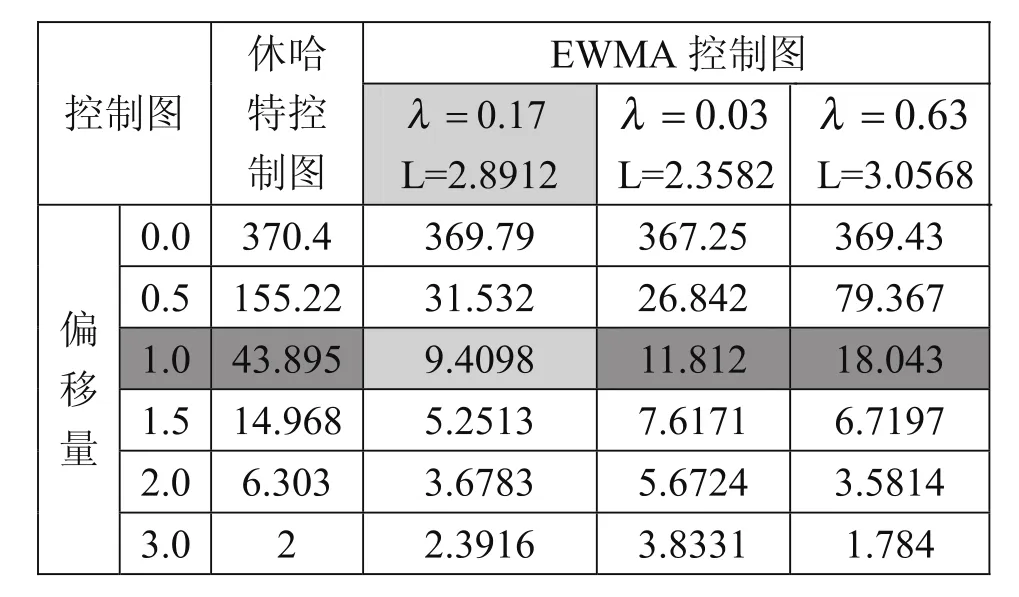
表2 休哈特控制图与EWMA控制图不同参数下的ARL
6 结论
本文研究监控小偏移过程的EWMA控制图参数(λ、L)优化问题,基于马尔可夫链法对EWMA控制图的参数优化算法进行深入研究,并用matlab对EWMA控制图参数优化算法进行仿真验证,总结出在一定置信度及特定小偏移量下计算最优参数组合的一般步骤,通过比较验证了优化参数的正确性,在上述研究的基础上,基于J2EE平台实现了控制图参数优化系统界面。
[1]杜福洲.多元统计过程控制与诊断方法研究[D].北京:北京航空航天大学,2006,9.
[2]杜福洲,唐晓青,孙静.MEWMA控制图运行链长分析及实例研究[J].中国机械工程,2007,18(7):820-824.
[3]杜福洲,孙静,唐晓青.基于马尔可夫链的MCUSUM控制图运行链长分析[J].清华大学学报,2007,47(2)169-172.
[4]Dogan A.Serel, Herbert Moskowitz Joint economic design of EWMA control charts for mean and variance,2008,157-168.
[5]何曙光,何桢,齐二石.基于马尔可夫链模型的EWMA控制图性能分析与优化[J].系统工程与电子术,2008,6(30):1127-1130.
[6]Su-Fen Yang,Yi-Ning Yu A Using VSI EWMA charts to monitor dependent process steps with incorrect adjustment 2009 442-454.
Parameter optimization and implementation for ewma control chart based on markov chain
BAI Shuang-mei, DU Fu-zhou
EWMA控制图的性能取决于其参数的选取,学术界和工业界常采用平均运行链长作为控制图性能评价指标,本文对基于马尔可夫链的EWMA控制图的参数(平滑系数 、控制线参数 )优化问题进行了深入的研究:给出了一种EWMA控制图参数优化方法及一般步骤;采用matlab平台对该算法进行研究并基于J2EE平台实现EWMA控制图参数优化系统界面,给出示例计算,并与传统的控制图进行了比较研究。
EWMA控制图;小偏移过程;质量控制;matlab仿真;参数优化;系统实现
白双梅 (1985- ),女,内蒙人,硕士研究生,主要从事计算机集成制造、计算机辅助质量管理、过程管理等方面的研究。
TH166;021;0242;TP391
A
1009-0134(2010)06-0064-05
10.3969/j.issn.1009-0134.2010.06.22
2009-08-18
总装预研项目;国防基础科研项目
