内积空间上的矩阵pade型逼近的研究
2010-05-10万诗敏于鲁源
万诗敏,陈 娟,于鲁源
(1. 天津城市建设学院 基础学科部,天津 300384;2. 南通大学 理学院,江苏 南通 226007;3. 天津大学 理学院,天津 300072)
内积空间上的矩阵pade型逼近的研究
万诗敏1,陈 娟2,于鲁源3
(1. 天津城市建设学院 基础学科部,天津 300384;2. 南通大学 理学院,江苏 南通 226007;3. 天津大学 理学院,天津 300072)
通过构造一个内积空间的线性泛函,定义了一个新的矩阵 pade型逼近(MPTA).从而利用MPTA生成的一般函数形式和行列式形式,解决了分母可以是奇次的矩阵 pade型逼近问题,并举出实例.
矩阵的内积;矩阵型pade逼近;行列式
矩阵pade型逼近(matrix pade-type approximant,简称 MPTA)有各种各样的定义,笔者关注由 Graves-Morris和其他研究者在纯量方面的研究[1-3].Graves-Morris和 Robert[4]利用向量和矩阵同构,把向量型pade逼近扩展到矩阵 pade型逼近,并用 Clifford代数表示[4-6].一般矩阵型pade逼近的方法是在矩阵内积的基础上,定义一个一般的广义逆矩阵 pade型逼近(generalized inverse matrix pade approximation,简称 GIMPA).与现有的矩阵 pade型逼近相比[7],GIMPA无需构造矩阵的乘法,而是利用矩阵乘法的不可变换,通过控制阶数和分解来建立的.这一方法隐含了当n是奇数时,矩阵 pade型逼近[m n]不能建立的问题.
本文的目标是填补上述缺陷.在内积空间里,引入一般线性泛函,定义出一个新的矩阵 pade型逼近(MPTA),不同于向量型的 Clifford代数方法,也不同于矩阵型的 GIMPA方法,这是因为在它的计算中没有利用矩阵的广义逆,而是利用了幂级数的展开进行的.MPTA方法具有如下形式:①它的生成函数形式是来源于定义的;②其行列式形式与正交多项式相关.利用新的 MPTA,解决了n是奇数时的矩阵 pade型逼近,并举出实例进行说明.
1 矩阵型pade型逼近
设A=(aij),B= ( bij)∈ Cs×t,定 义 内 积(A, B)=

这里A *表示A的复共轭阵,引用相同的记号[4].基于式(1)和式(2),矩阵A的逆可相应定义为
设A , B∈ Cs×t,同样,如果内积(A, B ) =0,就称A正交于B.
设f( z)为一级数,其系数是s× t阶矩阵,即

设P是一元实变量的数量多项式集合,它的系数属于复数域C,且 Pk是P的元素中次数小于或等于k所构成的集合.
设φ:P→ Cs×t为P上一广义线性泛函,作用于x,定义为

对所给的级数(3),则由式(4)得

设v是nP中次数为n的一个数量多项式
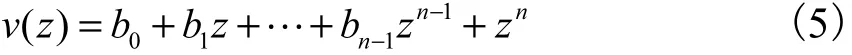
定义矩阵多项式w为
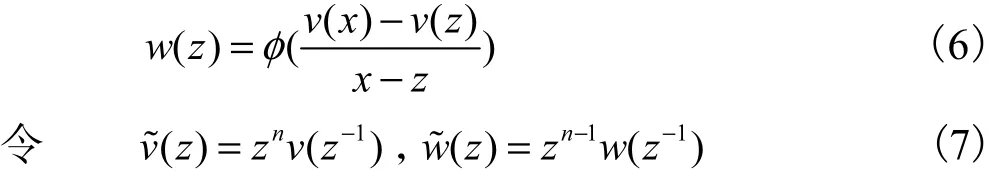
定理1- f( z) = O( z n),具体证明见文献[8].
定义1对于所给级数(3),一个矩阵pade型逼近定义为

设φ(l):P→ Cs×t为P上一个广义线性泛函,作用于x,定义为

基于式(10)和式(8),构造

定理2,具体证明见文献[8].
定义2)被称作是一个MPTA,定义为(mn)f(z).
例 1: 设

解:(i)这里,由式(8)和式(10)得到
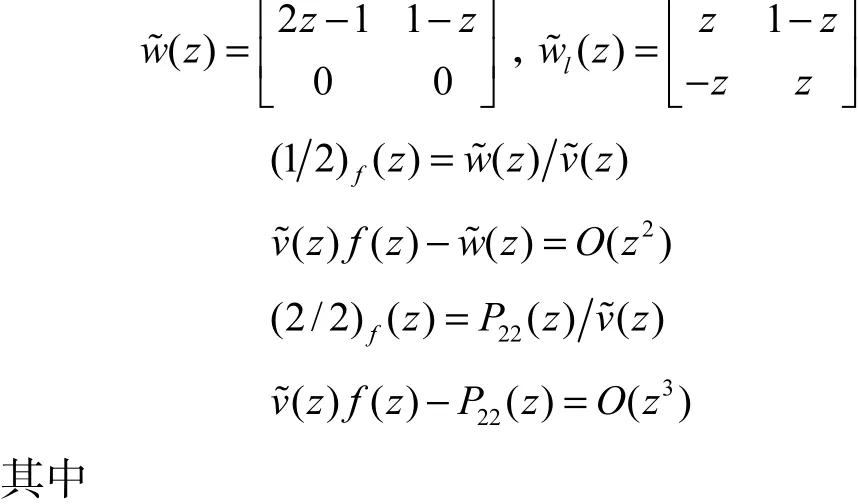

(b)ε-算法方法:通过利用广义逆矩阵(3),矩阵值的ε-算法定义为

(c)Thiele-型连分式方法:通过广义逆矩阵
(3)n步收敛的Thiele-型矩阵值连分式可构造为

上述方法表明:当n为奇数时,GIMPA 方法不能构建型为[m n]的pade逼近.




例2:设 f ( z)由例 1给定.寻找当 v( z)= (z - 1 )2·(z - 2 )时的.
解:由式(11)、式(7)和式(8)可以得到

[1]BAKER G A J, GRAVES-MORRIS P R. Padé approximants[M]. 2nd ed. New York:Cambridge University Press,1995.
[2]SAFF E B,VARGA R H.Pade and Rational Approximation[M]. New York:Academic Press,1977.
[3]GRAVES-MORRIS P R. Vector valued rational Ⅱ[J].IMA J Numer Anal,1984,4(4):209-224.
[4]GU C Q. Generalized inverse matrix valued padé approximation on the basis of scalar product[J]. Linear Algebra Appl,2001,322:141-167.
[5]GU C Q. Generalized inverse matrix valued padé approximants[J]. Numer Sinica,1997,19:19-28.
[6]陈 娟,顾传青. 基于广义逆矩阵 Thiele-型有理插值与ε-型有理插值[D]. 上海:上海大学,2008.
[7]徐献瑜,李家楷,徐国良.Padé 逼近理论[M]. 上海:上海科技出版社,1990.
[8]陈 娟,万诗敏. 内积空间上的矩阵型 pade逼近的代数性质[J]. 南通大学学报,2009,8(3):86-89.
Study on Matrix Pade-type Approximant in the Inner Product Space
WAN Shi-min1,CHEN Juan2,YU Lu-yuan3
(1. Department of Fundamental Subject,TIUC,Tianjin 300384,China;2. School of Science, Nantong University,Nantong 226007,China;3. School of Science,Tianjin University,Tianjin 300072,China)
A new Matrix Pade-type approximant (MPTA) is defined in the paper by constructing a generalized linear function in the inner product space. The general functional form and determinant form are generated by using MPTA,which solves the pade approximation problem for the matrix with denominator being odd matrix, and then some examples are enumerated.
inner product;MPTA;determinant
O151.21
A
1006-6853(2010)02-0141-04
2010-01-05;
2010-03-12
天津城市建设学院教育教学改革与研究项目(JG-0731)
万诗敏(1977—),男,安徽潜山人,天津城市建设学院讲师,硕士.
