从一道高考题的改编看物理模型的迁移

崔彩佳

(河北师大附中,河北 石家庄 050000)

笔者将2003年上海卷一题进行了改编,引导学生灵活创新,看到模型之间的联系与区别,将物理模型进行迁移,效果非常显著.

1 从原题看常规模型解法

图1

题目.(2003年上海物理卷)一质量不计的直角型支架两端分别连接质量为m和2m的小球A和B,支架的两直角边长度分别为2L和L,支架可绕固定轴在竖直平面内无摩擦转动,如图1所示.开始时OA边处于水平位置,由静止释放,则

(A)A球的最大速度为

(B)A球速度最大时,两个小球的总重力势能最小.

(C)A球速度最大时,两直角边与竖直方向夹角为45°.

(D)AB两球的最大速度之比为vA∶vB=2∶1.

答案:(B)、(C)、(D).

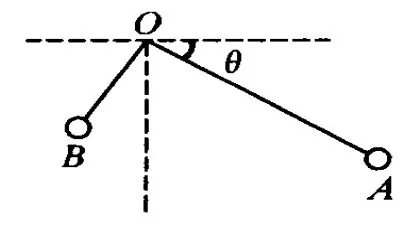
图2

此模型属于系统机械能守恒的模型,A、B组成的系统在运动过程中机械能守恒,当AB系统的重力势能减少最多时,系统动能最大,A、B速度最大,其中对于(C)选项的解答如下.

如图2所示,设OA杆转过的角度为θ,由机械能守恒定律得

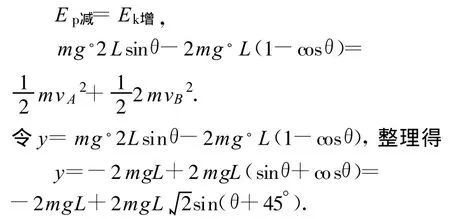
2 从改编后的两种解法看物理模型的迁移

改编原题,将原题中A、B两球的质量改成相同求解.

解法1:常规模型法

如图2,A、B组成的系统在运动过程中机械能守恒,当AB系统的重力势能减少最多时,系统动能最大,A、B速度最大.

由机械能守恒定律得

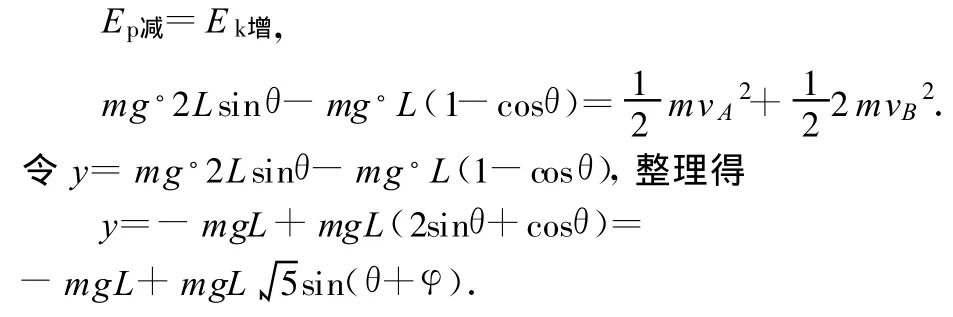
解法2:模型的迁移——单摆模型

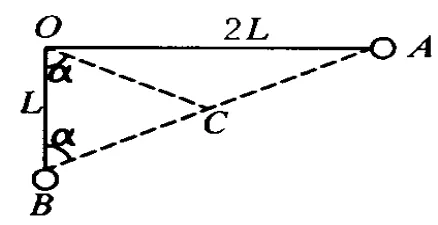
图3

因A、B两球质量相等,故我们可以找到两球的等效重心在两球连线的中点位置C,如图3,这样AB两球的运动就可等效为质点C的单摆运动,由单摆运动知识知,当点C运动到竖直最低点时速度最大,设OC转过的角度为α,由三角形知识,△OBC为等腰三角形得OC转过角度α=arctan2时速度最大,此即OA杆转过的角度,此结果α=arctan2与上述方法中的结果一致!

需要说明的是,如果两球质量不相等,等效重心不易找,此方法不提倡.

此方法一摆出,学生马上表现出了很高的积极性,课堂气氛马上活跃起来,如果我们在平时多进行这样的总结归纳,会达到事半功倍的效果.