用于整体光照的最小方差抽样

耿中元，徐 庆，孙济洲

(天津大学计算机科学与技术学院，天津 300072)

蒙特卡罗方法在整体光照和真实感图像合成领域占有重要地位，然而当抽样数目不足时这些方法合成的图像往往带有噪声．为了将噪声降低到可接受的程度，需要大量的抽样，花费很长的时间．图像平面自适应抽样是一种有效地减少噪声的方法，这种抽样方法在学术界备受关注．Dippe和Wold[1]使用随机抽样的方法来实现合成图像的反走样．Lee、Redner和Uselton[2]以抽样方差为标准，自适应地对像素做抽样．Purgathofer[3]和 Painter、Sloan[4]使用置信区间来指导自适应抽样．Tamstorf和 Jensen[5]对置信区间方法做了扩展，把颜色调和操作加入其中．Mitchell[6]和后来的 Simmons、Sequin[7]使用颜色对比作为自适应抽样的标准．Kirk和 Arvo[8]研究了自适应抽样算法中的统计偏差，并且提出了纠正偏差的方法．Bolin、Meyer[9]和 Ramasubramanian、Pattanaik、Greenberg[10]以及后来的 Farrugia、Peroche[11]提出了基于人眼视觉模型的自适应抽样方法．Rigau、Feixas和 Sbert[12-13]提出了基于信息熵的自适应抽样方法．Fan[14]将总体蒙特卡罗(population Monte Carlo，PMC)引入图形学，并且在 PMC的框架下提出了图像平面自适应抽样算法．

虽然自适应抽样的标准不同，但是现有的算法都是把直接光照和间接光照合在一起做抽样．一般情况下，直接光照和间接光照抽样的方差和耗时是不同的，因此，合在一起做抽样并不是最优的选择．笔者提出的自适应抽样方法将直接光照和间接光照分开，除了方差还考虑了时间因素的影响．通过推导，找到了新的抽样分配标准，使得在给定的时间里方差接近最小值．将此方法与 Mitchell[6]和 Fan[14]的方法进行了对比，结果表明，此方法明显提高了抽样的效率．文中分析了图像平面抽样的方差和方差最小化的方法，给出了算法实现，用两组场景测试了该算法并与其他算法进行了比较．

1 图像平面自适应抽样

1.1 抽样方差

整体光照可以分解为直接光照和间接光照两部分，像素值为

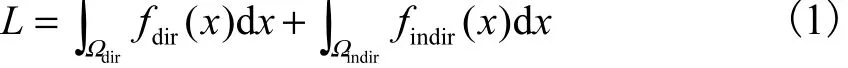
式中：L为像素值；fdir(x) 和 findir( x) 分别为用于计算直接光照和间接光照的被积函数；Ωdir和Ωindir分别为直接光照和间接光照的积分域．

使用蒙特卡罗随机抽样的方法求解式(1)，可得

直接光照和间接光照的积分可以分别抽样，也可以合并在一起抽样．假设仅用于直接光照的抽样数目为 n1，仅用于间接光照的抽样数目为 n2，直接光照和间接光照合并在一起的抽样数目为 n3，则直接光照的抽样数目 Ndir= n1+ n3，间接光照的抽样数目Nindir=n2+n3，进一步可以得到的方差为

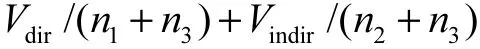
假设仅用于直接光照的抽样每个耗时1t，这类抽样总共耗时1T；仅用于间接光照的抽样每个耗时2t，这类抽样总共耗时2T；直接光照和间接光照合并在一起的抽样每个耗时3t，这类抽样总共耗时3T，则ˆL的方差可以表示为

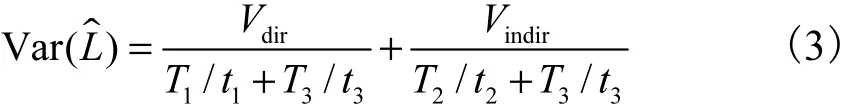
式(3)表示的是一个像素的方差．一幅图像由多个像素组成，所有像素的估计值的方差之和为

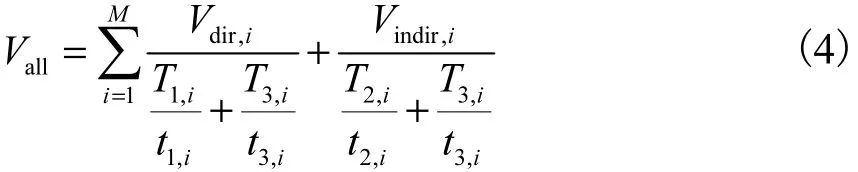
式中M为一幅图像包含的像素的数目．

1.2 方差最小化

在以下两种情况下，Vall的表达式可以退化为比较简单的形式．

情况 1对所有像素而言，把直接光照和间接光照合并在一起抽样．这时，Vall可以表示为

在这种情况下，当3,iT 满足

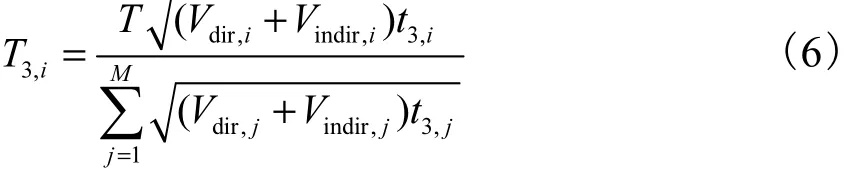
时，Vall取得最小值，此时像素i的抽样数目为 T3,i/ t3,i．

情况 2对所有像素而言，直接光照和间接光照分别抽样．这时，Vall可以表示为

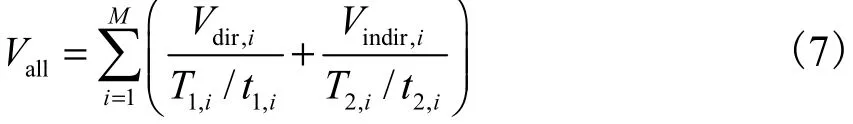
在这种情况下，当1,iT 和2,iT 满足式(8)的条件时，allV取得最小值，此时对像素i而言，直接光照抽样的数

目为 T1,i/ t1,i，间接光照抽样的数目为 T2,i/ t2,i．为了进一步节省时间，直接光照和间接光照公有的那部分抽样可以合并在一起．

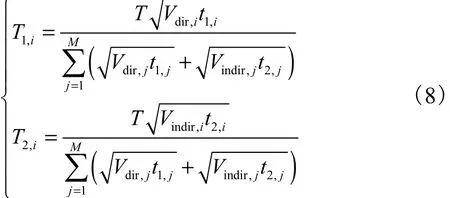
每一种情况的效率定义为

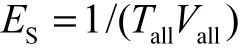
式中 Tall为整幅图像的耗时．分别计算以上两种情况的效率，然后选择效率较高的一种情况作为抽样数目的分配标准．

2 算法实现与结果讨论

蒙特卡罗抽样通常会有很大的方差，为了降低噪声，一个像素要用很多个抽样来计算，因此图像的绘制是一个迭代的过程．

笔者在基于物理的渲染工具包(physically based rendering toolkit，PBRT)引擎中实现了最小方差抽样算法．PBRT是一个开源的渲染引擎，研究人员可以在该引擎中实现不同的算法以比较它们的效率．图 1是图像平面自适应抽样算法的流程图．首先是 PBRT渲染引擎初始化，读入场景文件，读取纹理和多边形网格等场景数据，建立用于光线与场景求交点的 kd树．然后自适应抽样开始执行，测量抽样的耗时1t、2t和3t．事实上，一个抽样的耗时在几十微秒左右，测量某个像素内一个抽样的准确耗时是不可能的，如果使用大量的抽样测量时间，则用于自适应抽样的时间就相应地减少了，抽样的整体效率将受到影响．为了解决这个矛盾，笔者将整幅图像分块，每块含有10 10×个像素．算法测量每一块的抽样耗时，每块使用 32个抽样来测量，然后把耗时映射到每个像素．之后算法判断这一次是否为第 1次迭代抽样，如果是第 1次，则还没有数据来计算每个像素每种抽样的方差，这时在图像平面内均匀分配抽样的数目，如果不是第1次，在图像平面内自适应地分配抽样的数目；然后做抽样，用路径跟踪的方法计算光照，这次迭代抽样全部完成之后，计算每个像素每种抽样的方差以及图像的方差．如果图像的方差足够小则渲染过程结束，否则根据已有的所有抽样数据累计的结果来计算每个像素每种抽样的数目，然后进入下一次迭代．

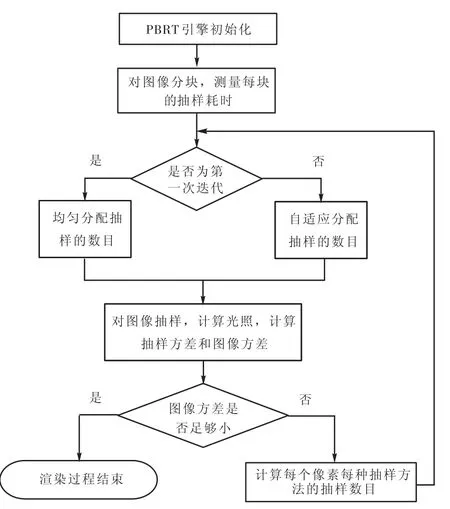
图1 图像平面自适应抽样算法流程Fig.1 Flow chart of image plane adaptive sampling algorithm

对于每一个像素，使用绘制过程中记录的抽样来计算dirV 和indirV ．令

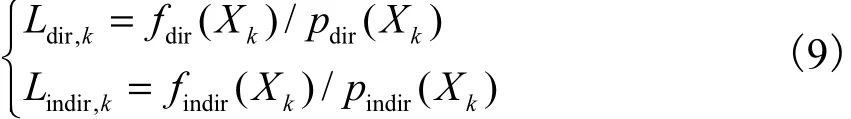
则 Vdir和 Vindir的估计式为

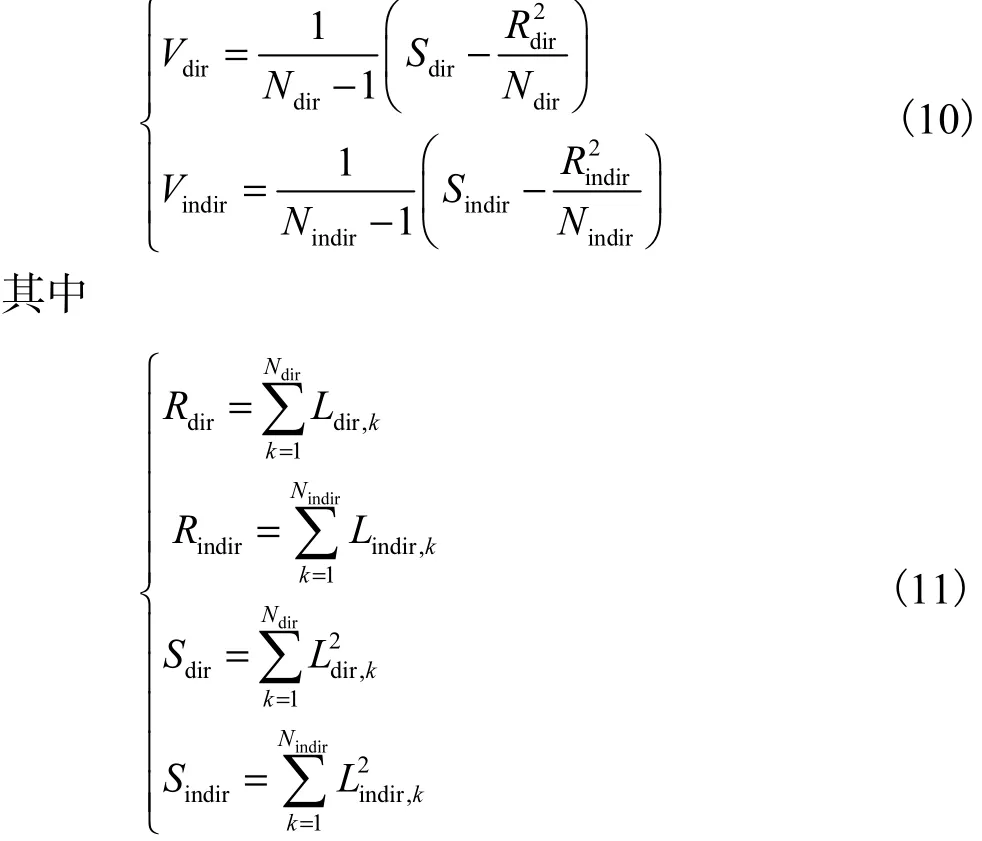
随着抽样数目的增加，Vdir和 Vindir逐渐收敛．由于抽样的随机性，某些像素的抽样方差的估计值可能为零．为了不漏掉任何一个像素，在自适应抽样的过程中，算法限制每个像素至少有一个直接光照和一个间接光照抽样．

笔者使用了两组场景来比较抽样的效率，在每一组场景中本文的算法分别与 Mitchell[6]和 Fan[14]的算法进行对比．为了表达简洁，本文的最小方差抽样方法(minimum variance sampling)缩写为 MVS，Mitchell[6]的基于颜色对比的自适应抽样方法(contrast based adaptive sampling)缩写为 CBAS，Fan[14]的总体蒙特卡罗框架下的图像平面自适应抽样方法(population Monte Carlo for image plane sampling)缩写为PMC-IP．

笔者使用了 3种标准来比较不同抽样方法的效率：一是均方差(mean square error，MSE)；二是均方根(root mean square，RMS)；三是 Lai等[15]中的标准，即

式中：e为作比较的图像与参考图像之间的差异；T为算法的耗时；E为抽样的效率．

Sponza Atrium场景的绘制图像的解析度为600×600，Villa场景的绘制图像的解析度为 1,000×600．Sponza Atrium场景的绘制结果如图 2所示，场景中一共有 169,200个三角面片，在距离地面很高的地方有一个大的面光源．Villa场景的绘制结果如图3所示，场景中一共有 463,700个三角面片，使用环境映射(environment mapping)作为光源．场景中的材质包含漫反射、镜面反射以及光泽反射属性，其中，光泽反射属性是基于Blinn微面片分布实现的．

为了辅助视觉上的比较，笔者在文中提供了参考图像．参考图像是使用蒙特卡罗路径跟踪算法[16]绘制的，每个像素使用了 32,768个抽样．为了便于比较，每幅图像的下面放置了图像的局部缩放．不同方法在不同场景中的定量比较结果详见表 1．除参考图像以外，每个场景的不同图像是使用相似的时间绘制的，具体耗时如表1所示．

从缩放图可以看到，与现有方法相比，新方法MVS的绘制效果更好，CBAS方法绘制的图像有更多的亮斑，而 PMC-IP方法绘制的图像有更多的暗斑，这一点在 Villa场景的玻璃柜上尤为明显(见图 3中的缩放图)．在表 1中的定量比较中，新方法的优势也是显而易见的，在耗时相近的前提下，新方法的均方差 MSE和均方根 RMS都比现有方法小．新方法的抽样效率比现有方法高，在 Sponza Atrium场景中，CBAS和PMC-IP的抽样效率分别是新方法MVS的87.1%和75.0%，在Villa场景中，CBAS和 PMC-IP的抽样效率分别是新方法MVS的42.5%和85.6%．对于给定的场景而言，本文的算法和已有算法的时间复杂度都是正比于图像像素的数目，本文的算法在自适应分配抽样时考虑了抽样的耗时和方差，并且用拉格朗日乘子法使给定时间内的方差接近最小值，所以本文的算法抽样效率更高．

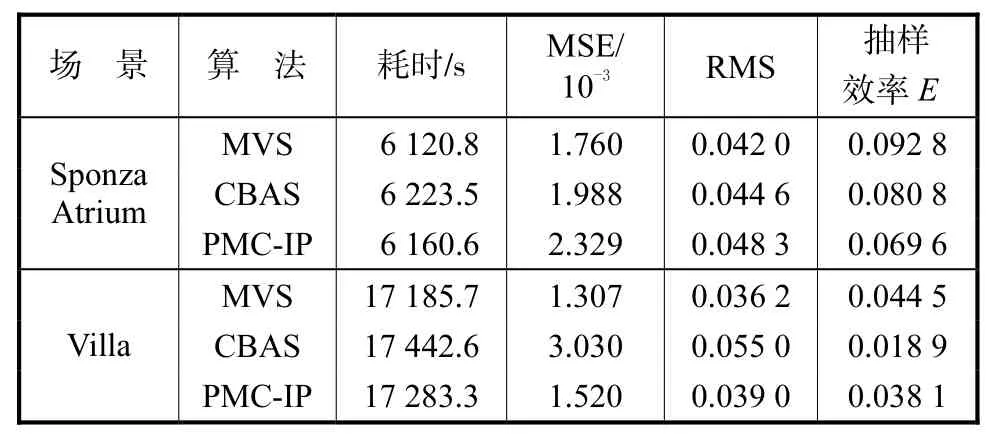
表1 不同算法的结果比较Tab.1 Comparison of results of different algorithms

图2 Sponza Atrium场景的绘制结果Fig.2 Rendering results of Sponza Atrium scene

图3 Villa场景的绘制结果Fig.3 Rendering results of Villa scene

3 结 论

(1)本文以给定时间内图像方差最小为目标，提出了新的图像平面自适应抽样方法．

(2)与现有方法相比，新方法的抽样效率更高，图像的方差更小．

(3)整体光照的抽样效率不仅与图像平面的抽样分布有关，与绘制点处的半球面抽样分布也有关．

今后的研究工作可以把最小方差抽样的思想应用于半球面抽样中，进一步提高整体光照的抽样效率．

［1］Dippe M A Z，Wold E H. Antialiasing through stochastic sampling[J].Computer Graphics，1985，19(3)：69-78.

［2］Lee M E，Redner R A，Uselton S P. Statistically optimized sampling for distributed ray tracing [J].ComputerGraphics，1985，19(3)：61-67.

［3］Purgathofer W. A statistical method for adaptive stochastic sampling[C]//Proceedings of the European Computer Graphics Conference and Exhibition：The Computer Interface.Amsterdam，Netherlands：North-Holland，1986：145-152.

［4］Painter J，Sloan K. Antialiased ray tracing by adaptive progressive refinement[C]//Proceedings of the 16th Annual Conference on Computer Graphics and InteractiveTechniques.New York：ACM，1989：281-288.

［5］Tamstorf R，Jensen H W. Adaptive sampling and bias estimation in path tracing[C]//Proceedings of the Eighth Eurographics Workshop on Rendering.New York：Springer Wien，1997：285-296.

［6］Mitchell D P. Generating antialiased images at low sampling densities[C]//Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques. New York：ACM，1987：65-72.

［7］Simmons M，Sequin C H. Tapestry：A dynamic meshbased display representation for interactive rendering[C]//Proceedings of the Eurographics Workshop on Rendering Techniques.London：Springer-Verlag，2000：329-340.

［8］Kirk D，Arvo J. Unbiased sampling techniques for image synthesis[J].Computer Graphics，1991，25(4)：153-156.

［9］Bolin M R，Meyer G W. A perceptually based adaptive sampling algorithm[C]//Proceedings of the 25th Annual Conference on Computer Graphics and Interactive Techniques.New York：ACM，1998：299-309.

［10］Ramasubramanian M，Pattanaik S N，Greenberg D P. A perceptually based physical error metric for realistic image synthesis[C] //Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques.New York：ACM Press/Addison-Wesley Publishing Company，1999：73-82.

［11］Farrugia J P，Peroche B. A progressive rendering algorithm using an adaptive perceptually based image metric[J].Computer Graphics Forum，2004，23(3)：605-614.

［12］Rigau J，Feixas M，Sbert M. New contrast measures for pixel super sampling[C]//Proceedings of CGI’02.Germany：Springer-Verlag，2002：439-451.

［13］Rigau J，Feixas M，Sbert M. Entropy-based adaptive sampling[C]//Graphics Interface2003. Halifax，Canada，2003：149-158.

［14］Fan S. Sequential Monte Carlo Methods for Physically Based Rendering[D]. Madison，USA：University of Wisconsin-Madison，2006.

［15］Lai Y C，Fan S，Chenney S，et al. Photorealistic image rendering with population Monte Carlo energy redistribution[C]//Eurographics Symposium on Rendering2007.Grenoble，France，2007：287-296.

［16］Kajiya J T. The rendering equation[J].Computer Graphics，1986，20(4)：143-150.