基于Hough变换的椭圆检测算法

袁 理，叶 露，贾建禄，2

（1.中国科学院长春光学精密机械与物理研究所，吉林长春130033；

2.中国科学院研究生院，北京100039）

基于Hough变换的椭圆检测算法

袁 理1，叶 露1，贾建禄1，2

（1.中国科学院长春光学精密机械与物理研究所，吉林长春130033；

2.中国科学院研究生院，北京100039）

为了实现光电仪器对椭圆形目标的准确识别与跟踪，基于Hough变换提出了一种新的椭圆检测算法。该算法随机采样2点，再利用椭圆极和极弦的性质来搜索第3点并筛除大量无效采样；然后，以这3点为中心作正方形窗口，用窗口内的所有点来拟合椭圆方程。在验证候选椭圆时，提出了一种新方法来判断边缘点是否在椭圆上，并且给出了确定真实椭圆的自适应阈值。实验显示，该算法的平均长度误差为0.5 pixel，平均角度误差为0.6°，平均耗时为79 ms，表明该算法精度高，速度快，检测性能较好。

椭圆检测；随机采样；无效采样；椭圆拟合

1 引 言

为了实现光电仪器对椭圆形目标的识别与跟踪，需要从光电仪器所采集的图像中检测出椭圆。Hough变换［1］是形状检测的一种基本方法，但是椭圆的参数较多，如果用Hough变换来检测椭圆，消耗的时间和内存是难以接受的。Xu［2］等人提出了随机Hough变换（Random Hough Transfor，RHT），主要通过随机采样与动态链表存储来降低计算时间与内存需求。但是，RHT无目标的采样会引入大量的无效累积，浪费大量的计算时间和存储空间。为此，一些文献对RHT算法做了改进来检测椭圆。文献［3］先搜索图像中的连续曲线，然后在同一连续曲线上采样5点来计算椭圆参数，这样提高了5点在同一个椭圆上的概率，但是搜索连续曲线太费时，而且对于边缘不连续的椭圆，检测效果不好。文献［4］随机采样6个点，若6个点都在一个椭圆上，则该椭圆成为可能椭圆，但随机采样的6个点都在一个椭圆上的概率太小，因此无效采样也很多。文献［5］利用3个点和其中2个点的切线方向来求椭圆方程；文献［6］利用2点及其切线方向来提取椭圆中心，但是由于切线方向的误差较大，所以这两种方法的精度都不高。为了进一步减少椭圆检测的时间，提高检测准确性，本文在RHT的基础上设计了一种新的椭圆检测算法。

2 椭圆检测算法

2.1 随机采样2点

对采集到的图像进行去噪、边缘提取和二值化后，得到目标的边缘图像。在所有边缘点中，本文只随机采样2点。与随机采样5点或者3点相比，只随机采样2点大大增加了采样点全部落在同一个椭圆上的概率，减少了无效采样。为了减小误差，采样的2点之间的距离不能太小，因此设置一个适当的阈值d，如果2点的距离＜d，则放弃该2点，重新采样。

2.2 椭圆极和极弦性质的利用

随机采样得到2点后，可利用椭圆极和极弦的性质来搜索第3点并筛除无效采样。椭圆的极和极弦性质如下［7］：如图1所示，P1，P2为椭圆上两个点，P1T和P2T为椭圆的两条切线，两切线交于T，T称为椭圆的极，弦P1P2称为椭圆的极弦。设P1P2的中点为M，TM的中点为G，则有以下两结论成立：1）线段TM与椭圆的交点P3必在线段GM上；2）P3处的切线l1和弦P1P2平行。

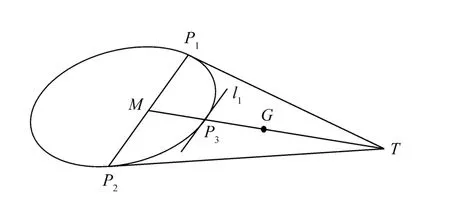
图1 椭圆的极和极弦的性质

设随机采样得到的2点为P1，P2，它们的梯度方向的斜率kt可用Sobel算子求出［8］，则切线方向的斜率kP＝-1/kt，然后，可以求出切线P1T和P2T的方程，进而求出T、M和G点的坐标。接着，在线段GM上搜索第3个椭圆点P3。假设边缘点为Q，如果Q不在线段GM上，则必有|GQ|+|QM|＞|GM|；如果Q在GM上，则必有|GQ|+|QM|＝|GM|。考虑图像的离散性，这里设置正阈值ε，若Q点满足|GQ|+|QM|＜|GM| +ε，则认为Q点在GM上，即在GM上搜索到了一个椭圆点Q。本文中ε取1。遍历所有边缘点后，如果GM上没有搜索到点，则说明P1，P2点不在同一个椭圆上，则放弃这2点；若搜索到了，说明P1、P2点可能在同一个椭圆上，则继续计算。

在GM上搜索到的点往往不止一个，可以从中随机取出一个，将它作为P3点。然后，检验P3处的切线l1与弦P1P2是否平行。考虑到切线方向的误差，如果l1与P1P2的夹角＜10°，即认为平行，则说明P1，P2，P3可能在同一个椭圆上，继续后续计算；如果不平行则放弃该3点并重新采样。在以上过程中，对切线方向误差的影响分析如下：第一，如果P3在椭圆上，切线误差会使l1与P1P2的夹角不为0，但绝大多数情况下仍＜10°，所以仍然判断l1与P1P2平行，不会将P3漏判；即使在极少数误差很大的情况下出现漏判，也仅仅是浪费一次有效采样而已，由于采样的次数很多，对整个椭圆检测的影响不大。第二，如果P3点不在椭圆上，在大多数情况下l1与P1P2的夹角远＞10°，即使有切线误差的影响也不会变化到10°以内，所以不会将P3误判为椭圆点；即使在极少数的情况下出现误判，由于后面还有投票的检验和边缘点数的检验，该虚假椭圆也会被排除。

本文充分利用了椭圆极和极弦的性质，不仅搜索到了第3个椭圆点，还筛除了大量不共椭圆的无效采样，减少了无效累积。

2.3 用最小二乘法拟合椭圆

现在已经得到了可能共椭圆的3点P1，P2，P3，但3点不足以确定椭圆方程。考虑到当一个点在椭圆上时，它附近的点在同一个椭圆上的概率很大。因此，分别以P1，P2，P3为中心作3个正方形的小窗口，对窗口内的所有边缘点作椭圆最小二乘拟合。在确保能够得到5个以上边缘点的情况下，窗口的边长要尽量小，以防止将椭圆以外的噪声点也包含进来，一般可取3。设椭圆方程为：

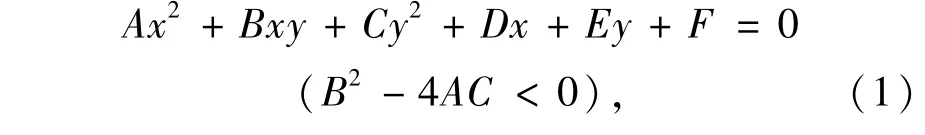
由于椭圆只有5个独立参数，所以可以把参数F定为一个固定的任意值，本文取F＝100。将窗口内的点代入式（1），得到一个超定线性方程组，设为UX＝V，求解其法方程UTUX＝UTV，即可得到椭圆的最小二乘解，如果该解满足椭圆判别式B2-4AC＜0，则把求出的椭圆参数加入动态链表进行投票累积。

本文没有像文献［5］那样用切线方向来直接求解椭圆参数，避免了切线方向误差对椭圆参数的影响，提高了椭圆的检测精度。

2.4 判断点是否在椭圆上的新方法

当投票累积值达到阈值时，该椭圆成为候选椭圆，接着就需要验证该椭圆上的边缘点的数目。由于图像的离散性，边缘点一般不会准确地满足式（1），因此需要找出判断边缘点是否在椭圆上的办法。很多文献［4］采用了如下传统方法：若边缘点满足

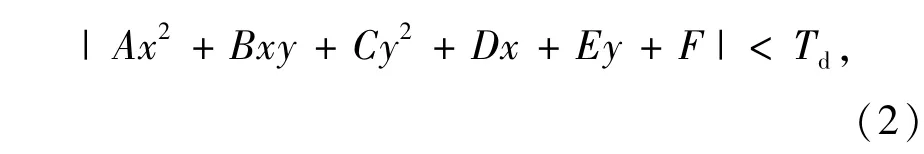
则认为该边缘点在椭圆上；但是阈值Td却难以确定，通过大量的实验发现，当Td取一个固定值时，对于不同的椭圆，其宽严程度有很大的不同。图2是当Td取0.5时由式（2）画出的不同椭圆的图像，可见，不同椭圆的边缘厚度相差很大，这种方法是不可取的。

图2 传统方法画出的椭圆图像

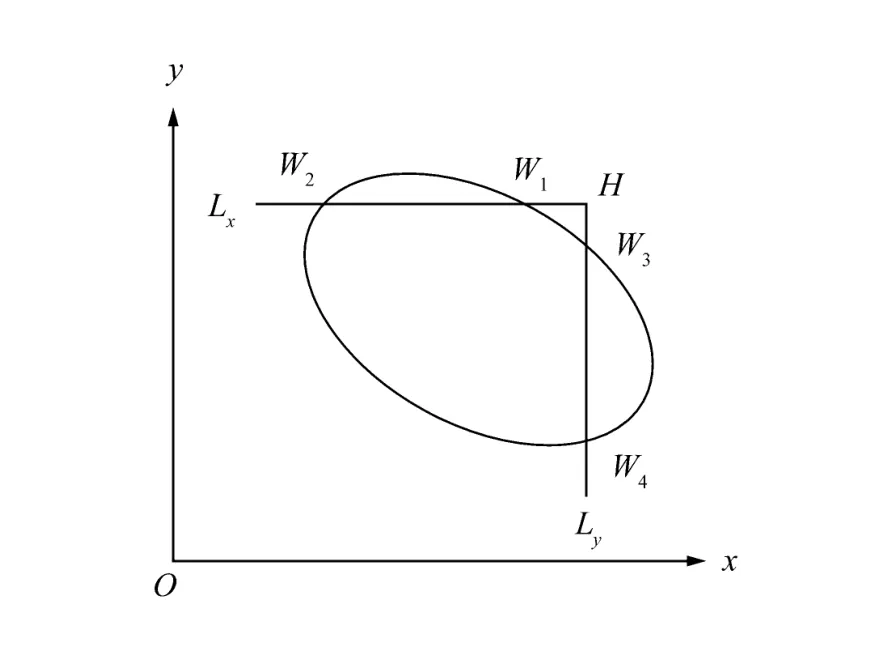
图3 判断边缘点在椭圆上的新方法

经过大量实验和研究，本文提出一种新方法来判断边缘点是否在椭圆上。如图3所示，设任一边缘点为H，过H点分别作平行于x轴和y轴的直线Lx和Ly，Lx和Ly与椭圆共有0到4个交点，如果这些交点中存在与H的距离＜η的交点，则判断H点在椭圆上；如果没有与H的距离＜η的交点，则判断H点不在椭圆上。其中η为阈值，本文取0.5。图4是当η取0.5时由新方法画出的不同椭圆的图像，其中所有椭圆的边缘都细而均匀，效果远远胜过图2。可见，新判断方法对不同椭圆的宽严程度是完全一样的。

图4 新方法画出的椭圆图像

2.5 椭圆上边缘点数阈值的确定

如果候选椭圆上的边缘点数超过阈值Mmin，即可以确定为真实椭圆。对于不同的椭圆，应该有不同的自适应阈值Mmin。设实际椭圆弧长度与理论的椭圆周长之比为λ，则真实椭圆的阈值

Mmin＝λ×π［1.5（a+b） -，（3）其中a、b是椭圆的两个半轴长，可由式（1）的系数来计算，π［1.5（a+b）-是椭圆周长的近似计算公式。

2.6 算法步骤

（1）计算图像中各点的梯度斜率kt并存储；

（2）对图像进行中值滤波去噪，然后用Canny算子提取边缘并二值化；

（3）构造边缘点集D，初始化参数单元集P＝NULL，循环次数k＝0；

（4）从D中随机选取2个点P1，P2，如果距离|P1P2|＞d，转（5）。否则转（11）；

（5）按图1所示在GM上搜索椭圆点P3，如果搜索到了，转（6）。否则转（11）；

（6）检验P3处的切线与弦P1P2是否平行，若是，转（7）。否则转（11）；

（7）以P1，P2，P3三点为中心作正方形窗口，将窗口内的所有点做最小二乘拟合，得到椭圆参数p，如果p满足判别式B2-4AC＜0，转（8）。否则转（11）；

（8）在P中找一个pc满足|p-pc|≤δ，δ是容许误差，若找到了则转（10）。否则，转（9）；

（9）将p插入P，令其value为1，转（11）；

（10）将pc的value加1，若小于阈值Nt（取2或3），转（11）。否则，转（12）；

（11）k＝k+1，若k＞Kmax，结束。否则，转（4）；

（12）pc为候选椭圆的参数，验证该参数对应椭圆上的点数M，若M＞Mmin，转（13）。否则，为虚假椭圆，从P中去除pc，转（4）；

（13）检测到参数为pc的真实椭圆，判断已检测到的椭圆是否达到规定的数目，若是，结束；否则，将落在参数pc对应椭圆上的点从D中去掉，重置P＝NULL，k＝0，转（4）。

3 实验结果

图5 实验用图

为了验证本算法的有效性，用VC编程进行实验。如图5是一幅400×300的图像，其中的两个碗呈现椭圆形。在配置为Intel酷睿双核E4600的CPU（2.4 GHz）和1 G内存的计算机上，用本文的算法和文献［4］、［5］的算法分别对图像中的两个椭圆检测了20次，并由式（1）的系数计算出了椭圆的几何参数。表1是检测的平均结果，其中椭圆参数的列出顺序为：中心坐标（pixel）；两半轴长（pixel）；对称轴倾角（°），耗时的单位为ms。进一步可算出本文算法的平均长度误差为0.5 pixel，平均角度误差为0.6°，平均耗时为79 ms；而文献［4］分别为1.2 pixel，0.9°，301 ms；文献［5］分别为2.0 pixel，1.1°，114 ms，可见本算法检测精度较高、速度较快。

表1 3种算法各检测20次的平均结果Tab.1 Average results of detecting ellipses for 20 times using threemethods

4 结 论

为了实现光电仪器对椭圆形目标的准确识别与跟踪，提出了一种新的椭圆检测算法。该算法有如下优点：（1）只随机采样2点，增加了采样点全部落在同一个椭圆上的概率，减少了无效采样；（2）利用椭圆极和极弦的性质搜索到了椭圆上的第3点，并筛除了大量无效采样，减少了无效累积；（3）用最小二乘法拟合椭圆方程，避免了用切线计算椭圆参数带来的误差；（4）提出一种新方法来判断边缘点是否在椭圆上，该方法对不同椭圆的宽严程度完全一样，大大优于传统方法。实验表明，该算法精度高、速度快，是一种较好的椭圆检测算法。

［1］HOUGH PV C.Methods and means for recognizing complex patterns：US，3069654［P］.1962-12-18.

［2］XU L，OJA E.A new curve detectionmethod：Randomized Hough Transform（RHT）［J］.Pattern Recognition Lett.，1990，11（5）：331-338.

［3］王成儒，胡正平，练秋生.一种高效的混合圆/椭圆检测方法［J］.贵州工业大学学报（自然科学版），2002，31（4）：100-103.

WANG CH R，HU ZH P，LIAN Q SH.A new efficienthybrid circle and ellipse fast detectionmethod［J］.J.Guizhou University Technol.（Natural Science Edition），2002，31（4）：100-103.（in Chinese）

［4］薛程，王士同.一种新的不基于Hough变换的随机椭圆检测算法［J］.微计算机信息，2006，22（1）：265-268.

XUE CH，WANG SH T.A new non-HT-based randomized algorithm for detecting ellipses［J］.Control＆Automation，2006，22（1）：265-268.（in Chinese）

［5］于莉娜，胡正平，练秋生.基于改进随机Hough变换的混合圆/椭圆快速检测方法［J］.电子测量与仪器学报，2004，18（2）：92-97.

YU LN，HU ZH P，LIAN Q SH.Hybrid circle and ellipse fast detection using improved randomized Hough transform［J］.J.Electronic Measurement and Instrument，2004，18（2）：92-97.（in Chinese）

［6］于海滨，刘济林.基于中心提取的RHT在椭圆检测中的应用［J］.计算机辅助设计与图形学学报，2007，19（9）：1107-1113.

YU H B，LIU JL.Ellipse detection by the RHT based on center extraction［J］.J.Computer-Aided Design＆Computer Graphics，2007，19（9）：1107-1113.（in Chinese）

［7］陈燕新，戚飞虎.一种新的基于随机Hough变换的椭圆检测方法［J］.红外与毫米波学报，2000，19（1）：43-47.

CHEN Y X，QIF H.A new ellipse detection method using randomized Hough transform［J］.J.Infrared Millim.Waves，2000，19（1）：43-47.（in Chinese）

［8］瞿钧，甘岚.梯度Hough变换在圆检测中的应用［J］.华东交通大学学报，2007，24（1）：101-104.QU J，GAN L.The application of grads Hough transformation in circle detection［J］.J.East China Jiaotong University，

2007，24（1）：101-104.（in Chinese）

Ellipse detection algorithm based on Hough transform

YUAN Li1，YE Lu1，JIA Jian-lu1，2
（1.Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033，China；
2.Graduate University of Chinese Academy of Sciences，Beijing 100039，China）

In order to ensure that photoelectric instruments can identify and track elliptical objects accurately，a new algorithm based on Hough transform is proposed.The new algorithm randomly samples two points，and then searches the third point using the characters of ellipse′s pole and pole chord，and eliminates lots of invalid samples.In the following，it uses the three points as the centers tomake three square windows，and then all the points in the windows are used to fit the ellipse.When a candidate ellipse is validated，a new method is proposed to judge if edge points are on the ellipse，and an adaptive threshold is supplied to confirm real ellipses.The experiment indicates that the algorithm′s average length error is 0.5 pixel，average angle error is 0.6°，and the average time needed is79 ms.In conclusion，the algorithm has high precision and high speed，and shows a good capability of detecting ellipses.

ellipse detecting；random ly sampling；invalid sample；ellipse fitting

2010-03-11；

2010-05-13

TP301.6

A

1674-2915（2010）04-0379-06

袁 理（1983—），男，四川泸州人，研究实习员，硕士，主要从事光学检测、图像识别等方面的研究。

E-mail：yuanlideyoux8852＠yahoo.cn