天目山常绿阔叶林空间点格局分形关联维数分析

陈永刚，汤孟平，胡 芸

（1. 浙江农林大学 环境科技学院，浙江 临安 311300；2. 浙江农林大学 信息工程学院，浙江 临安 311300）

天目山常绿阔叶林空间点格局分形关联维数分析

陈永刚1,2，汤孟平1，胡 芸2

（1. 浙江农林大学 环境科技学院，浙江 临安 311300；2. 浙江农林大学 信息工程学院，浙江 临安 311300）

摘要：利用分形中的关联维数D来进行天目山常绿阔叶林种群的空间点格局分析，首先，根据树木坐标建立树木两两之间距离矩阵Dn×n；其次，根据距离矩阵Dn×n计算不同距离步长△r下的距离标度r和r距离标度下树木的数目N(r)；最后，计算出关联维数D并根据D得出研究区域的空间分布格局。结果表明，天目山常绿阔叶林研究样区内的树木在空间分布格局上趋于集聚，其关联维数可以用来准确判定空间点格局分布。

关键词：点格局分析；分形；关联维数

种群的空间点格局分析是研究种群特征、种群间相互作用以及种群与环境关系的重要手段，在生态学中一直是研究的热点之一[1～5]。种群的空间点格局分析常用方法有Ripley’s K指数方法[6～7]、随机区块法[8]等方法。关联维数D能够判断物体的空间分布格局[9～10]。马克明、朱金兆等利用关联维数的方法计算种群的空间格局[11～12]。分形维数是从密度的多点相关出发，描述系统要素的相对分布状态[13]。利用D表征空间点格局分布的几何特征，计算过程简单直观。本文首先构建空间距离矩阵Dn×n，其次计算空间关联函数C(r)和不同距离标度r下的关联维数D，最后利用D来分析天目山常绿阔叶林种群的空间点格局分布。

1 研究区概况及数据来源

1.1 研究区域概况

天目山国家级自然保护区坐落于浙江省西北部（119° 23′ 47″～119° 28′ 27″ E，30° 18′ 30″～30° 24′ 55″N），距杭州约94 km。年降水量1 390～1 870 mm；年平均气温为14.8～8.8℃。受海洋暖湿气候影响，森林植被丰茂。植被分布呈垂直带状分布，自山麓到山顶垂直带谱为：海拔870 m以下为常绿阔叶林；870～1 100 m为常绿落叶阔叶混交林；1 100～1 380 m为落叶阔叶林；1 380～1 506 m为落叶矮林。常绿阔叶林是自然保护区内重点保护植被类型[4]。

1.2 数据来源

采用全站仪测量每株树木根部的坐标（x，y），其中：x，y是自定义的独立坐标系中的平面直角坐标。样地大小布设为100 m×100 m，采用相邻格子调查方法，把样地划分为100个10 m×10 m的调查单元。在每个调查单元内，对胸径≥5 cm的木本植物进行每木调查，记录树木种类，测定每株树木的胸径、树高等因子。对采集到的数据进行质量检验，删去记录信息不全的样本，树木总株树为1 802株。

2 研究方法

2.1 距离矩阵

空间距离矩阵是利用每株树木的（x，y）坐标，利用下式计算树木i与树木j之间的距离：

式中，（xi，yi）为树木i的平面坐标，（xj，yj）为树木j的平面坐标，dij为树木i与树木j之间的距离。

建立距离矩阵，矩阵中的元素dij为树木i与j之间的距离，对角线上的元素全部为0。距离矩阵Dn×n如下：

2.2 空间关联函数C(r)与Heaviside阶跃函数

Grassberger和Procaccia提出关联维数算法（G-P算法）[14～15]；刘继生等[13]、岳文泽[9]等利用G-P算法计算城镇体系的分形特征；徐建华等利用分形理论分析西北干旱区景观的镶嵌特点；其空间关联函数C(r)定义如下：

式中，N为距离矩阵Dn×n中的行数（列数）；r为指定距离标度；dij为树木i与j之间的距离；N(r)为距离标度r下，树木的株数；H为Heaviside阶跃函数；H(r-dij)定义如下：

2.3 标度r，空间关联函数C(r)与关联维数D

空间关联函数C(r)的取值与标度r有关，空间关联函数C(r)与标度r存在如下关系：

由式（5）可得式（6）：

为了计算方便，可以利用下式：

式中，N(r)为r距离标度下的距离数目。对(7)式两边取对数，可得：

式中，A为常数项。

关联维数反映了对象之间相互作用的规律性[10,13]，其值大小表征了该区域内对象之间空间分布的集中或分散程度。实际意义上，D值是介于1和2之间的，种群关联维数大（接近2），表明种群个体的空间相关程度较高，个体聚集，种群整体对空间的占据程度较高；反之，关联维数小（远离2），则种群个体空间相关程度低，个体聚集程度低，种群对空间的占据能力较低。D值小于1和大于2均没有意义。计算种群格局关联维数的过程中，如果只存在一个有意义的线性无标度区，表明种群个体空间分布都遵从相同的规律，即每一个体周围随距离标度r的增加，个体数的增长规律均相同，统计意义上种群个体分布是非聚集的。如果直线拟合过程中出现拐点，则表明种群个体空间相关程度在拐点尺度前后的两个尺度域内不同，反映出种群格局在不同尺度上存在着显著差异，它揭示种群个体的聚集规模[11～12,16]。

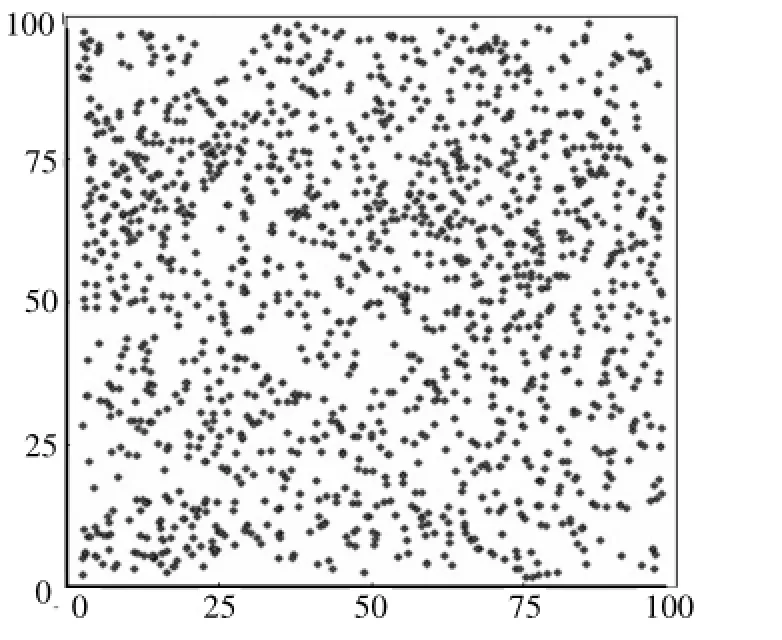
图1 树木调查点位图Figure 1 Map of investigated trees

3 结果与分析

3.1 树木间距离矩阵计算

将调查的数据按照固定的格式输入Excel文件，在ArcGIS 9.2中，根据Excel文件中的坐标（x，y）生成树木调查点位图.shp文件，结果如图1。

利用公式（1），通过GeoDa软件，计算树木两两之间的距离并生成空间距离矩阵，距离矩阵是一个对称矩阵，只写半角，结果如表1。

3.2 不同步长△r计算N(r)

根据表1中调查样地树木间的空间距离矩阵，以不同步长△r，计算N(r)。N(r)的最大值为，即1 802

株树木之间可有1 622 701组距离。因样地的大小为100 m×100 m，故两株树木的最大间距为141.42 m。步长△r分别取0.25、0.5、1.0、2.50、5.00、7.50、10.00 m。结果列于表2至表7中。

表1 调查样地树木间空间距离矩阵Table 1 Space distance matrix between investigated sample trees

表2 步长△r= 0.25 m下，距离标度r及距离标度下的树木数N(r)Table 2 Step length△r= 0.25 m, scale-free r and the number of treesN(r)

表3 步长△r= 0.5 m下，距离标度r及距离标度下的树木数N(r)Table 3 Step length△r= 0.5 m, scale-freerand the number of treesN(r)

表4 步长△r= 1.00 m下，距离标度r及距离标度下的树木数N(r) Table 4 Step length△r= 1.00 m, scale-freerand the number of treesN(r)

表5 步长△r= 2.50 m下，距离标度r及距离标度下的树木数N(r)Table 5 Step length△r= 2.50 m, scale-freerand the number of treesN(r)

表6 步长△r= 5.00 m下，距离标度r及距离标度下的树木数N(r)Table 6 Step length△r= 5.00 m, scale-freerand the number of treesN(r)

表7 步长△r= 10.00 m下，距离标度r及距离标度下的树木数N(r)Table 7 Step length△r =10.00 m, scale-free r and the number of trees N(r)

用不同的步长△r去度量在r距离标度下的树木数N(r)，相当于用最小分隔为△r的尺子去量测r尺度下的树木数N(r)。使用不同的步长△r相当于在不同的尺度下测定树木间的空间分布格局。当步长△r> 10.00 m时，也即相当于采用分隔大于10.00 m的尺子去度量大小为100 m×100 m的研究样区内的数据，由于分隔太大细节信息已经丢失。故不测定步长△r> 10.00 m时的距离标度r及其标度下的树木数N(r)。

3.3 关联维数计算

对表2至表7中的数据，分别按公式（8）进行计算并做回归图，结果如图2。

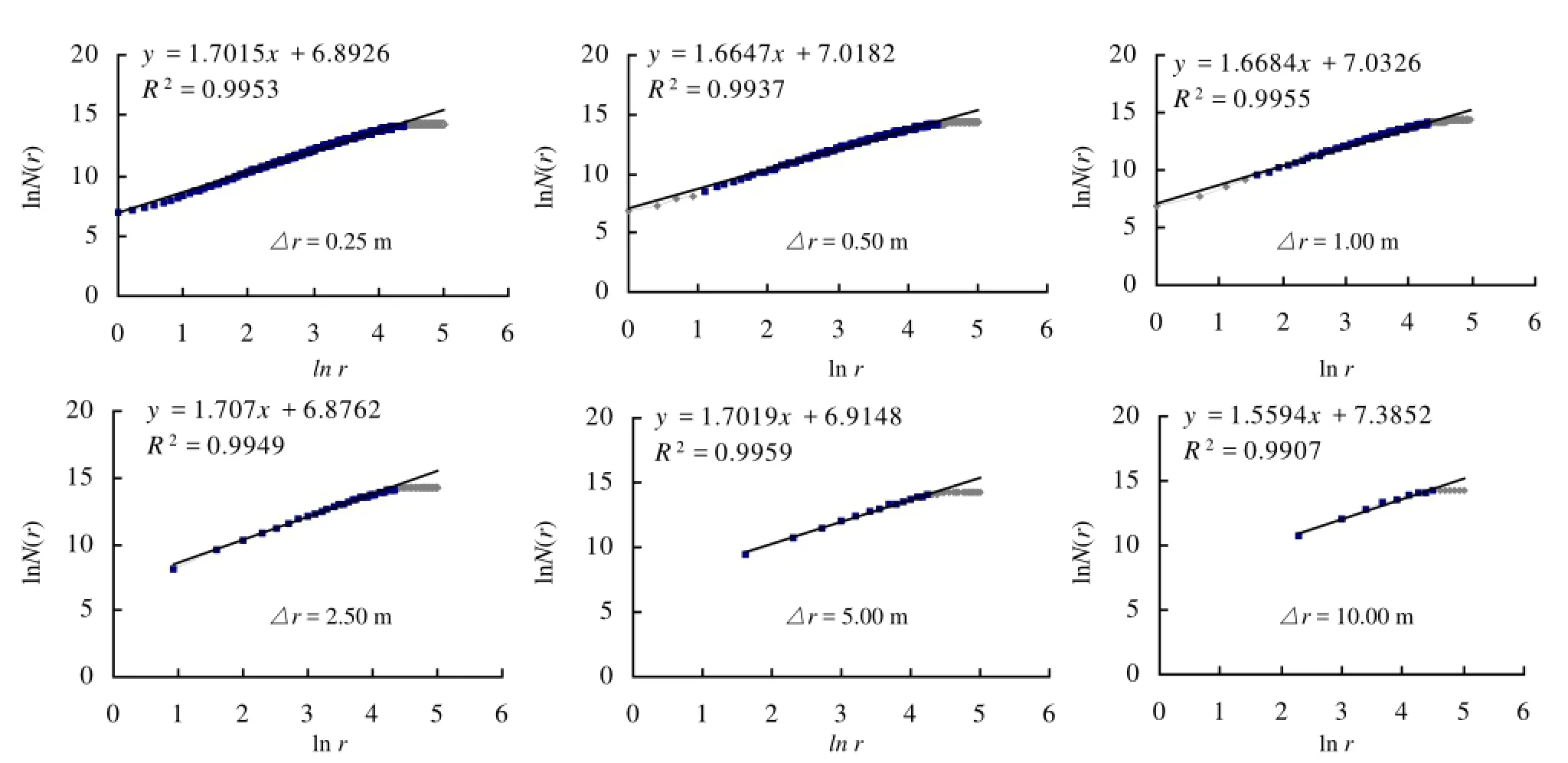
图2 步长△r= 0.25～10.00 m时D双对数线性回归图Figure 2 Step length△r= 0.25 – 10.00 m,DDoublelogarithmic linear regression

从图2中的散点图可以看出lnr和lnN(r)在一定区间内具有标度不变性的特点且具有线性关系。因此，在线性无标度区内采用最小二乘法进行线性回归。将回归后的关联维数和R2列在表8中。5.00 10.00 1.701 9 1.559 4 0.995 9 0.990 7

表8 不同步长下计算的关联维数Table 8 Correlation dimension calculated by different step length

从表8中可以看出，在不同步长下所有回归后所得的关联维数均接近于2且R2均大于0.990 7，回归为极显著。表明在不同的尺度下，本研究样区的树种在空间分布上为集聚分布。

4 结论

通过上述分析可得出如下结论：

（1）在天目山常绿阔叶林研究样区内，在不同步长下，其关联维数值在1.559 4～1.707 0。关联维数值波动范围很小且在该区域内趋于稳定，可以用来表征该区域的空间分布特征。

（2）关联维数接近于2，说明在该研究样区内的树木在空间分布格局上趋于集聚。

参考文献：

[1] 曹光球，林思祖，曹子林，等. 半天然杉阔混交林杉木及其伴生树种种群空间格局[J]. 浙江林学院学报，2002，19（2）：38－42.

[2] 曹永慧，萧江华，李迎春，等. 浙江天童披针叶茴香—南酸枣群落优势种群结构及空间格局[J]. 浙江林学院学报，2009，26（1）：44－51.

[3] 缪宁，刘世荣，史作民，等. 川西亚高山红桦—岷江冷杉林优势种群的空间格局分析[J]. 应用生态学报，2009（6）：1 263－1 270.

[4] 汤孟平，陈永刚，施拥军，等. 基于Voronoi图的群落优势树种种内种间竞争[J]. 生态学报，2007，27（11）：4 707－4 716.

[5] 张飞萍，蔡秋锦，卢凤美，等. 竹缺爪螨种群空间格局及时序动态[J]. 浙江林学院学报，2001，18（2）：61－64.

[6] 葛宏立，周元中，汤孟平，等. Ripley’s指数的一个新变形——G(d)[J]. 生态学报，2008，28（4）：1 491－1 497.

[7] 汤孟平，唐守正，雷相东，等. Ripley’s K（d）函数分析种群空间分布格局的边缘校正[J]. 生态学报，2003，23（8）：1 533－1 538.

[8] 张春雨，赵秀海. 随机区块法在空间点格局分析中的应用[J]. 生态学报，2008，28（7）：3108－3115.

[9] 岳文泽，徐建华，颉耀文. 甘肃城镇体系结构及其分形模型研究[J]. 地域研究与开发，2004，23（1）：16－20.

[10] 岳文泽，徐建华，司有元，等. 分形理论在人文地理学中的应用研究[J]. 地理学与国土研究，2001，17（2）：51－56.

[11] 梁士楚，董鸣，王伯荪，等. 红树植物木榄种群分布格局关联维数的研究[J]. 海洋科学，2003，27（6）：51－54.

[12] 马克明，祖元刚，倪红伟. 兴安落叶松种群格局的分形特征——关联维数[J]. 生态学报，1999，19（3）：65－70.

[13] 刘继生，陈彦光. 城镇体系空间结构的分形维数及其测算方法[J]. 地理研究，1999，18（2）：60－67.

[14] 党建武，王瑞玲，黄建国. 基于G. P算法的关联维计算中无标度区的识别[J]. 弹箭与制导学报，2003，23（1）：35－38.

[16] 陶冶，刘彤，贾亚敏，等. 古尔班通古特沙漠南缘心叶驼绒藜和梭梭种群空间格局的分形特征[J]. 干旱区地理，2008，31（3）：365－372.

[17] 汤孟平，周国模，施拥军，等. 天目山常绿阔叶林优势种群及其空间分布格局[J]. 植物生态学报，2006，30（5）：743－752.

[18] 杨洪晓，张金屯，李振东，等. 毛乌素沙地油蒿（Artemisia ordosica）种群空间格局对比[J]. 生态学报，2008，28（5）：1 901－1 910.

中图分类号：S718.54

文献标识码：A

文章编号：1001-3776（2010）04-0042-05

收稿日期：2010-03-03；修回日期：2010-05-14

基金项目：国家自然科学基金资助项目“基于GIS的森林空间结构调控研究”（30871963）；浙江省自然科学基金资助项目“基于GIS的毛竹林高产空间结构分析与优化调控模型研究”（Y3080261）；浙江林学院发展基金资助项目“利用差分法提高手持GPS定位精度”（2006FK28）

作者简介：陈永刚（1980－），男，内蒙兴和人，博士研究生，从事GIS在林业中应用开发工作。

Spatial Point Pattern Analysis on Fractal Correlation Dimension of Evergreen Broad-leaved Forest in Tianmu Mountain

CHEN Yong-gang1,2，TANG Meng-ping1，HU Yun2（1. School of Environmental Technology, Zhejiang A&F University, Lin’an 311300, China; 2. School of Information Engineering, Zhejiang A&F University, Lin’an 311300, China）

Abstract:Spatial point pattern analysis was conducted on evergreen broadleaved forest in Tianmu Mountain, Zhejiang province by fractal correlation dimension (D). First of all, a tree-tree distance matrix (Dn×n) was established in accordance with the coordinates of trees. Secondly, distance scale(r) of different step length(△r) and the number of treesN(r)of r was calculated according to theD. Finally, based on the calculation of the correlation dimensionD, the spatial point pattern of plant species in the tested area could be calculated. The results showed that point pattern of trees in the study area was clumped, and the correlation dimension could determine the spatial point pattern.

Key words:point pattern analysis; fractal; correlation dimension