双块式无砟轨道的共振性能分析
2010-05-08邹小魁吕定花
邹小魁,吕定花
(1.中铁山桥集团有限公司,河北 秦皇岛 066205;2.中铁山桥集团 高级技工学校,河北 秦皇岛 066205)
双块式无砟轨道断面的基本结构为基床表层(级配碎石)、混凝土支承层(C20混凝土)、道床板混凝土(C40混凝土)、双块式轨枕、钢筋桁架、扣件和钢轨[1],其断面见图 1。
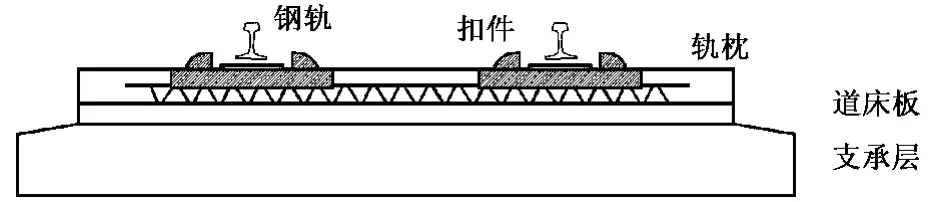
图1 双块式无砟轨道基本结构
双块式无砟轨道承受列车荷载的作用,在列车的激励下钢轨产生位移,并且当列车的激励频率与无砟轨道的固有频率一致时,将产生共振现象,使得钢轨位移过大而影响列车平稳性,加速轨道系统的损坏。因此采用谐响应分析方法,对无砟轨道系统共振频率进行计算分析,避免其产生共振就显得非常有意义。
1 谐响应分析模型建立的方法
谐响应分析是用于确定线性结构在承受随时间按正弦规律变化的荷载时的稳态响应,其目的是计算出结构在几种频率下的响应,并得到一些响应值(通常是位移)对频率的曲线,从这些曲线上可以找到“峰值”响应,并进一步观察峰值频率对应的应力。谐响应分析只计算结构的稳态受迫振动,而不考虑在激励开始时的瞬态振动。谐响应分析能预测结构的持续动力特性,从而克服共振、疲劳及其它受迫振动引起的不良影响。谐响应分析是一种线性分析,任何非线性特性如塑性和接触等,即使定义了也将被忽略[2]。
1.1 模型的完整性
应保证所建模型能反应出双块式无砟轨道各部分的振动模态,由于双块式无砟轨道应用于高速铁路,如选择较短的轨道模型将影响计算的精度,因此双块式无砟轨道的计算模型包含91根轨枕。
1.2 模型的精确性
本文采用有限单元法求解轨道共振频率,单元的细分程度决定了模型分析频率的高低,单元越细,分析频率越高。对1 000 Hz以内的分析频率,钢轨一跨轨枕间距划分为一个单元能满足精度要求,因此,双块式无砟轨道共振频率计算时,钢轨一跨轨枕间距至少应划分一个单元[3]。
根据以上所述,建立双块式无砟轨道谐响应分析模型,模型中,采用空间等截面梁模拟钢轨,轨枕采用变载面梁模拟,扣件系统简化成弹簧阻尼单元。
2 计算结果及分析
2.1 对既有双块式无砟轨道结构分析计算
在既有时速250 km/h和350 km/h的线路中,双块式无砟轨道已经被大量使用,分析计算时取和谐号动车组轴重17 t,考虑速度效应及偏载效应[3],轴重2倍的静轮载170 kN为加载荷载,阻尼比取0.05。时速250 km/h和350 km/h双块式无砟轨道扣件刚度分别为30 kN/mm和20 kN/mm。通过计算分别得到两种无砟轨道系统钢轨位移与频率曲线图,如图2、图3所示。

图2 250 km/h无砟轨道钢轨位移与频率曲线
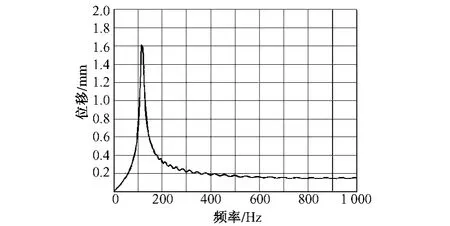
图3 350 km/h无砟轨道钢轨位移与频率曲线
由图2和图3可知,250 km/h和350 km/h两种双块式无砟轨道钢轨位移与频率曲线规律基本相同。在列车的激励频率与轨道系统一阶固有频率相同时,则发生共振现象,此时钢轨位移达到最大值;当列车的激励频率小于轨道系统的一阶固有频率时,钢轨位移随激励频率的增加而急剧增大;当列车的激励频率大于轨道系统的一阶固有频率时,钢轨的位移随着激励频率的增大而急剧减小;当激励频率 >400 Hz时,钢轨的位移趋于稳定状态。但是,250 km/h线路双块式无砟轨道共振频率和钢轨最大位移分别为143 Hz和1.50 mm,而350 km/h线路双块式无砟轨道共振频率和钢轨最大位移分别为115 Hz和1.61 mm。根据已有的研究成果显示:我国250 km/h客运专线的钢轨位移要求不大于2.0 mm,350 km/h客运专线的钢轨位移要求不大于 1.5 mm[4-5]。当共振现象发生时,350 km/h线路双块式无砟轨道系统钢轨位移大于建议的1.5 mm。
列车对轨道系统的周期激励主要来源于轨道不平顺波[3],轨道不平顺波是随机的,其不平顺波包含许多不同的波长成分,而0.01~200 m波长的不平顺最为常见。其中波长在1 m及以下的不平顺主要是钢轨波纹或波浪形磨耗,是一种周期性不平顺。根据以上两种轨道系统的共振频率计算可知,对于250 km/h双块式无砟轨道应避免486 mm的波长存在,对于350 km/h双块式无砟轨道应避免846 mm的波长存在。
2.2 扣件系统刚度对双块式无砟轨道系统的影响
保持以上条件不变,仅改变双块式无砟轨道扣件系统刚度,考察系统共振频率、钢轨最大位移的变化规律。通过计算可得扣件系统刚度与共振频率关系曲线如图4所示,扣件系统刚度与钢轨最大位移关系曲线如图5所示。
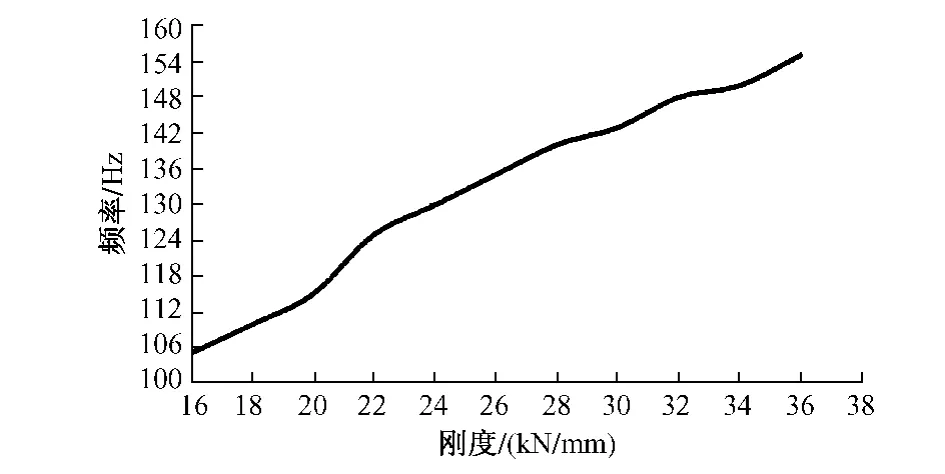
图4 扣件刚度与共振频率关系曲线
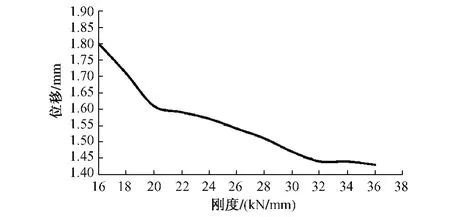
图5 扣件刚度与钢轨最大位移关系曲线
由图4可见,双块式无砟轨道的共振频率与扣件刚度大体上呈线性增长关系。扣件刚度为16 kN/mm时,共振频率为 105 Hz,而当扣件刚度增加到 36 kN/mm时,共振频率增加到 155 Hz,其增长斜率为2.5。双块式无砟轨道的共振频率是轨道系统的一种固有特性,不随外界条件的改变而改变,若要改变轨道系统的共振频率可通过改变扣件刚度的方法来实现。由图5可知,钢轨的最大位移随着扣件刚度的增大而减小,当扣件刚度为16 kN/mm时,钢轨的最大位移为1.80 mm,当扣件刚度为36 kN/mm时,钢轨的最大位移为1.43 mm,减小了20.5%。但由于其钢轨最大位移基数较小,位移变化不明显。
2.3 列车荷载对双块式无砟轨道系统的影响
以250 km/h客运专线采用的双块式无砟轨道为研究对象,在列车荷载变化的条件下,考察双块式无砟轨道系统共振频率、钢轨最大位移的变化规律。通过计算可得列车荷载与双块式无砟轨道共振频率关系如图6所示,列车荷载与钢轨最大位移关系如图7所示。
由图6可知,对于双块式无砟轨道系统,列车荷载对其共振频率没有任何影响,无砟轨道系统一经建成,其共振频率就已经确定,不随外界条件的变化而变化。由图7可以看出,钢轨的最大位移随着荷载的增大而呈线性增长,当荷载为130 kN时,钢轨最大位移1.12 mm,荷载为270 kN时,钢轨的最大位移增加了108%,达到2.34 mm,可见荷载的增大将急速加剧钢轨最大位移的增大,这将导致钢轨应力的增大,加速轨道系统的损坏,因此应严格控制列车的轴重。
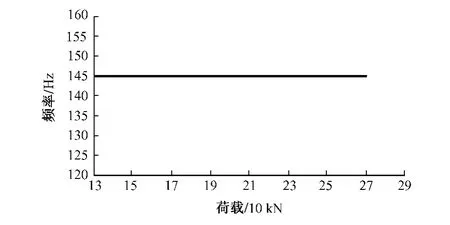
图6 荷载与频率关系曲线
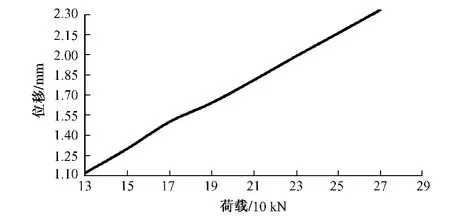
图7 荷载与钢轨最大位移关系曲线
2.4 阻尼对双块式无砟轨道系统的影响
客运专线双块式无砟轨道的阻尼反映了其结构对列车冲击能量的耗散性能,这里主要考虑系统扣件阻尼的影响,将扣件刚度保持在20 kN/mm不变,计算扣件阻尼比为0.01~0.09时,双块式无砟轨道系统共振频率、钢轨最大位移的变化规律,图8及图9为计算结果。
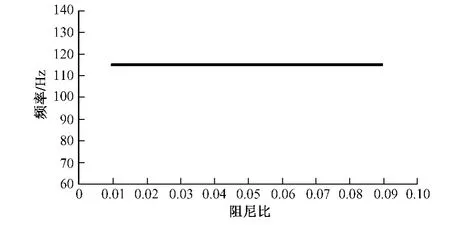
图8 阻尼比与频率关系曲线
由图8可以看出,阻尼比对轨道系统的共振频率没有任何影响。图9表明,钢轨最大位移随着阻尼比的增加而减小,当阻尼比为0.01时,钢轨最大位移为3.45 mm,当阻尼比为 0.09时,钢轨的最大位移为1.08 mm,减小了68.7%。可见阻尼能够有效地减小钢轨的位移及应力,保护轨道系统的稳定性。
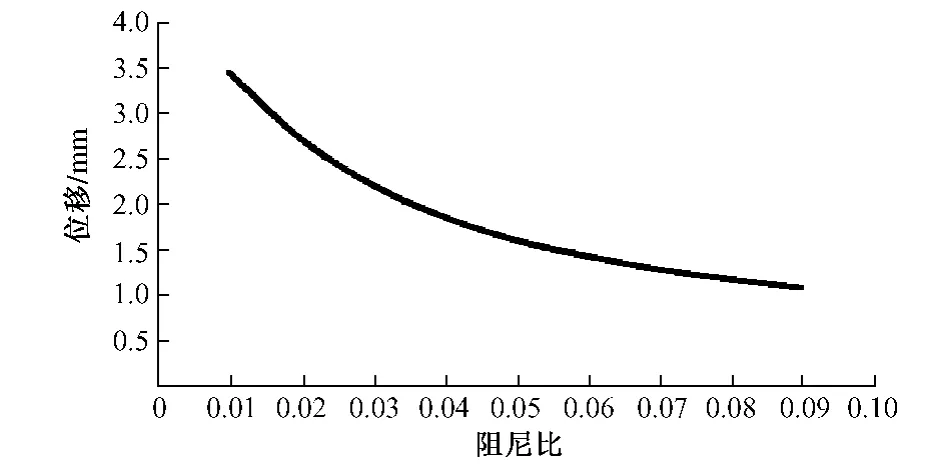
图9 阻尼比与钢轨最大位移关系曲线
3 结论
1)列车激励频率达到双块式无砟轨道系统共振频率时,钢轨的位移及应力最大,因此在实际线路运营中应避免轨道系统产生共振现象,即对于250 km/h双块式无砟轨道应避免486 mm的波长存在,对于350 km/h双块式无砟轨道应避免846 mm的波长存在。
2)时速250 km/h客运专线双块式无砟轨道在共振点时钢轨位移满足位移最大建议值,而时速350 km/h客运专线双块式无砟轨道在共振点时钢轨位移大于位移最大建议值。因此,应对扣件刚度进行进一步的优化设置,可通过增大扣件刚度值到25 kN/mm解决此问题。
3)列车荷载及阻尼不影响双块式无砟轨道的共振频率,而仅影响钢轨的位移及应力;列车荷载增大,钢轨位移及应力增大;阻尼增大则钢轨位移及应力减小。
4)与列车荷载及阻尼相比较,改变扣件系统刚度则改变双块式无砟轨道的共振频率和钢轨的位移及应力。扣件系统刚度增大,轨道系统共振频率增加,钢轨位移及应力减小。
[1]刘振民,钱振地,张雷.双块式无砟轨道道床板混凝土裂缝的分析与防治[J].铁道建筑,2007(6):99-101.
[2]王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社,2007.
[3]陈小平.高速道岔轨道刚度理论及应用研究[D].成都:西南交通大学,2008.
[4]崔国庆.双块式无砟轨道合理刚度取值研究[J].铁道建筑,2009(9):93-95.
[5]陈骁文.双块式无砟轨道施工工艺及施工精度控制[J].铁道建筑,2009(2):108-110.
