CRTSⅠ型板式轨道在地震荷载作用下的动力响应

宋 杨，张 瑶，陈小平，王 平

(西南交通大学 土木工程学院，成都 610031)

板式无砟轨道具有良好的结构连续性和平顺性，并且结构稳定、耐久性好，在低等级地震条件下，比有砟轨道具有更好的稳定性，从而提高行车的安全性，但在大地震情况下，有砟、无砟轨道都会遭到破坏，而无砟轨道的修复更为困难。日本对有砟轨道的研究表明，地震造成轨道破坏与变形的原因，大体上可以分为两类:路基、桥梁等下部基础破坏及变形，轨道本身破坏与变形，但对于无砟轨道尚无法判断其破坏的原因，也没有相应的抗震设计规范作为指导，所以对其破坏的原因进行分析具有十分重要的意义。

CRTSⅠ型板式轨道广泛应用于遂渝试验段地震频发线路，对CRTSⅠ型板式无砟轨道进行地震荷载下的动力响应分析很有必要。目前的抗震分析方法主要是原型观测、模型试验和理论计算数值分析方法。而理论计算数值分析方法亦有很多种，其中以有限元技术最为成熟。本文运用有限元软件ANSYS，采用地震反应时程分析法，模拟地震对CRTSⅠ型板式轨道的作用，地震荷载采用天津波南北方向记录，并得出此荷载作用下轨道板、底座板、CA砂浆和圆形凸台的位移、加速度和应力。

1 计算模型及参数

1.1 计算模型

轨道各结构直接生成有限元模型，轨道板与底座板由于在其厚度方向上的尺寸远小于长度和宽度方向上的尺寸，符合弹性薄板的结构特点，故均采用平面壳单元模拟;为了模拟土体、砂浆和树脂的单向受力特性，CA砂浆、地基土层和凸台周边树脂均采用非线性杆单元模拟;圆形凸台采用梁单元模拟，并且约束在底座板上。为消除边界效应，模型选取三块轨道板进行计算，以中间单元板作为研究对象。路基底面采取全约束，两侧采用对称约束。动力计算模型如图1所示。

图1 CRTSⅠ型板式轨道计算模型

1.2 计算参数

轨道板长×宽×厚为4.962 m×2.400 m×0.190 m，采用 C50混凝土，弹性模量为34 500 MPa，密度为2 800 kg/m3;CA砂浆宽 ×厚为2.4 m×0.05 m，弹性模量取300 MPa，密度为1 800 kg/m3。底座板宽 ×厚为3 m×0.2 m，采用 C40混凝土，弹性模量为34 000 MPa，密度为2 800 kg/m3;基床采用等刚度换算:取路基高1 m，弹性模量为 30.64 MPa，密度为2 000 kg/m3，阻尼比为5%;凸台周边树脂宽 ×厚为2.4 m×0.05 m，弹性模量取 25 MPa，密度为 150 kg/m3，阻尼比为10%。

1.3 地震波荷载

模型计算中地震波荷载烈度分别取6度、7度和8度时，其地面运动的最大水平加速度分别为0.062 5g、0.125 g和0.250 g，计算中必须将实际地震记录的峰值折算成所需的基本烈度。地震波采用天津波南北向记录，地震波的记录时长为6 s，时间间隔为0.01 s，场地为三类，记录信号为南北向加速度。竖向最大加速度约为水平最大加速度的0.50～0.65倍，因此可取竖向与水平地震系数之比为0.65。

2 计算结果及分析

2.1 动应力响应

在地震荷载作用下，轨道板在各地震烈度下的横向应力响应如图2所示，底座板在各地震烈度下的竖向应力响应如图3所示。

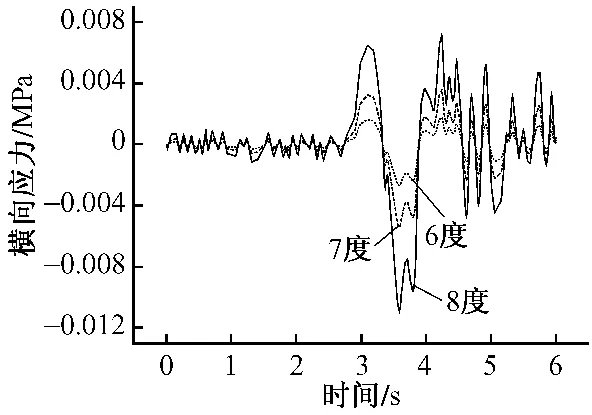
图2 轨道板横向应力响应

图3 底座板竖向应力响应

图2表明，轨道板不同烈度横向应力响应曲线形状相似，极值响应时间基本一致。地震烈度为6度、7度、8度时，轨道板的最大动拉应力、动压应力基本呈2倍关系递增，具体数值见表1。地震烈度为8度时，轨道板的最大动拉应力为0.007 13 MPa，最大动压应力为0.010 9 MPa，远小于轨道板中混凝土的抗拉、抗压破坏强度，不会对轨道板造成破坏。底座板和CA砂浆的横向应力响应具有与轨道板同样的变化规律，也不会使结构破坏。

图3表明，在各烈度地震荷载作用下，底座板竖向应力响应曲线形状相似，极值响应时间也基本一致。由于受初始压应力的影响，底座板最大压应力普遍大于最大拉应力，具体数值见表1。烈度为8度时，底座板的最大动拉应力为0.020 5 MPa，最大动压应力为0.032 5 MPa，远小于底座板中混凝土的抗拉、抗压破坏强度，不会对底座板造成破坏。底座板横向应力响应具有与轨道板同样的变化规律，也不会使结构破坏。

CA砂浆、圆形凸台动应力在地震荷载作用下的时间历程曲线如图4、图5所示。

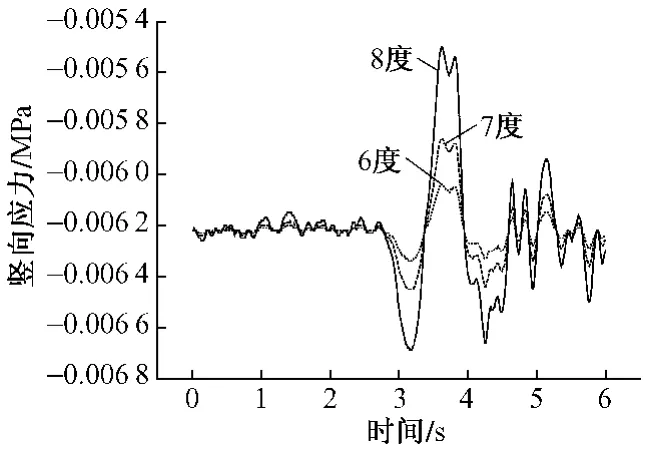
图4 CA砂浆垂向应力响应

图5 圆形凸台应力响应

图4表明，CA砂浆由于受初始压应力影响，一直受压，并且幅值变化很小，说明砂浆弹性良好，能较好地缓冲地震波影响。图5表明，由于凸台周边树脂阻尼比较大，对圆形凸台起到良好的保护作用，凸台在各烈度地震波作用下，受力也较小。CA砂浆、圆形凸台各烈度地震波下最大动应力响应见表1。

表1 地震荷载作用下轨道结构最大动应力值 MPa

2.2 动位移响应

铁路路基、轨道结构在地震荷载作用下的位移较大，但影响轨道结构稳定性的主要是其相对于下部路基的位移，这也是论文中对动位移分析的主要内容。图6、图7分别表示在各烈度地震荷载作用下，底座板竖向位移响应曲线和轨道板横向位移响应曲线。

图6 底座板竖向位移响应

图7 轨道板横向位移响应

图6、图7表明，不同烈度底座板竖向、轨道板横向位移响应曲线形状相似，极值响应时间基本一致，并且都是随着地震烈度提高，其位移极大值增加一倍，说明没有破坏时的轨道结构变形具有一定的规律性。地震烈度为8度时，底座板竖向位移最大为0.102 mm，轨道板横向位移最大为0.782 mm，其数值较小，对轨道几何形位的影响不明显，但随着高速铁路运行速度的不断提高，势必会影响列车运行的稳定性，建议地震过后对列车运行速度进行限制。

图8表示在地震荷载作用下，两相邻轨道板横向错牙量响应曲线。

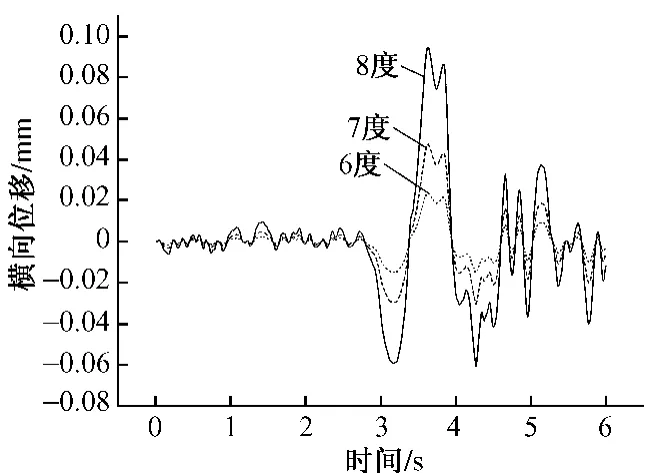
图8 两相邻轨道板横向错牙量响应

图8表明，不同烈度地震荷载作用下，两相邻轨道板横向错牙量都很小，递增趋势同轨道板横向位移。8度地震荷载作用下，最大横向错牙量为0.095 mm，远小于现行规范中规定值，对轨道几何形位的影响不明显。

3 结论

本文借助ANSYS软件，建立CRTSⅠ型板式轨道有限元模型，并对模型进行不同地震烈度荷载下的时程分析，得到板式轨道结构中轨道板、底座板、CA砂浆和圆形凸台的动应力、动位移的响应规律。主要得到以下结论:

1)在地震荷载作用下，轨道结构横向应力和纵横向位移响应随烈度增加1度而增加1倍;竖向应力响应由于受初始应力影响，压应力较大。总体来说，轨道结构最大动应力较小，不会使轨道结构破坏。

2)轨道结构横向位移响应大于竖向位移响应，轨道结构位移响应对轨道几何形位有一定影响，建议地震后对列车行驶速度进行限制。

3)在路基稳定的情况下，板式轨道本身变形及受力很小。板式轨道结构本身的变形不会是导致轨道结构破坏或变形的原因。

［1］詹永祥，蒋关鲁，魏永幸.无砟轨道桩板结构路基在地震荷载下的动力响应分析［J］.中国铁道科学，2006，27(6):22-26.

［2］王伟华，李培刚，杨荣山，等.树脂板式轨道地震动力响应分析［C］//高速铁路线路工程设计、施工及养护技术国际学术会议论文集，2009:113-117.

［3］王其昌，韩启孟.板式轨道设计与施工［M］.成都:西南交通大学出版社，2002.

［4］中华人民共和国国家标准.GB 50011—2001 建筑抗震设计规范［S］.北京:中国建筑工业出版社，2001.

［5］李国强，李杰.建筑结构抗震设计［M］.北京:中国建筑工业出版社，2006.

［6］王涛.高速铁路板式无砟轨道 CA砂浆的研究与应用［D］.武汉:武汉理工大学，2008.

［7］沈聚敏，周锡元.抗震工程学［M］.北京:中国建筑工业出版社，2000.

［8］赵国堂.高速铁路无砟轨道结构［M］.北京:中国铁道出版社，2006.

［9］佐藤吉彦.新轨道力学［M］.北京:中国铁道出版社，2001.