交通荷载作用下风积沙路基动力响应分析
2010-05-08黄俊文杨长卫周新文
黄俊文,马 涛,杨长卫,周新文
(1.中铁二局集团有限公司 建设管理公司,成都 610032;2.西南交通大学 土木工程学院,成都 610031;3.南宁铁路局,南宁 530003)
现行路面及路基设计方法采用竖向静载作用下弹性多层体系的理论模型,与实际情况不符,道路上行驶的车辆对路基产生的振动作用随时间和道路表面特征的变化而变化,是一个典型的动力荷载。随着我国经济建设和交通运输事业的发展,车流量、行车速度和载重量不断增加,交通荷载对路面、路基的影响也越来越大,路面、路基设计理论由静态体系发展为动态体系已成为必然趋势[1~4]。研究交通荷载下风积沙路基的动力响应将为分析交通荷载下风积沙路基的动应力、加速度、塑性应变及永久变形的变化规律提供依据,以便能够进一步把握路基路面结构发生破坏的各种控制因素及发育机制,避免路基出现过量变形;同时对检验和完善风积沙路基的设计施工,推动沙漠地区高速公路建设都具有深远的意义。本文采用FLAC3D数值分析方法探讨交通荷载作用下风积沙路基的动力响应。
1 风积沙基本特性
1.1 风积沙粒径组成
风积沙的粒径组成由筛分试验确定,试验结果如表1所示。沙样1和沙样2都是取自榆神高速公路沿线具有代表性的风积沙,沙样3是由沙样1和沙样2混合而成,三种砂样的颗粒级配曲线见图1。
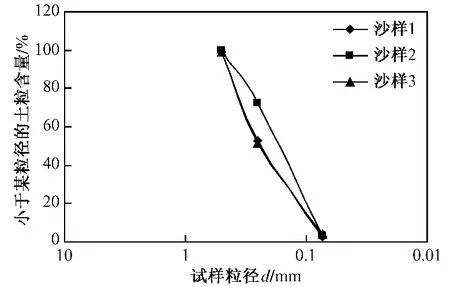
图1 三种沙样的颗粒级配曲线

表1 风积沙筛分试验结果
由表1可知,在风积沙的粒径组成中,其颗粒粒径主要分布在0.500~0.074 mm范围内,占总颗粒含量的96.4%;2.00~0.50 mm的颗粒含量占总颗粒含量的0.43%;<0.074 mm颗粒的含量占总颗粒含量的4.10%,从而可计算出沙粒的细度模数。
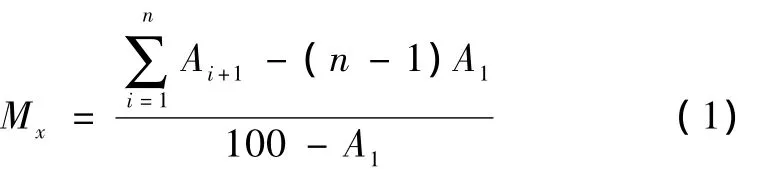
式中,Ai为各孔径的累计百分数;Mx为风积沙细度模数;A1为第一级孔径累计百分数。
通过计算得:Mx=1.28,均方差 0.31,变异系数0.23,属极细沙。
根据式(2)可计算不均匀系数Cu和曲率系数Cc为
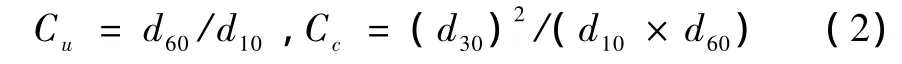
式中,d10,d30,d60分别为沙样中小于该粒径的颗粒含量为10%、30%和60%的粒径(mm)。
由此可知,对于沙样1,Cu=3.45,Cc=0.98;对于沙样 2,Cu=2.35,Cc=0.85;对于沙样 3,Cu=3.45,Cc=1.11。试验结果说明,风积沙级配不良,沙粒均匀,根据规范有关对土的分类,这种风积沙属于级配不良的细沙,见表1。
1.2 风积沙的天然含水量、干密度和相对密度
由于沙的蓄水能力低,而且沙漠地区降雨量又小,因此风积沙的天然含水量很低,一般在1.4% ~3.3%之间,迎风坡及坡谷的含水量最大,为3.2% ~3.3%,坡峰为2.3%,背风坡最小,为1.4%。不同位置风积沙的天然干密度也不尽相同,坡峰的天然干密度较大,迎风坡、坡谷和背风坡表面风积沙的干密度较低。根据对榆神高速公路沿线风积沙的天然干密度、含水量现场调查,风积沙的天然干密度在1.43~1.48 g/cm3之间,20 cm以上天然含水量在1.2% ~3.4%之间,20 cm以下含水量在3.2% ~3.8%之间[5]。
土粒相对密度是土的基本物理指标之一,是计算孔隙比和评价土类的主要指标,风积沙的相对密度与土中所含矿物的相对密度和含量有关,相对密度越大,颗粒越粗,沙粒之间排列紧密,天然密度较大,反之则天然密度较小,风积沙的相对密度一般为2.61~2.67。
2 交通荷载的模拟
交通荷载对路面的作用会因为车型、车速的不同而不同,车辆荷载大小及作用频率都是呈动态变化的,要准确模拟比较困难。Hyodom等通过将10 t的卡车作为交通荷载以 0、10、20、30、35 km/h 的不同速度在试验路面上往复运动,得到了交通荷载作用下地基不同深度处的竖向土压力。就地基中某一点而言,竖向土压力p的波形如图2所示,可采用半波正弦加载曲线来描述[6]。

图2 车辆荷载加载波形
车辆动荷载对某一点的作用可简化为
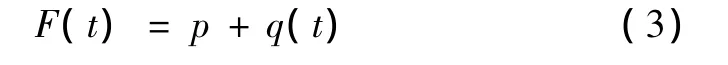
式中,p为恒载,大小等于轮压;q(t)为附加动荷载,变化规律采用黄仰贤[7]在 Kenlayer程序中给出的简化形式,车辆附加动荷载对某一点的作用等效为正弦分布荷载。

式中,qmax为车辆附加荷载的幅值;T为荷载作用周期;L为轮胎接触面积半径,一般取15 cm;V为车辆行驶速度。
变换式(4),将荷载作用时间转换到[0,T]区间上,可得

动荷系数与路面不平整度和车速有关,路面较平整且车速不太大时,一般不超过1.3,若取动荷系数为1.2,则 qmax=0.2p,最后得到的车辆荷载为
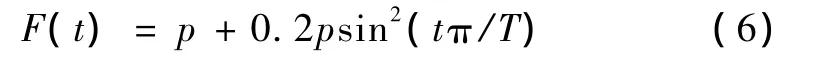
3 模型的建立和计算参数的选择
图3为本文计算的几何模型,图4为几何模型在FLAC3D中的实现及网格划分。表2为数值模拟采用的计算参数,表3为交通荷载输入参数。采用半波正弦加载,荷载作用位置为距道路中心线9.5 m处和11.5 m处。

图3 风积沙路基几何模型(单位:cm)

图4 几何模型在FLAC3D中的实现
4 数值模拟结果分析
4.1 永久位移
图5为路基不同深度处永久位移随重复荷载作用次数变化曲线。可见在车辆荷载作用下,风积沙路基不同深度处的永久位移都随着重复作用次数的增加而增加,但变形的增长速度则随着重复荷载作用次数的增加而降低并逐渐达到稳定。加载初期,路基体颗粒之间相互靠近,孔隙变小,两测点的位移增加较快;随着加载次数的增加,在动应力的作用下,路基体被逐渐压密,位移增量逐渐减小;当加载到一定次数后,在路基体动应力作用下,只发生弹性变形,位移基本稳定。
1)永久位移随深度的变化
图6为风积沙路基不同位置的永久位移随深度的变化曲线。从图6中可以看出,加载1 000个周期后风积沙路基的最大位移值是2.5 mm左右,永久位移随深度的增加非线性衰减。
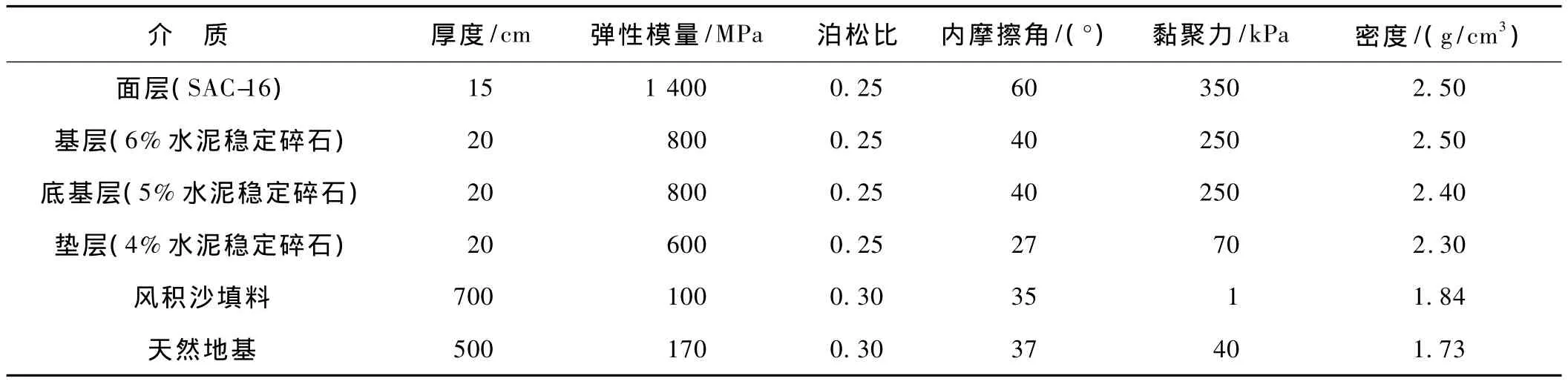
表2 数值模拟采用的计算参数

表3 交通荷载输入参数
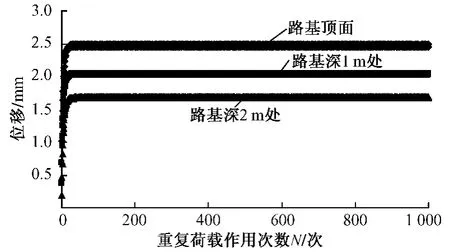
图5 路基不同深度处永久位移随重复荷载作用次数变化曲线
2)永久位移沿横向的变化
图7为不同深度位置路基产生的位移在横向上的变化曲线。从图7可以看出,在相同深度处,车辆轮胎作用位置,路基产生的沉降最大,并向轮胎两侧衰减扩散。
4.2 动应力
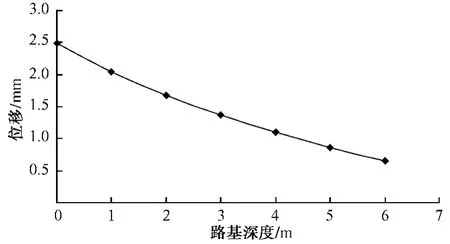
图6 风积沙路基不同位置的永久位移随深度变化曲线
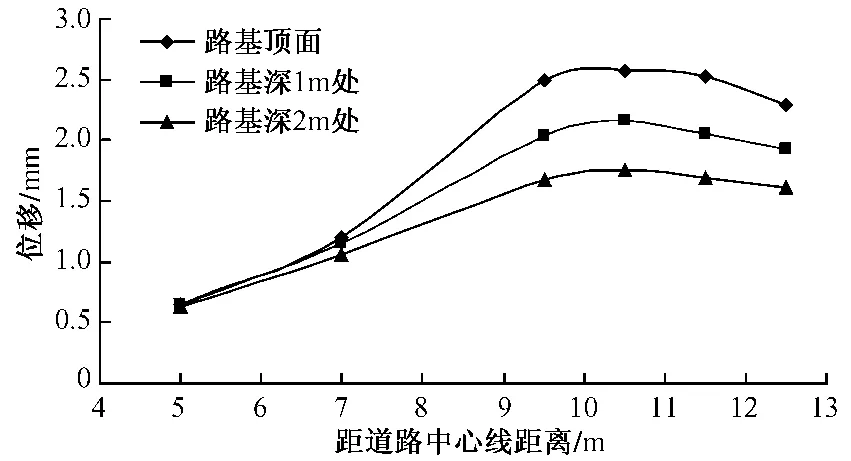
图7 不同深度位置路基产生的位移在横向上的变化曲线
图8为路基不同深度处动应力随重复荷载作用次数变化曲线。可见风积沙路基在不同深度附加应力都随着重复荷载作用次数的增加而增加,但增加速度则随着重复荷载作用次数的增加而降低并逐渐稳定。随着循环加载次数的增大,土体中的动附加应力均呈现累积的趋势,表现出典型的动附加应力累积效应。

图8 路基不同深度处动应力随重复荷载作用次数变化曲线
1)动应力沿路基深度的变化
图9为动应力随路基深度的变化曲线。路基中所产生的动应力随着深度的不断增加而急剧地衰减。

图9 动应力沿路基深度的变化曲线
2)动应力沿路基横向的变化
图10为路基不同位置动应力沿路基横向的变化规律曲线。从图10可以看出,在同一深度处,车轮处动应力最大,并向两侧衰减扩散。
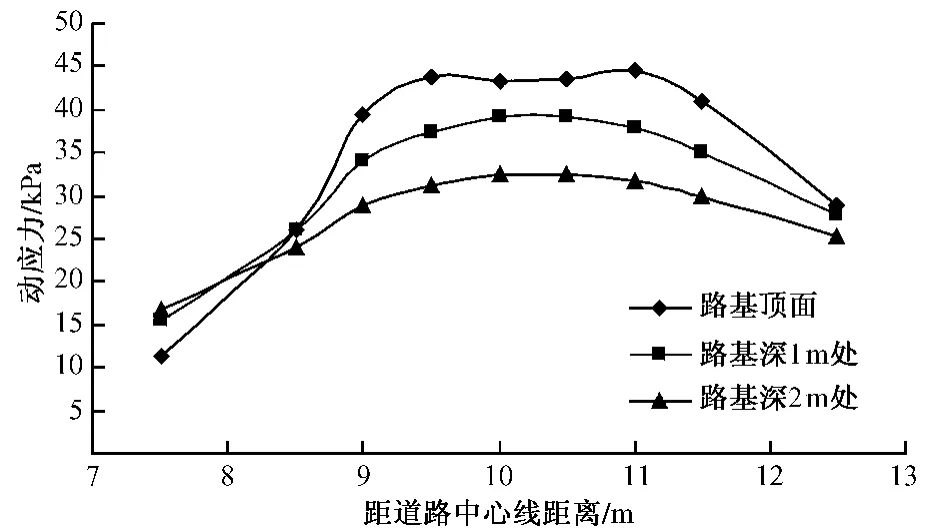
图10 路基不同位置动应力沿横向的变化规律曲线
4.3 竖向加速度
图11为竖向加速度峰值随路基深度的变化曲线。加速度是反应动荷载对路基土体影响的重要指标,加速度的变化规律可以反映出汽车对路基振动作用的情况。随着路基深度的增加,加速度峰值急剧减小。在路基顶部,加速度峰值约为24.87 cm/s2;而在1 m深度处后加速度骤降为 8.3 cm/s2,加速度值衰减了66.7%。当深度进一步增加,加速度峰值逐渐减小。
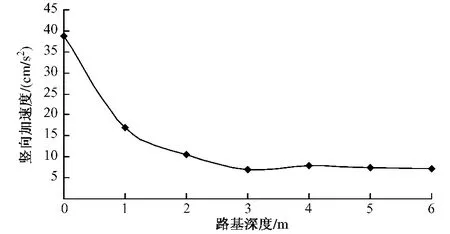
图11 竖向加速度峰值随路基深度变化曲线
5 结论
1)风积沙路基在不同深度的永久位移都随着重复荷载作用次数的增加而增加并逐渐稳定;风积沙路基的永久位移随深度的增加非线性衰减;在路基横向上,车辆轮胎作用位置,路基产生的沉降最大,向轮胎两侧衰减扩散。
2)风积沙路基在不同深度动应力都随着重复荷载作用次数的增加而增加并逐渐达到稳定。随着循环加载次数的增大,土体中的动应力均呈现累积的趋势,表现出典型的动附加应力累积效应。
3)动应力沿深度的增加迅速衰减,在路基横向上,车轮处动应力最大,并向两侧衰减扩散。
4)竖向加速度随着路基深度的增加,其峰值急剧减小。
[1]廖化荣.红黏土路基循环动荷载下塑性力学行为及预测模型研究 [D].广州:中山大学,2004.
[2]汤连生,张庆华,尹敬泽,等.交通荷载下路基土动应力应变累积的特性[J].中山大学学报(自然科学版),2007,46(6):143-144.
[3]张庆华.交通荷载下路基土应力—应变量化模型及工后沉降预测研究[D].广州:中山大学,2007.
[4]廖化荣.交通荷载下路基软土动应力累积及塑性应变累积特性研究[D].广州:中山大学,2008.
[5]俞利宾.冲击振动压路机模型对风积沙压实试验研究[D].西安:长安大学,2009.
[6]HYODO M,YASUHARA K. Analyticalprocedurefor evaluating pore-water pressure and deformation of saturated clay ground sub-jected to traffic loads[C]//Proceedings of the 6th International Conference on Numerical Methods in Geomechanics Inns-bruck,1987:653-658.
[7]黄仰贤(美).路面分析与设计[M].北京:人民交通出版社,1998.
