层次分析法在编组站建设项目中的应用研究

刘 晶

（北京全路通信信号研究设计院，北京 100073）

在编组站建设项目中，常常遇到项目实施方案如何选择的问题。需要从方案的安全性、可靠性、经济性、技术难度等因素综合考虑。而这些参考因素的不可量化给方案的选择带来了困难。特别是铁路建设项目，如果强调方案的安全性与可靠性，则势必降低作业效率；反之，如果过度提高作业效率，则必然影响安全性。如何综合考虑这些相关因素，选择出最适合项目的实施方案，需要采用一套科学的管理方法。层次分析法可以将不可量化的指标用两两比较的方法进行比较，从而选择出最适合的方案，从一定程度上解决这些问题。

层次分析法（AHP），是20世纪70年代美国学者T.L.Saaty提出的，是一种强有力的系统分析运筹学方法，在经济学、管理学中有广泛应用。层次分析法对多因素、多准则、多方案的综合评价及趋势预测相当有效。层次分析法将待解决的问题根据“方案层—因素层—目标层”构成的递阶层次结构决策分析，给出了一整套处理方法与过程。层次分析法最大的长处是可以处理定性与定量相结合问题，可以将无法量化的因素按照重要度排序，并将决策者的主观判断与积累的经验导入模型，加以量化处理，从而得到最终的决策结果。

层次分析法处理问题的基本步骤如下。

第一步，确定评价目标，明确方案评价的准则。根据评价目标、评价准则构造递阶层次结构模型。

第二步，应用两两比较法构造所有的判断矩阵。

第三步，确定项目构成要素的相对重要度。

第四步，计算综合重要度。

下面用一个例子详细说明层次分析法在实际项目中的用法。假定现有一个编组站需要建设站内专用无线网络，要求网络无线信号能够覆盖整个站场，面积约为2 km×6 km的近似矩形区域，站场内无大型障碍物遮挡信号，并要求无线通信带宽≥2 M，速率≥100 kbits/s，站内无线接入终端在10个以上。现有3个备选技术方案，需要综合成本因素、实施难度、通信效果和后期维护几个方面对方案进行分析，确定最佳方案。方案一，选用WLAN通信技术；方案二，选用McWill通信技术。应用层次分析法对这两个方案进行比较。

1 构造递阶层次结构模型

递阶层次结构模型一般分为3层：（1）目标层：最高层次，或称理想结果层，是指决策问题所追求的总目标；（2）准则层：评价准则或衡量准则，是指评判方案优劣的准则，也称因素层、约束层；（3）方案层：也称对策层，是指决策问题的可行方案。各层间诸要素的联系用弧线表示。

本例中目标层应为“最佳通信方案”；准则层应为“成本因素”、“实施难度”、“通信效果”、“后期维护”等几个决定因素；方案层即为本例中的两个技术方案。构造本例的递阶层次结构模型如图1所示。

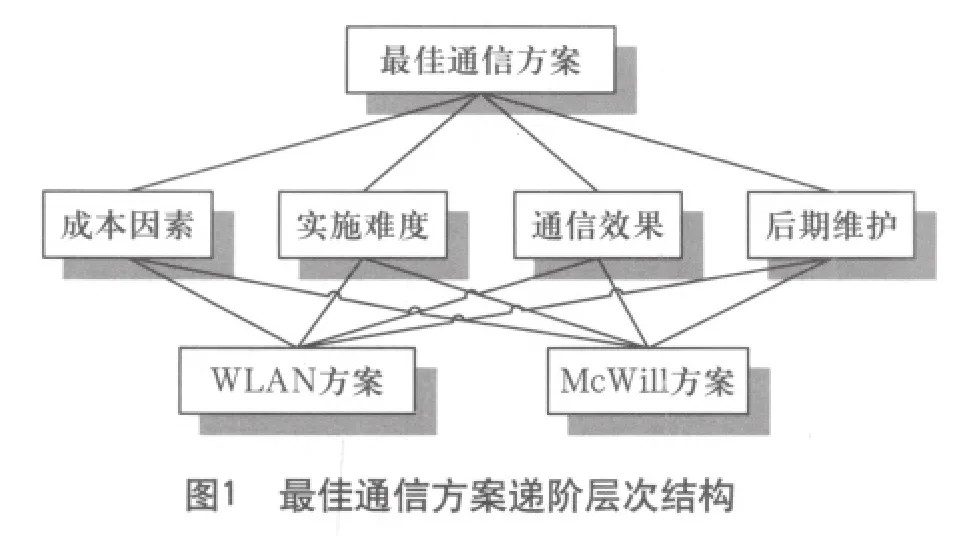
2 构造判断矩阵

应用两两比较法构造判断矩阵首先应确定判断尺度。判断尺度如表1所示，表中的判断尺度表示要素Ai对要素Aj的相对重要性的数量尺度。

表1 两两比较法标度

建立判断矩阵。判断矩阵是以上层的某一要素Hs作为判断标准，对下一层要素进行两两比较确定的元素值，例如在Hs准则下有n阶判断矩阵A（aij），其形式如表2所示。

表2 n阶判断矩阵A示意

判断矩阵中的元素aij表示从判断准则Hs的角度考虑要素Ai对要素Aj的相对重要性，即aij=Wi/Wj，显而易见判断矩阵A有：aij＞0，aij=1/aji，aii=1。

根据判断准则建立本例各级判断矩阵。建立“最佳通信方案”的判断矩阵，将决定最佳通信方案的4个要素进行两两比较。首先，成本对于实施难度而言，只要在方案可以实施的前提下，成本更低的方案更适合项目，因此，成本的重要度要略高于实施难度，将此判断结果设置为2；其次，成本对于通信效果而言，显然通信效果更为重要，因此应将此判断结果设置为1/5；最后，成本相对于后期维护，虽然后期维护工作量的多少会影响到方案的总体成本，但建设成本的重要度要略高于后期维护，将此判断结果设置为3。依次类推，分别设置其余因素两两比较的相对重要度，得到最佳通信方案判断矩阵，如表3所示。

表3 最佳通信方案判断矩阵

分析方案层。该层有两个方案，分别是WLAN技术和McWill方案。分别在成本因素、实施难度、通信效果和后期维护4个方面对两个方案进行比较。建立判断矩阵A1～A4，如下所示。

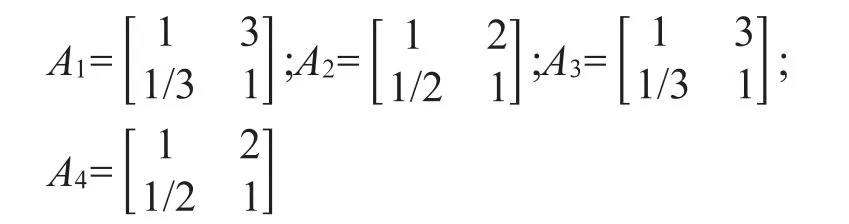
3 计算判断矩阵并确定项目决定因素的相对重要度

分别计算判断矩阵A，A1，A2，A3，A4的特征向量，分别用W，W1，W2，W3，W4表示。首先计算矩阵A的特征向量W。

（1）计算A的各行之和

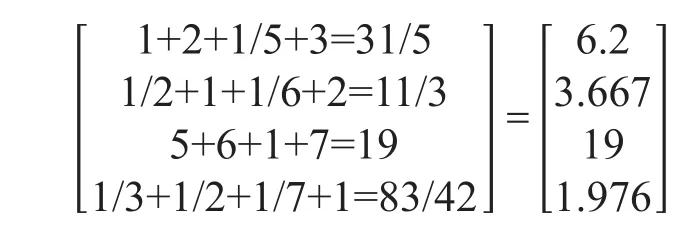
（2）计算各行平均值，因为A有4列，所以求平均值时用3除各行之和

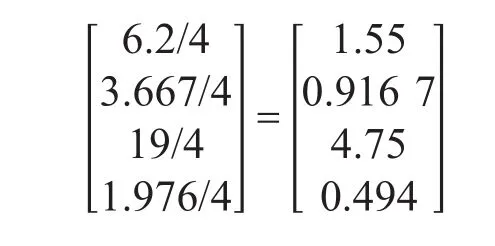
（3）归一化，即将各行除以4行之和（1.55+0.916 7+4.75+0.494=7.710 7），得到矩阵A的 特征向量W

根据该计算结果，在本例中通信效果最重要（占0.616 0），成本因素其次（占0.201 0），实施难度第三（占0.118 9），后期维护第四（占0.064 1）。

同样，计算矩阵A1～A4的特征向量W1～W4，计算结果如下。

W1表明，从成本角度考虑WLAN方案更经济；W2表明，从实施难度考虑WLAN方案更容易；W3表明，从通信效果考虑McWill方案效果更好；W4表明，从后期维护角度考虑，WLAN方案更容易维护。

（4）一致性检验

在对系统要素进行相对重要性判断时，由于运用的主要是专家的隐性知识，不可能完全精密的判断出Wi/Wj的比值，只能对其进行估计，因此，必须进行相容性和误差分析。估计误差必然会导致判断矩阵特征值的偏差，据此定义相容性指标。若矩阵A完全相容时，应有λmax=n，若不相容时，则λmax＞n，因此可应用λmax-n的关系来界定偏离相容性的程度。设相容性指标为C.I.，则有

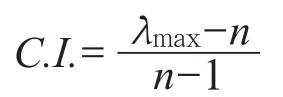
式中λmax——判断矩阵A的最大特征根。其算法如下。

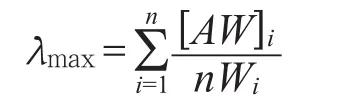
式中[AW]i——矩阵[AW]的第i个分量。

定义一致性指标CR为：

式中C.R.——随机性指标。

当一致时，C.I.=0；不一致时，一般有λmax＞n，因此C.I.＞0。故一般可根据C.I.＜0.1来判断。对于如何衡量C.I.可否被接受，Saaty构造了最不一致的情况，就是对不同n的比较矩阵中的元素，采取1/9，1/7，…，1，…，7，9随机取数的方式赋值，并且对不同n用了100～500个子样，计算其一致性指标，再求得其平均值，记为C.R.，结果如表4所示。

表4 平均随机性指标C.R.数值

若一致性指标CR＜0.10，则认为判断矩阵的一致性可以接受，权重向量W可以接受。

本例中，

4 计算综合重要度

计算综合重要度是层次分析法的最后一步，它决定了方案层的因素最终相对于项目总体的重要性。在计算递阶层次结构各层次对上一级要素的相对重要度之后，即可从最上层开始，自上而下的求出各层要素关于系统总体的综合重要度。

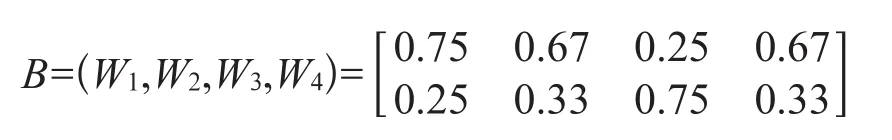
然后，用矩阵B乘以特征向量W，得到矩阵Wf，即

矩阵Wf表明，从最佳通信方案角度考虑，综合考虑了成本因素、实施难度、通信效果和后期维护几个因素后，McWill方案要略好于WLAN方案。

在应用层次分析法进行问题分析时，需要特别注意第二层（即准则层）参考因素的选择，本文中仅列举了4个参考因素，而在项目建设时的大型问题分析过程中，影响分析结果的参考因素可能多达数十个甚至上百个。面对如此多的参考因素，可以采用增加准则层子层的方法，将参考因素进行分组归类，再逐级分析影响方案的权重指标，最终计算出评选结果。由此可见，应用层次分析法时，如何建立完整、有效的参考因素库，如何精确的进行两两比较，给出准确的相对重要度分值，是应用层次分析法需要特别重视的两个关键因素。

层次分析法的应用，可以将难以量化的评价参量采用两两比较的方法，逐一进行比较，得到相对重要度参考值，再将两两比较结果综合计算，得出所有参量相对权重的量化指标，进而决定参评方案的优劣。层次分析法不仅可以应用于编组站建设项目中，在其他铁路领域的建设项目中都可以得到广泛应用，具有普遍的可推广性。

[1]沈建明.项目风险管理[M].北京：机械工业出版社，2003.

[2]殷焕武，王振林.项目管理导论[M].北京：机械工业出版社，2005.

[3] Gido Jack, James P.clements.成功的项目管理[M].张金成，译.北京：机械工业出版社，2006.