基于Adams与Matlab联合仿真的摆式列车动力学计算

周和超,梁寒冰

(同济大学 铁道与城市轨道交通研究院,上海200092)

摆式列车可以在不降低旅客乘坐舒适度的情况下以较高的速度通过曲线,这是既有线提速、增加铁路客运能力、提高铁路与其他交通工具竞争能力的一种有效办法。国外摆式列车的发展现已经进入成熟的运营阶段,我国的摆式列车研究工作也取得了不少的成果[1-3]。对于摆式列车这样的大型机电移动设备系统,从启动研发到最终产品定型,运用现有的先进计算技术和理论进行仿真模拟是主要的研究手段之一。Adams软件建立的虚拟模型能很好地反映实际的物理模型,其仿真结果也能很好地与实际物理模型的结果相吻合[4]。但是对于控制系统设计,Adams软件提供的控制工具箱只能处理一般的控制环节(比如PID控制),而Matlab/Simulink是大型控制系统设计软件,能够运行各种高级控制环节,如果将两者结合起来,充分发挥它们各自的优势,这将给那些复杂系统的研究提供一种新的途径。

1 摆式列车机电耦合动力学模型

运用多体动力学软件建立了摆式列车纵—横—垂向机电耦合动力学模型,考虑了列车系统中存在的轮轨几何接触关系非线性、轮轨蠕滑力非线性、车辆二系悬挂非线性等特点。整车动力学模型如图1所示,车体通过二系悬挂与摆枕连接,一对八字形吊杆(如图中AC,BD)将摆枕吊挂在构架上,机电作动器EF推动摆枕,使其带动车体一起倾摆运动。以摆枕和构架为例,其动力学运动方程为:

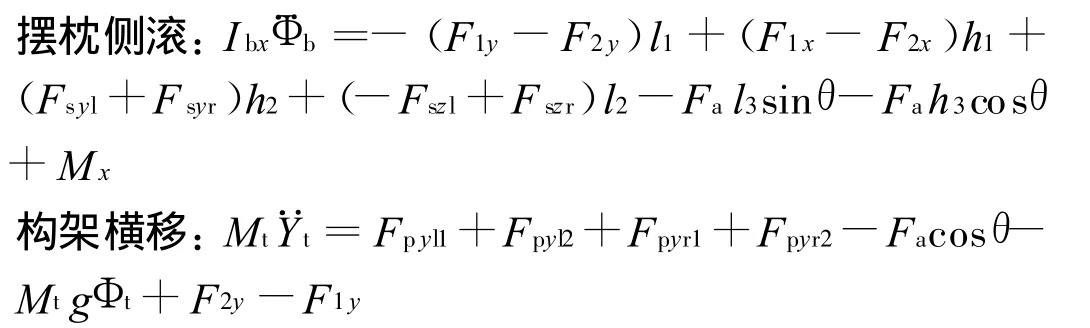
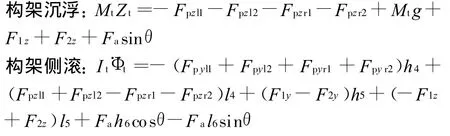
式中M,I分别代表质量、惯性矩;y,z,Φ代表横向、垂向位移及侧滚角。下标:i=1～2(1为导向轮对,2为后随轮对);p,s代表一系、二系;w,t,b代表轮对、构架及摆枕;r,l代表左右;h1,h2,h3分别为吊杆下铰点(C,D)、二系悬挂以及作动器上铰点(F)到摆枕质心的垂直距离;h4,h5,h6分别为一系悬挂、吊杆上铰点(A,B)以及作动器下铰点(e)到构架质心的垂直距离;l1为吊杆下铰点C,D间距离之半;l2,l3分别为二系悬挂和作动器上铰点(F)到摆枕质心的横向距离;l4,l5,l6分别为一系悬挂、吊杆上铰点(A,B)以及作动器下铰点(E)到构架质心的横向距离;Mx为抗侧滚力矩;F1,2为左右吊杆作用力;Fs为二系悬挂作用力;Fa为作动器作用力。至于车辆其他部件的动力学方程可参考文献[5],这里不用赘述。

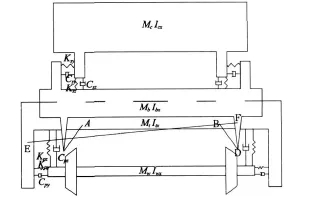
图1 整车动力学模型

2 Adams与Simulink联合仿真技术在摆式列车上的应用

Adams与Simulink联合仿真要经过以下的几个步骤[6]:

(1)在Adams与Simulink软件中分别建立虚拟模型以及控制系统

对于简单的模型可以利用Adams软件直接建模,对于复杂的模型可以借助一些CAD软件(如 UG、CATIA、PRO/E等)建模,然后将最终的模型导入到Adams环境中,最后给这个模型施加约束和作用力,建立的摆式列车模型如图2。

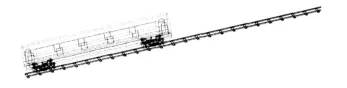
图2 摆式列车动力学模型

(2)定义Adams的输入和输出,并完成软件间的接口设置

Adams的输入输出是与Simulink设计的控制系统进行数据传递的接口,如图3所示。Adams的输入就相当于控制系统的输出,Adams的输出为控制系统的输入,从而形成一个闭环系统。

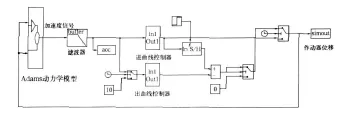
图3 摆式列车闭环控制系统

(3)仿真计算

对整个闭环系统进行仿真计算,根据结果进行参数优化处理,直至获得较满意的计算结果。

3 摆式列车动力学性能仿真研究

3.1 车辆蛇行运动稳定性计算

由于是非线性系统,采用数值仿真方法,在不同速度下,对车辆系统施加初始激励后让其在理想线路上运行,观察车辆各部件特别是转向架各轮对的自由运动情况。程序中通过极限环来判定非线性车辆系统的蛇行稳定性。这种方法的基本原理是当车辆系统受到一个初始激扰后,观察该系统各刚体的振动情况,用相平面来分析各刚体极限环的收敛和发散。如收敛,则车辆是稳定的;如发散,则车辆处于失稳状态;如极限环不收敛,也不发散,处于一种临界状态,此时车辆的运行速度称为车辆的蛇行运动临界速度vcr。

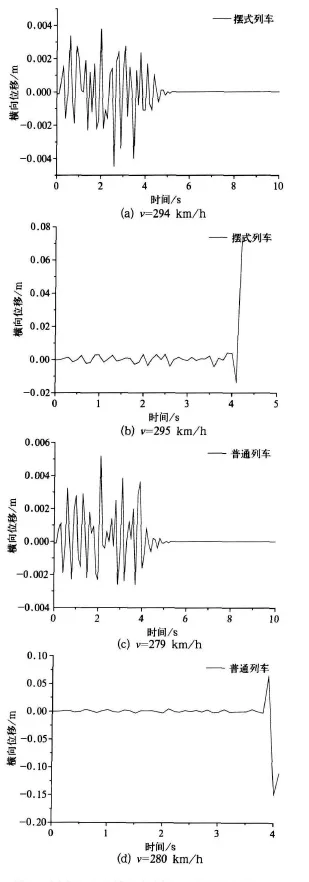
图4 摆式列车和客车临界速度模拟计算结果

从图4中可以看出,在运行速度为279 km/h,具有相同参数的普通客车轮对的横向运动是较快收敛的;在运行速度为280 km/h时,轮对的横向运动出现发散。因此可以认为在空车状态下,普通客车的临界速度在279 km/h左右。同理可以看出摆式列车的临界速度略高于普通客车,达到294 km/h左右。

3.2 车辆曲线通过性能计算

曲线通过性能主要包括安全性、磨耗和平稳性等指标。具体地有转向架各轮对的横向位移、冲角、横向作用力、脱轨系数、轮重减载率、磨耗功和曲线上运行平稳性等。选取以下工况进行仿真计算,并通过摆式列车和具有相同参数的普通列车之间的对比来对摆式列车的曲线通过性能进行深入的研究。

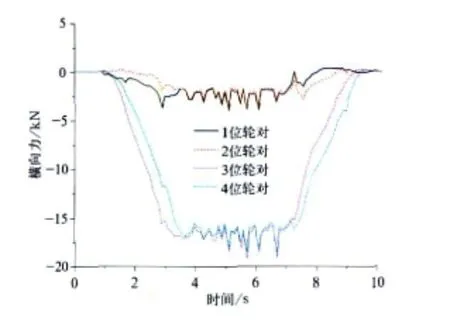
图5 摆式列车横向力

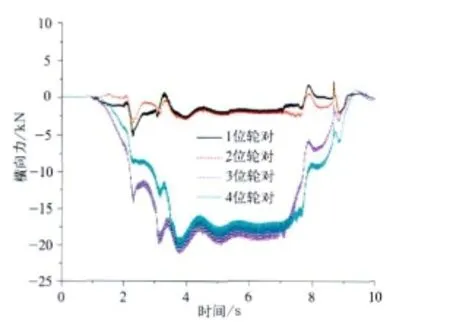
图6 普通列车横向力

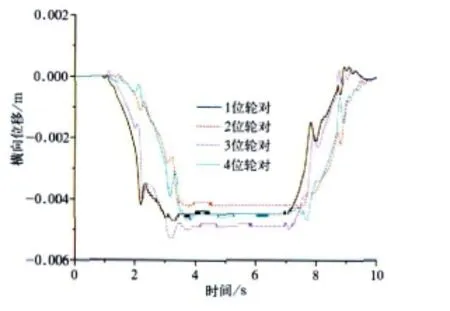
图7 摆式列车横向位移

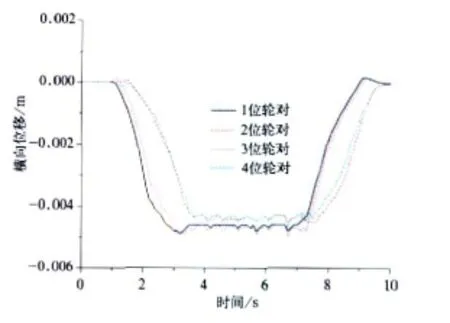
图8 普通列车横向位移

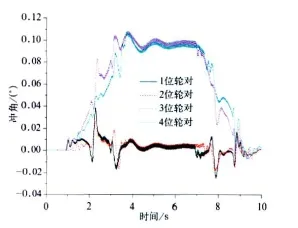
图9 摆式列车冲角

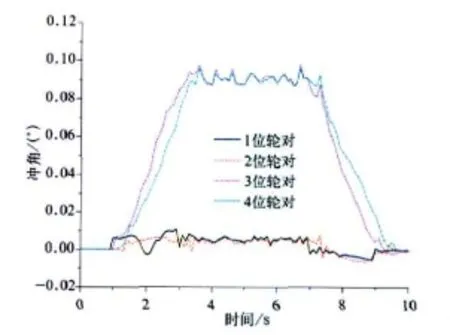
图10 普通列车冲角

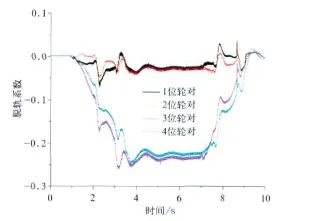
图11 摆式列车脱轨系数

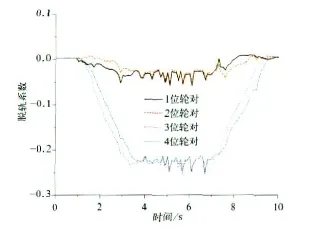
图12 普通列车脱轨系数

仿真线路:理想光滑曲线,曲线半径R=1 500 m,外轨超高h=30mm,初始直线Lt=45m,缓和曲线长度Ls=90 m,圆曲线长度Lc=180 m,缓和曲线长度Ls=90 m,直线Lt=45 m,曲线全长为450 m。曲线通过速度v=160 km/h。

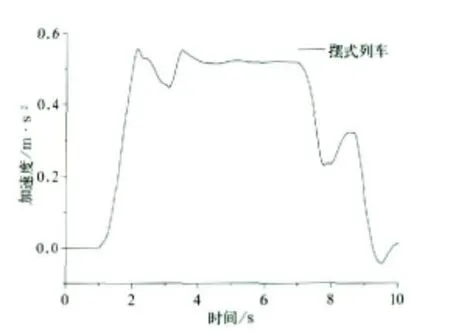
图13 摆式列车未平衡加速度

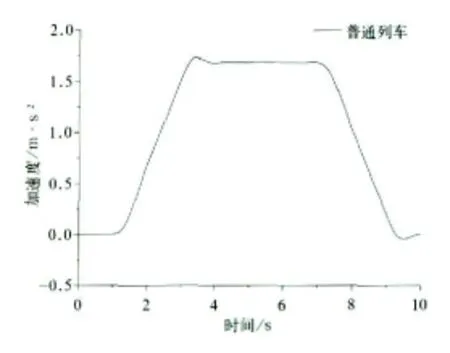
图14 普通列车未平衡加速度

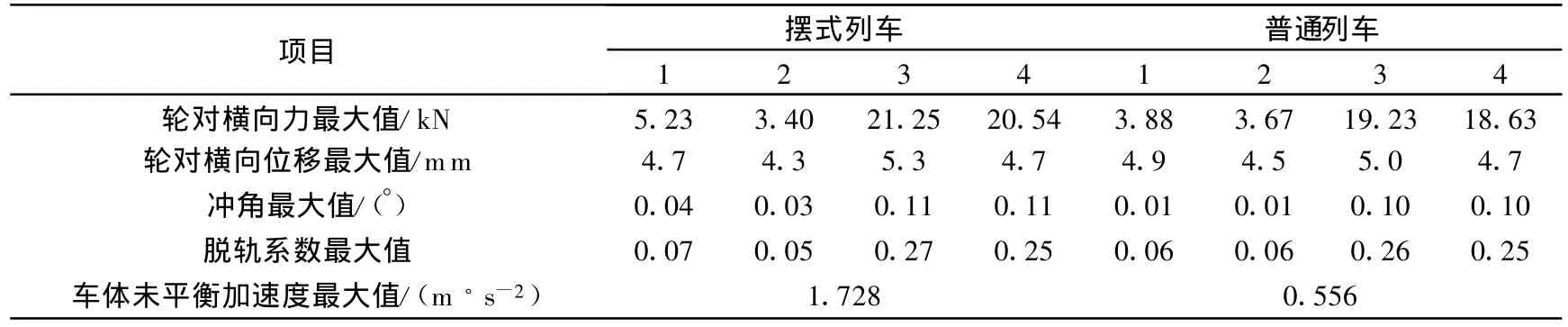
表1 曲线通过动力学性能比较

对照图5～图14以及表1可知,摆式列车通过曲线时,其动力学性能与普通列车相比差别不大。轮对横向力、横向位移、冲角以及脱轨系数有些车辆略大于普通车辆。其中轮对横向力和横向位移的最大值分别由19.23 kN 、5.0 mm增加 到21.25 kN 、5.3 mm,分别 提高了10.5%和6%。但由于摆式列车通过曲线时,机电作动器根据控制算法推动摆枕并带动车体一起倾摆,从而使车体未平衡加速度由1.728 m/s2下降到0.556 m/s2,降幅达67.8%,达到改善乘坐舒适度并提高曲线通过速度的目的。因此,摆式列车是在较小影响其动力学性能的前提下,明显改善旅客乘坐舒适度并能提高列车曲线通过速度。

5 结束语

本文利用Adams和Matlab/Simulink联合仿真技术对摆式列车机电耦合系统进行了动力学仿真分析,这也为那些高度复杂同时还需要进行控制设计的机械系统提供了一条新的研究途径。另外,根据此次的仿真分析可以看出摆式列车具有在较小影响其动力学性能的前提下,明显改善旅客乘坐舒适度并提高列车曲线通过速度的优势,具有很高的应用价值。

[1] 罗 仁,曾 京.摆式列车主动倾摆控制的数值仿真研究[J].铁道学报,2006,28(5):28-34.

[2] Pratt I.,Goodall R..Controlling the ride quality of the central portion of a high-speed railway vehicle.American Control Conference,Vol.1719-1723.

[3] Anderson E,Bahr H V and Nilstam N G.Allowing higher speeds on existing tracks-design consideration of the X2000 train for Swedish State Railways[J].Proceedings of the Institution of Mechanical Engineers(Part F,Journal of Rail and Rapid T ransit),1995,209(F2):93-104.

[4] 王成国.MSC.ADAMS/Rail基础教程[M].北京:科学出版社,2005.

[5] 王涛,张会明.基于ADAMS和M ATLAB的联合控制系统的仿真[J].机械工程与自动化,2005,44(3):79-81.

[6] 翟婉明.车辆—轨道耦合动力学(第2版)[M].北京:中国铁道出版社,2002.