基于最大似然的GPS转发式干扰信号估计方法

刘慧越,张爱勇,唐 斌

(北京5136信箱,北京100094)

0 引 言

GPS干扰从体制上可分为压制式干扰和欺骗式干扰。转发式干扰是欺骗式干扰的一种,其基本原理为:将干扰机接收到的GPS信号,经过一段时间延时、放大后直接发送出去。转发式信号幅度大于直视信号的幅度,GPS接收机将会跟踪干扰信号,从而产生错误的伪距。同其他干扰方式相比,转发式干扰在技术上比较容易实现,在战时将是对GPS最主要的干扰方式[1]。

鉴于转发式干扰的突出优点,美军将GPS抗转发式干扰技术列为重点展开研究。美国导航协会(ION)在2005年会上,将抗转发式干扰设立了相应的专题,定为机密级[3],对外是严格保密的。2006年,McDowell等申请了基于数字空域调零技术(digital spatial nulling)的抗转发式干扰系统的专利[4]。研制抗转发式干扰系统前提是必须正确地估计转发式干扰信号。

由于转发式干扰信号与多径信号相似性,将多径抑制技术思想应用于转发式干扰估计,利用相干积分累加计算的结果进行时域处理,估计结果用于后续的码跟踪环路,进行转发式干扰消除。常用的多径信号处理技术主要有窄相关技术和最大似然多径估计技术。缩短相关长度具有非常明显的优势,主要表现在噪声和多径干扰条件下,能有效地降低码跟踪误差[5]。通过窄相关技术,系统能够有效地提高抗多径能力和测距精度,但是,当多径数较多时,尤其面对人为的、具有较大幅度的转发式干扰时,窄相关技术则存在很大的困难。最大似然估计器(Maximum Likelihood Estimation,简记为MLE)通过估计多径信号的延迟和反射信号强度抑制多径,MLE多径估计技术以其优异的性能引起极大关注。提出的利用最大似然估计技术估计转发式干扰信号的新方法,首先建立GPS接收机对转发式干扰信号相干积分累加的数学模型,然后推导在有色噪声条件下转发式干扰信号的最大似然估计计算公式,实验证明了该算法的有效性。

1 GPS接收机中转发式干扰信号码的相干积分累加的数学模型

设aj(a0为直视信号幅度)为第j路转发式干扰信号幅度;τj(τ0为直视信号延迟)为第j路转发式干扰信号延迟;θj(θ0为直视信号相位)为第j路转发式干扰信号相位,输入到GPS接收机射频前端的L1频点C/A码信号可以表示为

式中:m为转发式干扰信号数;A(t)为调制信息;c(◦)表示C/A码;ω0为载波的标称频率;ωd为载波多普勒频移;n(t)为输入高斯白噪声。基于最大似然估计的转发式干扰估计的模型如图1所示。

图1 基于最大似然估计的转发式干扰估计模型

输入信号与来自载波跟踪环路的本地载波cos(ωrt+θ)相乘剥离载波信号后,同n路本地码做相干积分累加,各路的多径延迟估计分别为β0,β1,β2,…,βn。相干积分累加输出为

式中:Δω=ω0+ωd-ωr为载波跟踪残差;Δ θ=θj-θ为载波相位跟踪残差;Rc(◦)为码的自相关函数;w为通过积分累加器后的噪声;T为相干积分累加时间;C/A码信号调制信息周期为20 ms;T一般为1 ms;在积分累加时间内认为A(t)是不变的,设为1;为便于分析转发式干扰的影响,设载波环完全跟踪,则

式(2)表示为

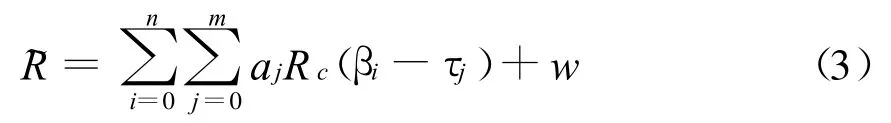
用矩阵形式表示为

式(4)即为所有接收信号码的相干积分累加输出的线性模型,其中

2 转发式干扰信号的最大似然估计

对式(4)中转发式干扰信号的估计,即为对线性模型中向量a的估计,当无噪声时,依据最小二乘估计理论,向量a的估计可以写成

如图1所示,噪声n通过相关器积分累加后,相当于一个低通的高斯过程,输出等价表示为

式中:hlpf(t)为积分累加器的脉冲响应;*表示卷积;wi(t)为单边功率谱N0,带宽为[-BW,BW]的高斯噪声,BW=1/T。第i路和第j路噪声的相关函数表示为

式中:

Δβij=βi-βj为噪声低通滤波后的自相关函数;当延迟τ=0时,设低通滤波后的噪声方差为

式中:σ2=N0BW,τ=0时,将式(9)代入到式(8)得

设

观测噪声w=[w0,w1,…,wn]的方差为Cw,则

影响观测噪声w的有两部分,一是单点噪声方差σ2;另一部分是协方差矩阵Pw。对于式(4),w～N(0,Cw),˜R～N(Ha,Cw),˜R是一个高斯过程,则˜R的概率密度函数为[6]

式中:det表示矩阵的行列式,则似然函数定义为

在有色高斯噪声的情况下,式(4)的线性模型的最大似然估计为等价于最小方差无偏估计量,并且达到Cramer-Rao下限,可以写为

3 GPS转发式干扰估计的仿真验证

实验中设直视信号幅值为1,不加入任何噪声,码相位延迟为0,任设直视信号和四个转发式干扰信号的幅值为a=(1,2.1,1.6,1.2,1.8)。码相位延迟τ=(0,0.2,0.6,0.9,1.2)。码相位延迟搜索范围β∈[0,1.5](与多径信号类似,若码相位延迟超过1.5个码片,将不会对码跟踪环路产生影响),搜索步长为0.1。

观测矩阵˜R的计算则利用式(2)进行。由式(9)知,低通滤波后的噪声的方差为σ2,又直视信号的幅值为1,则相应信噪比s/n为(以能量表示)

式中:T为相干积分累加时间。

从而由式(12)可求出噪声w的方差Cw,然后将噪声的均方根值代入式(2)中,即可求得新的观测矩阵˜R。将式(11)求得的Pw,式(5)求得的H,以及˜R代入最大似然估计式(15),得到的转发式干扰信号估计幅值比例和延迟如图2所示。

从图2中可以看出,载噪比为45 dB-Hz时,在相干积分累加时间T为1 ms时,转发式信号估计值在相应延迟点上得到估计,但在其它延迟点,由于噪声的作用,仍存在一些较小幅度的杂点,这必然会影响最终对转发式信号的判断。在相干积分累加时间达到10 ms时,转发式信号估计值得到较精确的估计,噪声得到有效抑制。

图2 最大似然转发式干扰估计

4 结 论

转发式干扰是卫星导航系统的主要干扰方式,精确地估计转发式干扰信号成为研制抗转发式干扰系统必须解决的问题。提出了一种新的基于最大似然估计的转发式干扰信号的估计技术,推导转发式干扰信号的最大似然估计计算公式。仿真实现表明:该方法可以在有色噪声条件下,对多个转发式信号进行较精确的估计。目前,对某型号抗干扰软件接收机中通过对接收机实际码延迟锁定环测试,鉴别器曲线锁定点近似位于零点,从而可有效地消除了转发式干扰信号和噪声对码跟踪环路的影响,保证了较高的伪距测量精度。

[1] 王妍洁,董绪荣.转发式GPS干扰仿真研究[J].全球定位系统,2004,29(6):16-18.

[2] 曹艳霞,田 斌.GPS转发干扰模式的研究[J].电子科技,2006(4):67-70.

[3] GOLDSTEIN.D.Repeater Jammer Study[EB/OJ].2005-11,http://www.ion.org/meetings/.

[4] McDowell,CHARLES E.GPS spoofer and repeater mitigation system using digital spatial nulling:United States,7250903[P].2006-04-17.

[5] 张 欣.扩频通信数字基带信号处理算法及其VLSI实现[M].北京:科学出版社,2004:226-227.

[6] 樊昌信,张甫翊,徐炳样,等.通信原理[M].北京:国防工业出版社,2001:19-20.