基于剪辑支持向量机的雷达目标识别方法*

冷家旭 黄惠明 龙 方

(北京跟踪与通信技术研究所 北京 100094)

1 引言

高分辨一维距离像(High Resolution Range Profiles,HRRP)是目标多散射中心在雷达径向距离上的一维分布图,它包含了目标沿距离向精细的几何结构特征,对目标分类识别十分有价值。目前,HRRP目标识别系统的关键技术主要集中在特征提取与选择、分类器设计两方面。其中,分类器设计作为识别系统中最具决定性的环节,近年来得到了广泛、深入的研究。在基于统计决策理论的众多分类方法中,支持向量机(Support Vector Machines,SVM)在解决小样本、非线性及高维模式识别问题时表现出明显的优势[1～2],并成功应用在雷达目标识别领域[3]。

相对于其他分类方法,SVM分类精度高、泛化能力强。在训练阶段,SVM依靠训练集内的一部分向量(即:支持向量,SV)在核函数定义的高维空间F中构建一个最大边界超平面。在测试阶段,判决输出前SVM需要将测试样本与每一个SV结合构成核函数。然而在HRRP目标识别中,经常会出现提取的训练样本特征在分类边界附近混迭的现象,使得SVM训练时产生的SV数目较大,影响识别速度,而且还会干扰SVM判决函数的准确性。同时,核函数参数与SVM惩罚因子的取值也直接影响着识别性能。因此,本文提出一种剪辑支持向量机(Edit Support Vector Machines,ESVM)分类方法—首先利用聚类算法从大量训练样本中选择最具代表性的训练样本,再通过循环剪辑法去除分类边界附近混迭的训练样本,然后以理想核函数矩阵为参考标准确定高斯核函数参数与SVM惩罚因子,最后进行SVM训练与测试。相比于传统SVM,剪辑SVM的分类面更明显,训练过程计算复杂度更低,分类精度更高。另外,本文还针对低信噪情况,在预处理中采用小波去噪提高回波信噪比,进而提高目标识别率。外场实测数据的计算仿真实验,也进一步验证了上述方法的可行性与有效性。

2 小波去噪

在实际的工作环境中,受各种因素的影响,雷达回波中包含目标信号以及各种噪声信号,具有非平稳的特性。传统的Fourier变换对平稳信号有较好的分析能力,而对非平稳信号,由于存在保护信号局部特征和抑制噪声之间的矛盾,无法得到理想效果。小波变换则具有多分辨分析的特性和良好的时频局部化分析能力,能够很好的兼顾去噪和保护突变信号,有效抑制噪声[4]。因此,在目标识别前本文首先对受高斯加性噪声污染的HRRP进行小波变换,获得多层次小波分解系数,再利用自适应阈值对高频系数进行量化处理,最后进行反变换获得降噪后的HRRP。

在实际应用中,采用小波阈值降噪主要需要考虑四方面的内容:小波母函数的选择、信号分解层数的选择、门限阈值的确定以及阈值处理函数的选择。结合HRRP的非平稳、不连续特性,考虑降噪效果以及计算复杂度问题,本文使用sym8小波基函数,分解层数为5层,采用试探法无偏风险准则确定门限阈值,并使用硬阈值处理函数对小波分解系数进行量化处理。图 1给出了某型飞机实测H RRP在信噪比5dB时利用小波阈值去噪处理后的结果对比。去噪前H RRP与原始 HRRP的相关系数为0.7595,均方误差为0.004。去噪后HRRP与原始HRRP的相关系数为0.9440,均方误差为2.1191×10-4。可见,小波去噪能够较好的保留原始信号的有用信息,消除噪声。

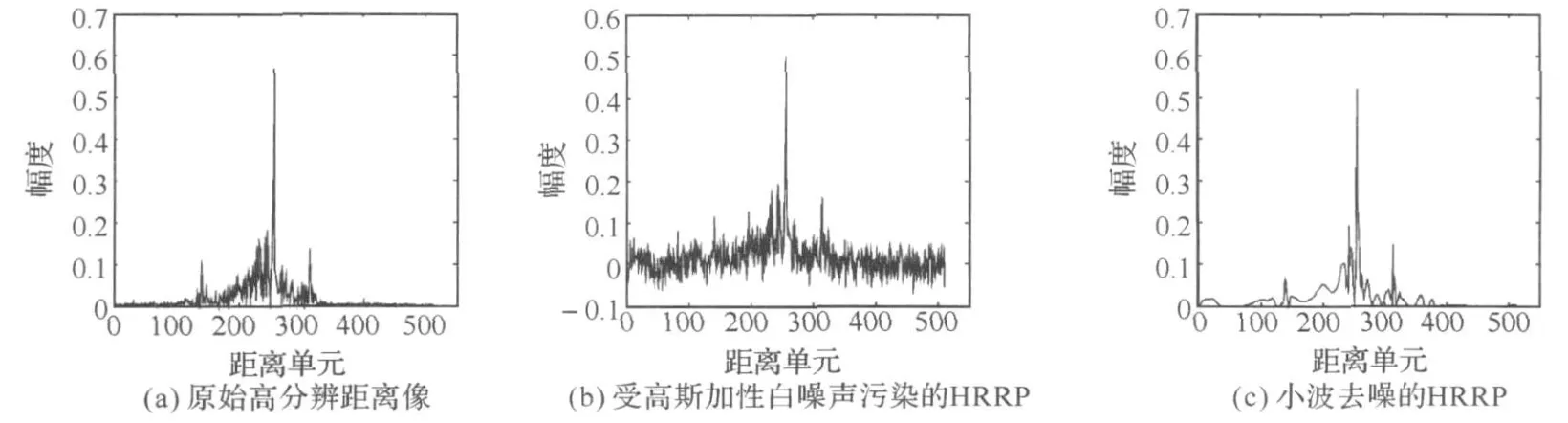
图1 小波去噪前后HRRP成像效果对比

3 剪辑SVM算法

3.1 SVM原理

SVM的主要思想是使用核函数将观测样本从输入空间映射到高维的特征空间,并在这个空间构造最优分类超平面。

其中,x为待分类样本,SV为支持向量集,b*为分类阈值。

对于线性不可分问题,可引入函数松弛因子ξi,求以下广义最优分类超平面问题。类似上述推导,可得线性不可分问题的广义最优分类判决函数为

对于非线性可分问题,超平面的分类能力有限,为此SVM 引入非线性映射 φ(x):Rd→E,将数据映射到更高维特征空间,从而能够线性可分。根据Mercer条件,用内积运算代替原空间最优判别函数的点积运算,可以得到新的特征空间中的最优判决函数

而对于L(L＞2)多类问题,本文使用“一对多”的方式,将其转化为L-1个两类问题。

3.2 SVM参数选取

在解决非线性可分问题时,SVM引入核函数,把低维空间中线性不可分问题转化为高维空间中的线性可分问题,但是由于核函数类型及参数选取的局限性,往往在映射后的高维空间也无法完全实现线性可分。因此SVM又引入了惩罚因子Cs vm,将问题转化为求解高维空间的广义最优分类超平面。文献[5]给出样本集X(M)线性可分的充分条件是Hess矩阵G满秩(其中:Gij=yiyjKij,Kij=K(xi◦xj)=〈φ(xi)◦φ(xj)〉为核矩阵)。并说明了在处理训练数据非线性可分情况时,引入惩罚因子Csvm相对于在原有的Hess矩阵对角线中增加一个常数1/Cs vm(即:Gc=G+(1/Csvm)I),使其满秩,即使得训练样本在核空间中变得线性可分。

Hess矩阵相似度S的值越大说明Gc越接近理想情况,可分性越好。本文使用高斯型核函数,因此只需确定σ和Csvm两个参数。图2(a)为Csvm=∞时不同高斯核参数σ下S变化情况,使用数据是3类目标H RRP实测数据的频谱幅度经过线性判决分析(LDA)获得的特征。S最大时对应的σ*即为最佳映射核参数,本实验中σ*=0.8400。不难计算出σ*对应的核矩阵非满秩,因此还需确定Csvm。图2(b)为σ*=0.8400时不同惩罚因子Csvm下S变化情况。可见,S随的增加而增加,并最终趋于平稳。但是的取值并非使S越大越好,过大时SVM训练过程将变得非常耗时;过小时Gc趋向于单位阵,将导致过度拟和。因此需在S与训练时耗之间折衷选择一个合适的,如本实验中可以选择=100。

图2 高斯核参数与SVM惩罚因子对样本线性可分性的影响

3.3 剪辑SVM

从式(5)不难看出,由于引入了计算复杂度与样本个数有关的核函数,SVM仅适用于小训练样本情况。但是小数目的训练样本无法保证能够完好的表征该类目标的分布特征。另外,SVM判决函数运算复杂度取决于支持向量的个数,对于小样本问题,支持向量的个数总是远小于样本数目,分类决策时的计算代价无需过多考虑。然而在训练阶段,分类面附近混迭的训练样本会增加支持向量的个数与计算复杂度,并影响SVM判决函数,进而影响识别性能。针对上述问题,本文提出一种新的SVM学习方法—剪辑SVM(ESVM)。

对于小样本表征目标分布问题,ESVM对每类目标的大量训练样本进行聚类,以聚类中心为ESVM所使用的训练样本。对于分类面混迭问题,ESVM通过循环剪辑最近邻法[6]清理类间边界,去掉类别混杂的样本,使类边界更清晰。对于参数取值问题,ESVM采用基于矩阵相似度的选优方法。

设X(N)={xi,yi}(i=1,2,…,N)为原始训练样本集,xi为样本特征,yi={1,2,…,C}为类别标记,C为目标类别数,N为训练样本数目。ESVM训练算法如下:

1)对各类目标样本分别进行聚类(本文使用k均值聚类算法),由M个聚类中心X(M)={xk,yk},(k=1,2,…,M)组成新训练样本集;

2)将样本集 X(M)随机地划分为s个子集:X(M)={X1,X2,…,Xs}(s≥3),并保证每个子集内均包含C类的训练样本;

3)用最近邻法,以 X(p+1)mods为参照集,对Xp中的样本进行分类,其中p=1,2,…,s;

4)去掉在3)中被错分类的样本,用所留下的样本构成新的样本集X(ME);

5)如果经过q次迭代后再没有样本被剪辑掉则转到6);否则转到2);

6)对于最终训练样本集X(ME),利用3.2节的方法确定高斯核参数σ与SVM惩罚因子Csvm;

7)利用 X(ME)与6)中求得的参数 σ、Csvm,训练SVM分类器。

如图3(a)所示,3类目标HRRP实测数据的频谱幅度经过线性判决分析(LDA)获得的特征分布图(2维),每类目标有6000个样本。图3(b)为经过k均值聚类得到的聚类中心分布图,每类目标有500个聚类中心。可以看出,经过聚类,数目较小的聚类中心样本集合能够很好的表征原始样本的分布情况。图3(c)为经过循环剪辑最近邻获得的样本分布图,不难发现,经过循环剪辑,原始混迭的分界变得清晰。图3(b)与图3(c)中的黑色实线表示由图中特征训练SVM得到的分界面,黑色空心点为相应的支持向量。表1列出了聚类后使用ESVM与SVM进行训练的支持向量个数及训练时耗。可见,ESVM无论在训练时间还是判决函数准确度等方面均优于传统SVM。

表1 ESVM与SVM训练性能与时耗比较

图3 聚类与剪辑处理对训练样本分布情况及SVM训练结果的影响

4 分类实验

为了检验上述方法的有效性,本文使用雷达实测飞机数据进行了仿真识别。该数据是取自国内某研究所宽带实验雷达的ISAR测量飞机数据,试验飞机有三种(T1,T2,T3),均为喷气式飞机。本文以5度姿态角间隔为一个角域单元,取相邻3个(目标近似径向飞行时为2个)角域单元内的样本进行训练生成36个模板库,每类目标每个模板库内包含6000个训练样本。测试样本取自其它段数据。

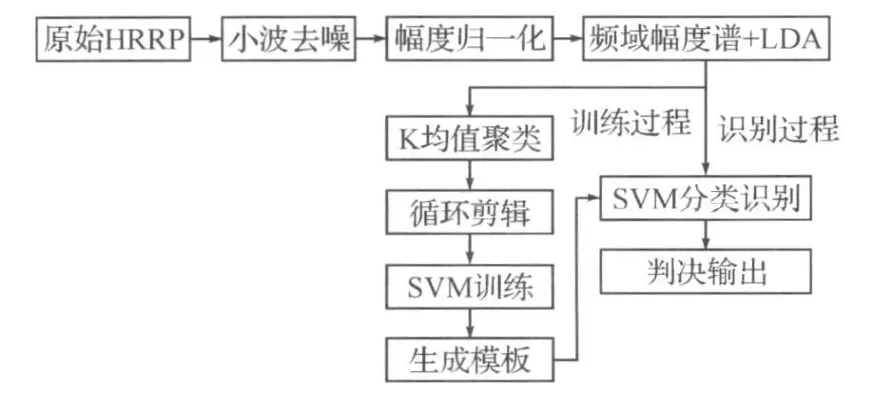
图4 仿真算法流程

为克服HRRP的平移敏感性并有效压缩特征维数,本文采用基于频谱幅度特征的线性判别分析算法(LDA)提取特征。具体识别流程如图4所示。其中:小波去噪使用sym8小波基函数,分解层数为5,使用试探法无偏风险准则确定门限阈值,并采用硬阈值处理函数;K均值聚类的聚类中心数为500。

图5 小波去噪对ESVM识别性能的影响

图5比较了在不同信噪比情况下小波去噪对目标识别率的影响,分类器采用ESVM。从图中可以看出,在低信噪比(SNR＜10dB)情况下,利用小波去噪可以有效抑制噪声,显著提高识别性能。但在较高信噪比情况下,小波去噪后的目标识别率反而有所降低。这是由于目标回波有用信号的能量主要集中在低频区,而噪声能量遍布整个频谱,在低信噪比情况下噪声能量较强,通过对高频系数进行自适应阈值处理可有效去除回波的高频噪声分量,提高回波信噪比;而在高信噪比情况下噪声能量相对较弱,此时对高频系数进行处理反而会去除有用信号的部分高频细节信息,引起信号失真,进而降低识别性能。因此在实际应用中,可以先估计目标H RRP的信噪比,低于某设定门限时才进行小波去噪预处理,高于门限的直接进行分类识别。

图6给出了未去噪与小波去噪后,ESVM、SVM、1NN三种分类器的识别率随信噪比的变化情况。实验中,1NN使用原始训练样本进行训练,ESVM和SVM使用聚类后的类心样本进行训练。不同于SVM,ESVM还进行了循环剪辑处理。由图中数据可以看出,未进行去噪处理时ESVM的识别性能明显优于SVM、1NN,这是由于ESVM通过剪辑处理使分类面更清晰,降低了最优分类面的计算难度,也减少了分类面附近混迭的样本点对SVM判决函数的干扰,因此其性能优于传统SVM与1NN分类器。同时还需要看到,小波去噪后三种分类器的性能差别变小,特别是低信噪情况下,这说明小波去噪对ESVM识别性能的提高幅度低于传统SVM和1NN,即:ESVM具有相对较强的噪声鲁棒性。实际上,这也是剪辑处理的作用结果,通过剪辑去除掉分类面混迭的样本,使类间距离更大,提高了最优分类面的计算精度,进而增强了分类器的推广能力。

5 结语

SVM分类器具有性能出色、结构简单、泛化能力强等优点,在解决小样本、非线性及高维模式识别问题中表现出明显的优势。但当出现训练样本存在数目过大、分界面混迭等问题时SVM的训练时耗、识别性能都受到影响。据此,本文提出一种剪辑SVM分类器—训练阶段通过聚类压缩样本数目,利用循环剪辑使边界清晰,并采用基于Hess矩阵相似度优选参数法选择合适的核参数与惩罚因子,进而降低SVM训练难度、提高分类精度;识别阶段又利用小波去噪提高低信噪比情况下的识别性能。基于实测数据的实验结果表明,本文方法识别性能优于传统SVM与最近邻分类器,而且训练时耗也明显少于传统SVM,是一种有效可行的H RRP目标分类方法。

[1]Vapnik N.The Nature of Statistical Learning Theory[M].New York:Springer Verlag,1995:1～188

[2]Schwenker,Hierarchical F.Support Vector Machines for Multi-class Pattern Recognition[C]//the Fourth International Conference on Knowledge-Based Intelligent Engineering Systems and Allied technologies,Brihton,UK,2000

[3]孟继成,杨万麟.基于核函数的雷达一维距离像目标识别[J].电子与信息学报,2005,27(3):462～466

[4]Donoho D L.Denoising by soft-thresholding[J].IEEE Trans on Information Theory,1995,41(3):613～627

[5]郭雷,肖怀铁,付强.目标识别中SVM 线性可分性研究[J].电子与信息学报,2009,31(3):570～573

[6]孙即祥.现代模式识别[M].长沙:国防科技大学出版社,2002