机床传动链测试系统及滚齿机精化实用技术

郑 永 郑方燕 高忠华 陈自然 董 淳

（①合肥工业大学仪器科学与光电工程学院，安徽 合肥 230009；②重庆理工大学机械检测技术与装备教育部工程研究中心，重庆 400054）

FMT［1-3］系统是“全微机化传动误差检测分析系统”的简称，在原有计数法测量传动误差基础上开创采用了新式的脉冲细分方法，使测量精度得到提高。它摒弃了传统仪器中复杂的电器箱部分，只保留传感器部分，所有的信息处理全由计算机完成，使得全套系统因结构大大简化而成本降低、故障率低、环节误差少，同时测量精度高、分析功能强、操作简便。FMT 系统在国防和机床、齿轮行业应用效果突出，于1995 年获国家教委科技进步二等奖，1996 年被国家科委列为“国家级科技成果重点推广计划项目”。由于FMT 系统自身性能优越，测试可靠，在陕西第二机床厂等十多个国内主要齿轮和齿轮机床生产厂家得到应用，深受用户厂家的欢迎。笔者采用基于谐波分析的修正技术对低精度机床进行精化改造，将普通滚齿机精化成为高精度蜗轮加工机床，实现了高精度蜗轮加工的低成本化。

1 机床传动链误差谐波分析法

在有关电信号处理的理论体系中，除了电磁波等少数领域涉及的物理量外，大多为时域或频域，自变量为时间，即可认为电信号的变化与空间无关，只与时间有关。常见的表达式为

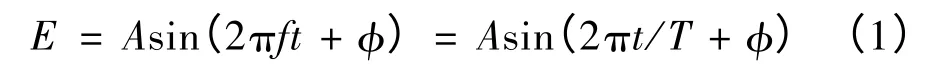
式中，T 为信号交变的时间周期。

正如电信号总是与时间相关，机械信息则总是与空间相关。典型的例子就是旋转机械运动，以一个圆周W=360°为空间周期，其函数表达式为

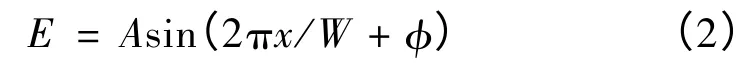
即信息是随空间位置x 的变化周期性地改变。只是由于机械一旦运动起来，同时也就成为时间的函数，而人们又习惯于时域的思维方式和成熟的理论体系，因此较少有人采用式（2）反映的“空间域”或空域的概念去分析问题。但是针对一些具体问题，采用空域分析将更为方便［4］。

在机床的齿轮传动链中，每个齿轮的转速不同，均有各自的轴频（每转变化一次）误差和齿频（每齿变化一次）误差，所有的误差叠加在一起，构成了机床总的传动误差。

传动链中每个回转传动件传动误差的主要部分，均为其转角的正弦（或余弦）函数，如式（2）。研究表明，对于这种以式（2）反映的数学模型为其变化规律的误差信息，采用等空间间隔采样的测试效果，要远远好于按等时间间隔采样的测试效果。只要在机床传动链的两端各安装一个按空间均匀分度的栅式传感器（如光栅），以其中一个为基准，每到一个脉冲（每过一段同样的空间间隔）进行一次采样，由此得到的一条实测曲线。显然这是一条空域曲线，它的横坐标是空间间隔，与时间、运动速度无关。

由于机械转动的速度很难保持恒定，因此基于时域（等时间间隔）的数据采集很难保证空间数据的整周期性。但空域即等空间间隔的数据采集则容易做到，通常取旋转一周的采样数据点为N=2n，其中n 为整数，最有利于FFT。N 取多少取决于研究者欲观测的最高谐波次数m，按采样定理，N≥2m。据此测得空域离散数据x（i）（i=1，2，…，N-1），x（i）的具体物理含义可以是转矩、转速、加速度、传动误差等。对其进行与FFT 相似的空间傅里叶变换（SFFT），则有：

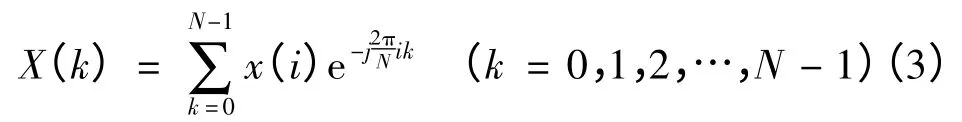
式中：X（k）为序号k 对应的谐波分量幅值；k 为频谱中位置序号，即谐波次数。空域FFT 和时域FFT 的算法相似，但物理意义和谱位置计算不同。空域曲线表征了被测动态参数随角位移变化的情况，其傅里叶结果表征了该参数随空间频率的分布情况。

传动链中每个传动件传动误差的传递，符合卡拉希尼柯夫误差传递理论，该理论运用在机床齿轮传动中，可归结为误差按传动比传递［5］。可以表达为

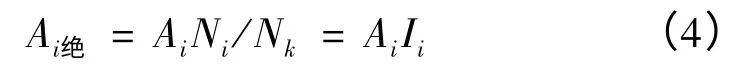
式中：Ai绝为i 传动件绝对传动误差模值；Nk为k 传动件转速；Ni为i 传动件转速；Ai为传动误差曲线中Ni/Nk次谐波对应幅值；Ii为i 传动件对于k 的传动比。

因此，对传动误差曲线进行SFFT，就能获取传动链中任一环节的误差，然后根据这一误差进行修正。

2 传动误差测量及分析

机床传动链传动误差动态测量采用FMT 系统进行测量。本项目中采用德国海德汉886 型光栅（36000 线，±1″精度）作为低速端（工作台）传感器，高速端（刀杆轴）采用长春宇衡ZKT -58A 型传感器。利用FMT 系统对Y3180H 滚齿机进行精化。现场测试如图1。

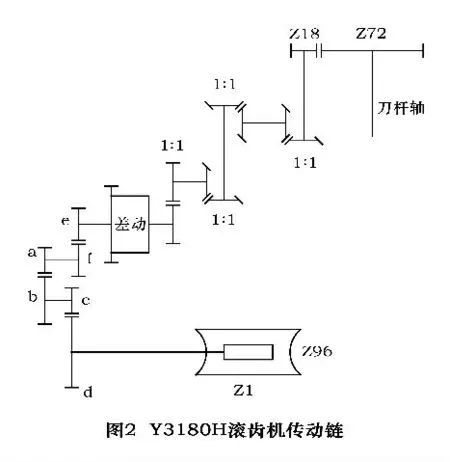
图2 是Y3180H 滚齿机的传动链图。该机床最大加工直径为800 mm，最大模数为10，加工等级6 级。将滚齿机的传动链调节成（通过调节分齿挂轮组a、b、c、d、e、f 来实现）刀杆和工作台转速比为100:1，也就是加工蜗轮头数为1，齿数为100 的工作状态。

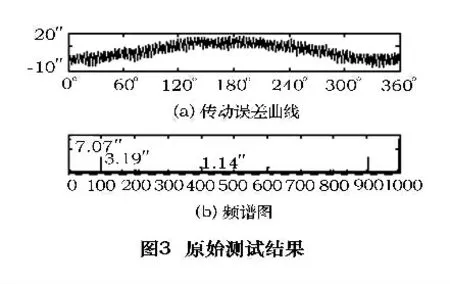
安装调整好传感器后，启动滚齿机，使其处于正常工作状态，这时开启FMT 系统进行测试。测试的原始误差曲线和频谱如图3 所示。

由图3 可知该机床传动误差为24.96″，累积误差为15.92″，周期误差为9.16″，其误差主要的谐波频次为1、96、400，幅值分别为7.07″，3.19″，1.14″。结合图2，经过分析可以得出1 次谐波是由于工作台蜗轮误差引入；96 次谐波是由工作台蜗杆误差引入；因为传动比为100，而锥齿轮转速刚好是刀杆轴的4 倍，所以400 次谐波是由锥齿轮误差引入的。因此机床的三个主要误差环节是工作台蜗轮、工作台蜗杆和锥齿轮。传动链中的各个传动环节误差，按照传动误差传递规律、依照传动比分别折算到传动链末端（工作台），最后合成了图3 的误差曲线。工作台蜗轮、工作台蜗杆都处于传动链的尾端，其折算系数（传动比）小，特别是蜗轮，是按照1:1 进行误差传递的。锥齿轮误差主要是由于其自身的制造误差以及热处理工艺等引起的变形带来的，尽管其处于传动链的前端，但是折算后的误差依然很大。下面即着手对这3 个主要的误差源进行精化修正。

3 对锥齿轮和蜗杆误差的修正

对锥齿轮和蜗杆误差的修正方法类似，就是附加一个人造已知误差与原有误差进行合成，合成后的误差为零。结合到对锥齿轮和蜗杆误差的修正则是在它们相连的传动链环节中加入偏心人造误差，误差值与它们自身产生的误差值相同，然后调整相位，最终使人造误差和原有误差相互抵消，从而起到对锥齿轮和蜗杆误差的修正。

首先是对锥齿轮误差的修正。由图3b 可知400次谐波的幅值为1.14″，因此锥齿轮自身带来的绝对误差幅值由式（4）可得：

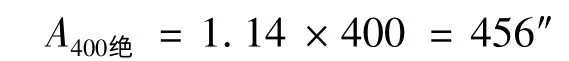
因此需要将差动包前级的e 轮增加一个偏心量e1，使其产生的误差刚好是456″。假设e 轮分度圆半径为d，那么e1计算公式为

式中的e1单位同d 的单位。将齿轮e 的分度圆直径代入得出e1=159 μm，重新加工一个齿轮e，并将中心孔做一个159 μm 的偏心。

安装上偏心齿轮e，然后调整其安装角度，当400次谐波幅值最小时即为最佳位置，这时，测出的传动误差曲线和频谱图如图4 所示。

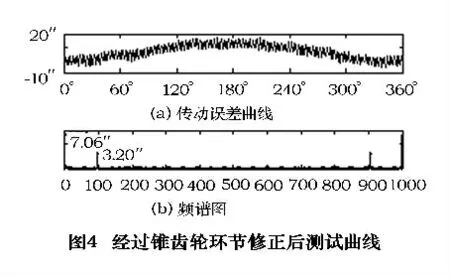
对比这两次测量曲线的频谱图可以得知，经过锥齿轮误差修正后，锥齿轮的误差基本上消失，在频谱上主要有1 次和96 次谐波误差。

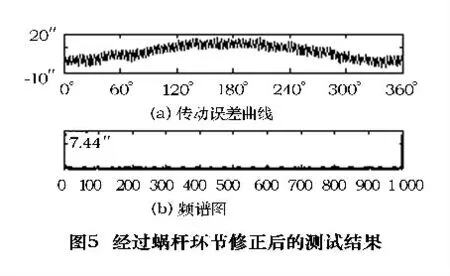
下面将对蜗杆环节误差进行修正，方法类似上面对锥齿轮误差的修正。在图2 所示的d 齿轮加入一个偏心量，计算方法同上。有图4b 可知蜗杆误差分量（即96 次谐波）的幅值为3.20″，首先计算A96绝=3.20×96=307″，然后将其和d 齿轮的分度圆直径代入式（5），得到d 齿轮的偏心量e2=149 μm，将重新加工好的带e2偏心的齿轮d 装好，然后调节安装角度，当96次谐波幅值最小时即为最佳位置。这时，测出的传动误差曲线和频谱图如图5 所示。

从图5b 可以看出，经过锥齿轮和蜗杆误差修正后，只剩下传动误差曲线中1 次谐波误差特别突出，而其它高频误差幅值比较小。

图6 带偏心的e 和d 齿轮后的实物图，图中齿轮中间的接盘是为了调节安装角度的装置。

4 对蜗轮环节的修正

对于蜗轮的修正要比前面两个的修正过程要复杂一些，因为蜗轮引入的误差不是单纯的正弦规律，即使是正弦规律，由于它是传动链的末端，无法使用加偏心的方法进行修正。蜗轮引入的误差比较复杂，这是由于蜗轮加工工艺等原因引入的，因此对于这种复杂的误差必须采用另外的方法进行修正。

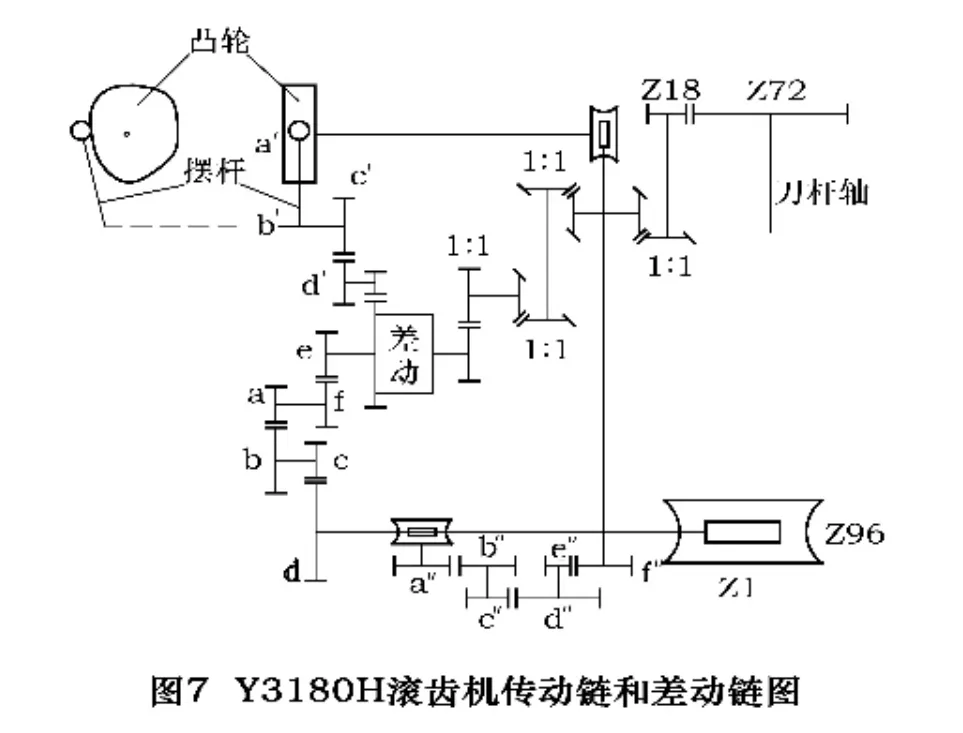
滚齿机加工斜齿轮时需要两个运动，一个是产生渐开线的展成运动，这个运动与加工直齿轮时相同，即滚刀旋转和工件旋转的运动；另一个是产生螺旋线的成形运动，它也可分解为两部分，即刀架的直线运动和工件的附加转动。由于形成渐开线要求工件转动，差动传动链也要求工件附加转动，但是这两个运动如果同时传给工件，会使工件发生干涉。因此需要一个运动合成装置，差动装置是根据行星齿轮的原理来设计的，它的作用是将两个输入合成一个输出。因此，可以利用差动装置来对蜗轮的误差进行修正，让差动链的附加运动产生的误差刚好和蜗轮产生的误差相互抵消，从而达到修正蜗轮误差的目的。滚齿机蜗轮修正原理图如图7 所示。

如图7 所示，a′～d′4 个齿轮是差动挂轮组。此处a′换成凸轮，b′上安装摆杆，c′、d′作为放大比调整齿轮（这里采用1：1）。用弹簧来保证摆杆与凸轮单向贴紧，凸轮半径的变化将通过摆杆使b′轴增加一个回转运动，该运动通过c′，d′，差动机构将会给工作台带来一个附加的运动。a″～f″为进给挂轮组，为了达到修正蜗轮误差的目的，一定要使凸轮和工作台同步转动，也就是a′轴与工作台的传动比为1:1，才能保证凸轮正好能够修复蜗轮一周的误差。

接着就是确定凸轮半径变化方向和误差曲线的关系。经过实测，凸轮半径增加时，误差曲线会向下偏移，也就是说将原始误差曲线做成凸轮半径正变化，这时附加运动产生的误差曲线应和原始误差曲线相反，也就是起到了修正误差的目的。

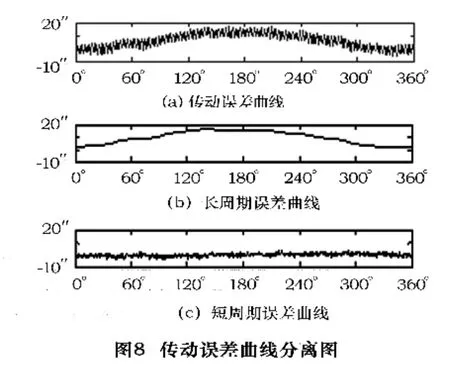
下面工作重点就是对图5a 误差曲线进行分离［6-8］并提取出蜗轮误差曲线，然后根据这一误差曲线设计一个合适的差动链补偿系统将其修正。对曲线进行误差分离，分离成两条曲线，如图8 所示。图8b是此误差曲线对应的长周期（累积误差）曲线，图8c是对应的短周期曲线。图8b 中的曲线代表蜗轮运动一周的误差变化，利用这条曲线制作一个凸轮，凸轮一周的半径变化规律与曲线变化规律一致。让这个凸轮和机床的蜗轮同步转动，则凸轮引起的附加运动与图8b 中的曲线代表的误差相抵消。

为了将图8b 中曲线各点数据变成凸轮半径的变化，需要计算误差曲线上1″误差对应摆杆末端偏移的距离（凸轮半径的变化量），也就是折算系数。设摆杆长度为R摆，b′轴对工作台的传动比为I摆，那么折算系数k 为

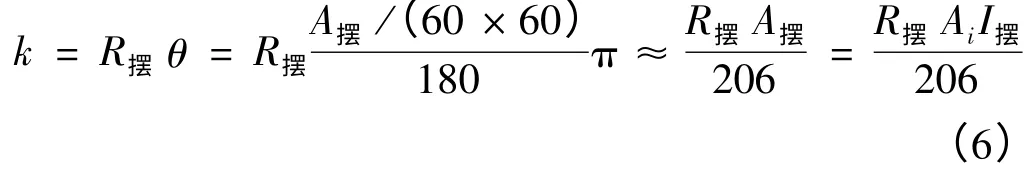
由式（6）可以看出，为了使计算方便，设计摆杆R摆=206 mm 将会简化公式，当Ai=1″时，折算系数k=I摆。由图7 中的传动链可以得出I摆=288，因此折算系数k=288，单位为mm/（″）。算出折算系数后，就可以根据图7b 中的曲线数据计算凸轮的半径偏移量。设曲线中第i 个点的数值为Di（单位为（″）），那个i 点对应的半径Δri为

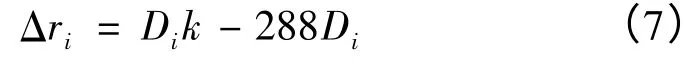
设r 为凸轮没有半径变化时的半径（也就是凸轮初始时是个圆），凸轮第i 点的半径r凸i（单位为mm）为

凸轮半径数据计算出来后，要对得出的数据进行适当的处理，使其可以在线切割机床中加工出来。AutoCAD 中可以使用命令窗口输入命令，由于传动误差曲线每周的采样点数为1000，每个点对应的角度值为360/1000=0.36°，因此设计一个等差数列，从0°开始，依次增加0.36°，一直增加到360°，第i 个角度值对应的半径为r凸i，然后以极坐标命令形式画出凸轮。将画好的图纸导出成线切割可以辨识的文件格式，导入线切割机床主控系统后就可以加工凸轮了。安装后的凸轮如图9 所示。

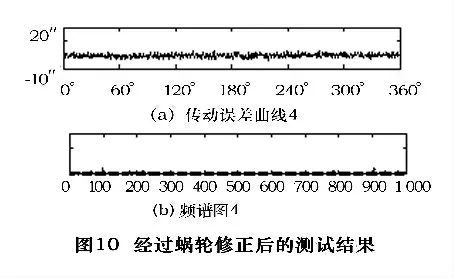
凸轮安装完后测试，得到最终的传动误差曲线及频谱如图10 所示。测试数据为：传动误差7.55″，周期误差4.23″，累积误差3.41″。

5 结果分析与总结

国标GB10089 -88 中蜗轮副传动切向综合误差ΔF′ic（可理解为传动误差），传动一齿切向综合误差Δf′ic（可理解为周期误差），可根据国标中给出的公式和数据表进行计算得出。对照这两项指标，以精度较低的等级为准，表明本机床已从出厂规定的6 级加工精度，提高到1 级或2 级精度。其效果是非常明显的。而实际加工精度还要取决于刀具、装夹和操作等因素。

此外还可看出，经过三次误差修正后，传动误差曲线基本上是一条比较直的曲线，基于谐波分析修正技术行之有效。下一步采取两条途径可以进一步改进测量效果，一条是增大采样点数，使传动误差曲线更能反映真实的误差情况；另一条是采用新的方法加工凸轮，使凸轮的精度进一步提高。计划采用时栅空心转台（提高凸轮的分度精度）和带钼丝直径补偿系统的线切割机床加工凸轮。这个新式的线切割机床将另文介绍。第三就是在轴承、机床刚性等环节再下功夫，有可能将高频误差进一步缩小。

［1］彭东林，谭为民，刘小康，等.机床传动误差测量中的空域法分析［J］.农业机械学报，2003.34（5）：123 -125.

［2］彭东林，张光辉，郭松涛，等.传动误差检测系统FMT［J］.制造技术与机床，1996（5）：20 -22.

［3］彭东林，张光辉，郭晓东，等.传动误差测量数学模型及FMT 系统实践［J］.制造技术与机床，1996（6）：13 -15.

［4］彭东林.时栅位移传感器与新型机床动态检测系统［M］.北京.科学出版社，2010.

［5］和子康.机床传动精度测量和提高［M］.北京.中国计量出版社，1987.

［6］洪迈生，蔡萍.多步法误差分离技术的比较分析［J］.上海交通大学学报，2004，38（6）：877 -881.

［7］曹麟祥，谢会崇，王红，等.全谐波误差分离技术［J］.宇航计测技术，1992（6）：1 -3.

［8］任克强，刘晖.微机控制系统的数字滤波算法［J］.现代电子技术，2003（3）：15 -18.