采用 EXCEL试算法进行混凝土徐变函数的拟合
2010-04-23李晓勇
王 杉,李晓勇
(中国水电顾问集团成都勘测设计研究院,四川 成都 610072)
1 前 言
混凝土在正常荷载持续作用下,其变形随时间不断增加,这种现象称为徐变。徐变变形比瞬时弹性变形大 1~3倍,因此,徐变在结构计算中是不可忽略的一个重要因素。徐变对结构的影响有有利方面,也有不利方面。众所周知,徐变引起预应力钢筋混凝土结构的预应力损失;在大跨度梁中,徐变增加了梁的挠度。在这些结构中应尽量减小混凝土徐变。然而在水工大体积混凝土结构中,徐变能降低温度应力,减少收缩裂缝。在结构应力集中区徐变能使这些结构的应力重分布。因此在这些结构中,在保持混凝土强度不变条件下,要设法提高混凝土的徐变[1]。
由于徐变是混凝土的一种特殊属性,对水泥品种、骨料品种、水胶比、龄期(加荷龄期和持荷龄期)、荷载大小等多种因素比较敏感,因此根据徐变试验资料建立的徐变与加荷龄期 τ及持荷时间 t之间的关系式——徐变函数 C(t,τ)呈现高度的非线性,采用常规回归方法难以取得满意的效果[2]。对混凝土徐变规律的研究在混凝土结构应力、变形、预应力损失计算方面都有重要意义,徐变函数的精确与否直接影响到上述计算结果的精度。因此国内外学者在对大量的混凝土徐变资料进行分析、归纳和总结的基础上提出了多种徐变函数表达形式[3],比较有代表性的是幂函数式、对数函数式、双曲线函数式、指数函数式、指数和式、幂指数函数式以及多项函数式。其中朱伯芳院士于 1985年提出的幂指数函数徐变表达式[4]只需一个徐变公式就能表达徐变与加荷龄期及持荷时间之间的关系,使用非常方便,具有拟合精度高的优点,在工程界得以广泛应用。但幂指数函数徐变表达式也存在着待定系数多,计算工作量大的不足。随着计算机的普及应用,根据徐变试验资料,采用计算机计算程序计算徐变函数中的待定系数显得尤为重要,它不仅能摆脱复杂的手算,而且也使计算结果更为精确。
2 混凝土徐变函数的 EXCEL的计算
M icrosoft Excel是微软公司的办公软件的组件之一,是由 Microsoft为 W indow s和 Apple Macintosh操作系统的电脑而编写和运行的一款表格软件。Excel是微软办公套装软件的一个重要的组成部分,Excel中大量的公式函数可以选择应用,进行各种数据的处理和统计分析等,广泛地应用于管理、统计财经、金融等众多领域。采用 EXCEL进行列表试算徐变幂指数函数中的待定系数,能充分发挥Excel软件中的计算功能。
2.1 混凝土徐变幂指数函数表达式
朱伯芳院士于 1985年提出的幂指数函数徐变表达式如下:
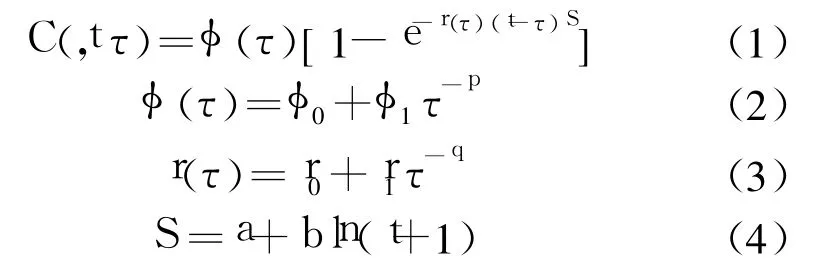
式中: C(t,τ)——混凝土徐变;
t——持荷时间;
τ——加荷龄期;φ0φ1,r0,r1,S,p,q,a,b— —试验常数,由试验资料确定。
徐变试验按加荷龄期分组进行,τi龄期加荷的徐变为:
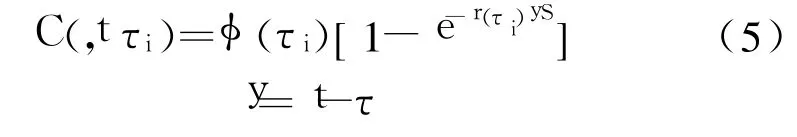
式中 φ(τi)是在 τi龄期加荷的最终徐变度,可采用持荷 720d以上龄期实测值或根据持荷 360d龄期实测值增加 5%进行估算。
对式(5)两边同时取对数,得:

再对式(6)两边同时取对数,得

以 lnρ(y)为纵坐标,lny为横坐标,试验值基本在一条直线上,由直线的截距可求出 r(τi),由直线斜率可求出 S。对于 n组徐变试验资料,重复以上计算,可得到 n组 φ(τi)、r(τi)和 S值。
当 τ→∞时,φ(τ)=φ0,绘制 φ(τi)-τi曲线,φ0值可列表试算。再由式(2)可知。

对于 n组试验资料进行回归分析,得出相关直线,直线的截距为 lnφ1,斜率为 p。采用类似列表试算的方法,可求出 r0,r1,q。
2.2 徐变幂指数函数的 EXCEL计算
结合某水电工程的混凝土徐变实测试验资料,采用 Excel软件进行混凝土徐变幂指数函数的计算。
图1为某水电工程混凝土的徐变试验资料。试验分别进行了 3d、7d、28d、90d、180d和 360d不同加荷龄期的测试,最长持荷时间为 360d。540d和720d的空格用于持荷时间超过 1年时的功能扩展,没有实测数据可以为空。由于没有超过 2年以上的徐变实测资料,因此混凝土的最终徐变值可根据360d龄期的实测值增加 5%进行估算。
根据式(6)和式(7),对实测试验值分别取两次对数,并进行回归分析计算,求出直线的截距r(τi)和斜率 S(见图2)。

图1 某水电工程混凝土徐变实测资料
根据式(8),用列表试算的方法,对 φ0取值进行回归分析计算,确定相关性最好的取值点,求出φ0、φ1、和 p值(见图3)。采用相同的列表试算的方法 ,求出 r0、r1、q值 (见图4)。
根据以上方法求出 φ0、φ1、r0、r1、p、q,S、a、b等公式参数,可得到该水电站混凝土实测徐变值的拟合函数表达式即式(9)。按照式(9)可求出徐变的计算值,并进行误差分析(见图5)。当相对误差小于 10%时,其拟合公式的精度可满足工程要求。
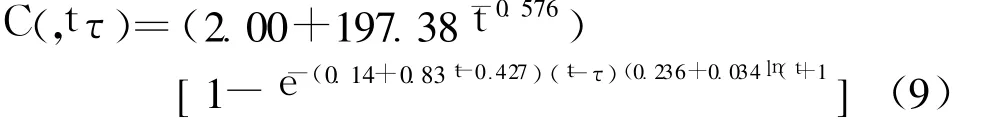

图2 采用回归计算 S值的 a、b常数

图3 采用试算法求 φ0、φ1和 p值

图4 采用试算法求出 r0、r1、q值

图5 拟合公式的误差计算
3 结 语
采用手工方式进行混凝土徐变函数表达式的拟合费时费力,且精度较低;而采用编程方式功能扩展性不强,也不利于试验技术人员掌握。在 EXCEL中采用试算列表法进行混凝土徐变函数表达式的拟合,使整个拟合过程变得非常简单,直观便捷,且拟合精度能够满足工程的要求。
[1]水利水电科学研究院结构材料所.大体积混凝土[M].北京:水利电力出版社,1990.
[2]何鲜峰,等.基因表达式及其在混凝土徐变分析中应用[J].重庆建筑大学学报,2008(4).
[3]惠荣炎,等.混凝土徐变[M].北京:中国铁道出版社,1988.
[4]朱伯芳.混凝土的弹性模量、徐变度与应力松弛系数[J].水利学报,1985(9).
