不可逆三热源制冷机的有限时间热力学分析

韩威 ，张广军 ，马迎秋 ，李忠建 ，陈建萍 ，叶倩

（1天华建筑设计有限公司；2中国天辰工程有限公司；3上海燃气工程设计研究有限公司；4联合技术研究中心（中国）有限公司；5上海市建筑科学研究院）

0 引言

最大制冷率及相应的性能系数是三热源制冷机（如吸收式制冷机、太阳能制冷机）的两个重要性能参数。前者决定了该制冷机的制冷率上界，而后者决定了它所允许的最佳性能系数的下界。在经典热力学理论中，可逆三热源制冷机可视为一个由可逆卡诺热机驱动的可逆卡诺制冷机的组合循环，其过程是在无限时间、无阻力、无温差的条件下进行的，这意味着该制冷机的制冷率为0。因此，经典热力学虽有重要理论意义，但却无法研究三热源制冷机中与制冷率有关的问题。另外，实际过程总是不可逆的，是在有限时间、有阻力、有温差的条件下进行的。

有限时间热力学理论能处理显含时间和与速率有关的变量的过程[1]，考虑了热力循环过程中不可逆因素（包括热阻、工质内部耗散等）的影响，其结果更具有实际的指导意义。近年来，不少学者应用有限时间热力学理论对不可逆三热源制冷机的最大制冷率及其相应的性能系数进行了研究[2-6]，但或者没有充分考虑其内不可逆性的影响，或者没有对热导率（或换热面积）进行更为一般的优化，因此所建立的表达式缺乏一般性。

本文利用有限时间热力学理论，通过对热导率的优化，导出了不可逆三热源制冷机制冷率上界及相应性能系数的一般表达式，并探讨了内不可逆性对这两个性能参数的影响，为实际三热源制冷机的优化设计提供了新的理论依据。

1 循环模型

不可逆三热源制冷机可视为一个由不可逆卡诺热机驱动的不可逆卡诺制冷机的组合循环，如图1所示。不可逆卡诺热机工作于高温热源TH和环境温度TO之间，其工质在两个等温过程的工作温度分别为Th和To；不可逆卡诺制冷机工作于环境温度TO和低温热源TL之间，其工质在两个等温过程的工作温度分别为To和Tl。由于工质和热源之间存在热阻，且循环在有限时间内进行，于是有Th＜TH、To＞TO、Tl＜TL。KH、KOH、KOL、KL为工质与相应的热源或环境之间的热导率。QH、QOH、QOL、QL为工质和相应的热源或环境之间的换热率。W既是热机的输出功率，也是制冷机的输入功率。

由图1，不可逆三热源制冷机的性能系数可定义为

式中η为不可逆卡诺热机的热效率；

ε为不可逆卡诺制冷机的性能系数。

根据热力学第一定律，有

设传热遵循牛顿定律，则有

除了外不可逆性（热阻）外，由工质内部耗散引起的内不可逆性也是热机或制冷机不可逆损失的重要来源。由热力学第二定律，并分别引入表示热机、制冷机内不可逆程度的参数Ihe、Ir，有下列关系

式中△Sh、△S1分别为等温过程Th、Tl中流入工质的熵流率；△Soh、△So1分别为热机和制冷机在等温过程To中流出工质的熵流率。Ihe=1、Ir=1分别表示热机、制冷机是内可逆的，即该三热源制冷机是内可逆的；0＜Ihe＜1、0＜Ir＜1分别表示热机、制冷机是内不可逆的，即该三热源制冷机是内不可逆的，且有Ihe、Ir越小，其内不可逆程度越大。

2 不可逆卡诺热机输出功率上界及相应的性能系数

在给定的热机总热导率下，其最大输出功率可通过拉格朗日乘数法求得。不可逆卡诺热机的最大输出功率为：

相应的热效率为

当Ihe=1时，该热效率等于CA效率[7]。

3 给定输入功率下不可逆卡诺制冷机制冷率上界及相应的性能系数

在给定制冷机的输入功率W和制冷机总热导率下，其最大制冷率可通过拉格朗日乘数法求得。不可逆卡诺制冷机的最大制冷率为

相应的性能系数为

4 不可逆三热源制冷机制冷率上界及相应的性能系数

当热机在最大输出功率的条件下驱动制冷机时，不可逆三热源制冷机可获得其最大制冷率。在给定的不可逆三热源制冷机总热导率下，其最大制冷率可通过拉格朗日乘数法求得。不可逆三热源制冷机的最大制冷率为

相应的性能系数为

当Ihe=Ir=1时，该三热源制冷机是内可逆的，于是，方程(14)和(15)可写为

式中Q＊L.max为内可逆三热源制冷机的最大制冷率；

COP＊为内可逆三热源制冷机取得最大制冷率时相应的性能系数。

方程（14）和（15）是在综合考虑了不可逆因子Ihe和Ir的基础上，通过优化热导率KH、KOH、KOL、KL后导出的，因此其形式是更为一般的。

5 结果与讨论

对于一个典型的不可逆三热源吸收式制冷机，TH=393K、TO=313K、TL=288K，Ihe=Ir=0.95，K=4kW/K，由方程和可得，它的最大制冷率QL.max=7.48kW，相应的COP=0.34。若有Ihe=Ir=1，即该吸收式制冷机是内可逆的，由方程和可得，它的最大制冷率QL.max=12.47kW，相应的COP=0.49。可见，循环的内不可逆性对该系统的最大制冷率及相应COP的影响很大。由方程（14）和（15）还可以看出，QL.max与K呈线性关系，而相应的COP与K值无关。

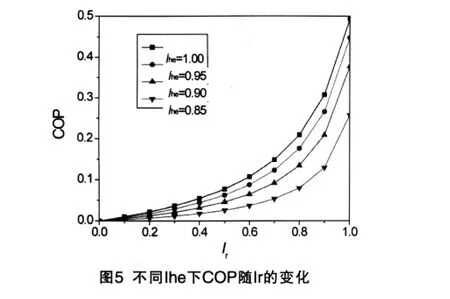
图2～5给出的是QL.max及相应的COP随Ihe或Ir的变化情况。可以看出，QL.max均随Ihe或Ir的增加而增大。其中，QL.max与Ihe近似呈线性关系，而随Ir增加而增大的速率先慢而后快。COP均随Ihe或Ir的增加而提高。其中，COP随Ihe增加而提高的速率先快而后慢，随Ir增加而提高的速率先慢而后快。

6 结论

利用有限时间热力学理论，建立了不可逆三热源制冷机模型。该模型考虑了有限速率传热（热阻）和工质内部耗散对系统性能的影响。通过对热导率的优化，导出了不可逆三热源制冷机制冷率上界及相应性能系数的一般表达式。由方程和可以看出，不可逆三热源制冷机的制冷率上界与总热导率呈线性关系，而其相应的性能系数与热导率无关。在对不可逆因子Ihe和Ir的研究中发现：尽管制冷率上界及相应的性能系数均随Ihe或Ir的增加而提高，但其变化的趋势却有一定的差别。

[1]陈金灿，严子浚.有限时间热力学理论的特征及发展中几个重要标志.厦门大学学报.2001,40(2):232-241.

[2]S.G ktun.Optimal performance of an irreversible refrigeratorwith three heatsources.Energy.1997,22(1):27-31.

[3]G.X.Lin and Z.J.The optimal performance of an irreversible absorption refrigerator.J.Phys.D:Appl.Phys.1997,30:2006-2011.

[4] J. C. Chen and J. A. Schouten.Optimum performance characteristics of an irreversible absorption refrigeration system.1998,39(10):999-1007.

[5]G.X.Lin and Z.J.Yan.The optimal operating temperature ofthe collector of an irreversible solar-driven refrigerator.J.Phys.D:Appl.Phys.1999,32:94-98.

[6]P.K.Bhardwaj,S.C.Kaushik and S.Jain. General performances of an irreversible vapour absorption refrigeration system using finite time thermodynamic approach. International Journal of Thermal Sciences,2005,44:189-196.

[7]F.L.Curzon and B.Ahlborn.Efficiency of a Canot engine at maximum power output.Amer.J.Phys.1975,43(1):22-24.