小角法在大坝视准线观测中的应用

刘武陵，罗琛

(1.湖南省常德市房地产产权管理处，湖南常德 415000； 2.中国葛洲坝集团股份有限公司测绘工程院，湖北宜昌 4430021)

小角法在大坝视准线观测中的应用

刘武陵1∗，罗琛2

(1.湖南省常德市房地产产权管理处，湖南常德 415000； 2.中国葛洲坝集团股份有限公司测绘工程院，湖北宜昌 4430021)

从观测思路、测点偏离值与位移量计算公式推导、精度分析等几方面阐述了小角法在长度不同的视准线观测中的灵活运用。

视准线；小角法；观测思路；公式推导；精度分析

1 前 言

视准线作为大坝监测的一种常用手段，越来越多地布设在大坝的坝顶、迎、背水面边坡、廊道等部位，用来监测大坝各高程面的水平位移，反映大坝不同高程面的变形趋势。

视准线是由端点和多个测点组成，视准线法是测定测点至由端点组成的直线的垂距(即测点偏离值)，测定测点偏离值常用的方法有活动觇牌法和小角法，活动觇牌法主要用于短距离视准线观测中，现运用得越来越少，普遍采用小角法观测。利用小角法观测视准线，必须观测距离和角度，距离精度对测点偏离值计算精度影响少，只需在首次观测时精确获取端点之间和端点至各测点的水平距离即可，周期观测不考虑水平距离的变化，测点偏离值的精度主要取决于角度观测精度，同时测点偏离值与端点周期观测间隔时间内是否发生位移有关，当端点在周期观测间隔时间内发生位移时，应利用周边已布设好的监测网点获取端点首次和某周期观测坐标值，通过首次和某周期观测坐标值相比计算端点在某周期的实际位移量，并将之加载至各测点某周期偏离值计算中，反之，当端点在周期观测间隔时间内无位移时，无需加载。

实际工作中，利用小角法观测视准线，当视准线长度在500 m以内时，成像较清晰，角度观测误差小，测点偏离值精度高；当视准线长度大于500 m时，角度观测误差相对大，测点偏离值精度难以保证。为此，结合几种情况阐述小角法在视准线观测中的灵活运用。

2 长度在500 m以内的视准线

2.1 观测思路

在视准线一端点A架设高精度仪器(测角标称精度1″或0.5″)，另一端点B和测点i上摆设固定觇牌或棱镜，先后照准端点B和测点i，观测∠BAi小角。

2.2 测点偏离值计算公式推导

如图1，A、B为视准线两端点，A′、B′为A、B某周期位置点，a、b为A、B的位移量；i为测点，i′为i在某周期的位置点，仪器架设在A′，α为测点i在某周期观测的角度；S1、S2分别为A至i、B至i点的水平距离，Li为测点某周期偏离值。

图1 长度在500 m以内的视准线示意图

测点i的周期偏离值为:

当a＝0、b＝0时，表示视准线两端点在周期观测间隔时间内没有发生位移，其测点i的周期偏离值为:

2.3 测点位移量计算公式推导

某周期测点位移量为首次偏离值与某周期偏离值的差值，其符号在规范规定向下游位移为正的基础上依据水流方向和具体测站点位来判断分析。

设α0为测点i在首次观测的角度，首次观测时不考虑端点位移情况，即a、b值为0，则测点首次偏离值为:

当架设仪器的端点(测站点)在水流方向的右侧，如图1，仪器架设在A′，测点i点不管分布在AB线的右侧(下游侧)还是分布在AB线的左侧(上游侧)，其位移量都为△i＝Li－Li0；反之，当架设仪器的端点(测站点)在水流方向的左侧，如图1虚线所示，仪器架设在B′，测点i位移量为△i＝Li0－Li。

2.4 精度分析

遵照规范和设计要求，视准线测点的埋设位置不得偏离两端点直线10 mm，因此sinα值非常小，sinα≈α″/ρ(ρ为常数，取206 265″)，故式(1)可简化为:

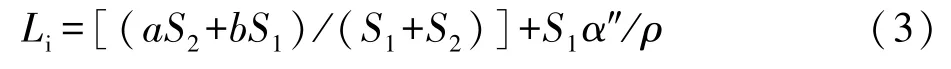
由于周期之间没有进行水平距离测量，S1、S2作为常数考虑，将式(2)、(3)化为中误差关系式可得:

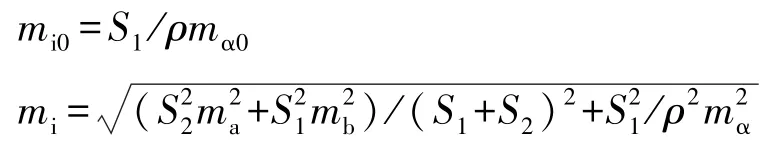
故:考虑首次观测连续观测两次，其测点位移量中误差关系式为:

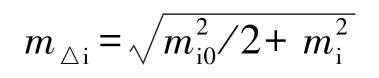
当S1＝S2＝250 m，ma＝mb＝±2 mm，mα0＝mα＝±0.7″时，m△i＝±1.75 mm。

3 长度大于500 m小于1 000 m的视准线

3.1 观测思路

在视准线中间部位选取一测点C作为临时端点，在C点上架设高精度仪器，在视准线两端点A、B和除C点外其余测点上摆放固定觇牌或棱镜，分别观测∠ACB大角和 AC、BC之间各测点的小角∠ACi、∠BCi。

3.2 测点偏离值计算公式推导

如图2，A、B为视准线两端点，A′、B′为A、B某周期位置点，a、b为A、B的位移量；C为临时端点，C′为C点某周期位置点；i为测点，i′为i在某周期的位置点，仪器架设在C′，α为测点i在某周期观测的小角度，β为临时端点在某周期观测的大角；S1、S2分别为A至C、B至C点的水平距离，Li为测点i某周期偏离值，LC为临时端点C某周期偏离值。

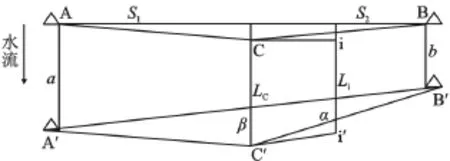
图2 长度大于500 m小于1 000 m的视准线示意图

临时端点C的周期偏离值为:

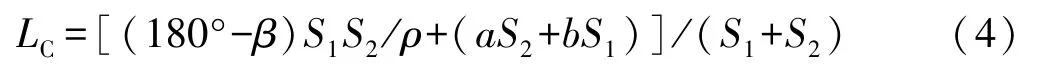
测点i的周期偏离值为:

当以B′(即水流方向的左端点)为后视测定CB方向上测点时，设SCi为C点到测点i的水平距离，SBi为B点到测点i的水平距离，其测点i的周期偏离值为:

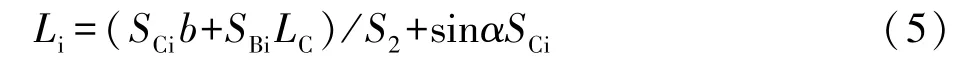
当以A′(即水流方向的右端点)为后视测定CA方向上测点时，设SCi为C点到测点i的水平距离，SAi为A点到测点i的水平距离，其测点i的周期偏离值为:

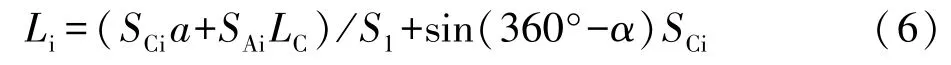
当a＝0、b＝0时，表示视准线两端点在周期观测间隔时间内没有发生位移，其临时端点C和测点i的周期偏离值为:

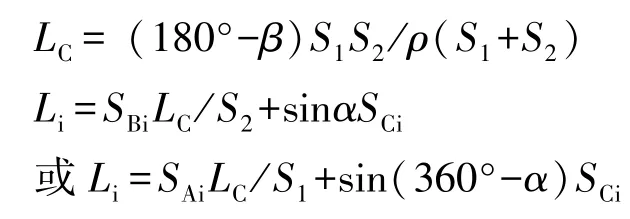
3.3 测点位移量计算公式推导

某周期测点位移量为首次偏离值与某周期偏离值的差值，其符号在规范规定向下游位移为正的基础上依据水流方向和具体测点点位来判断分析。

设α0、β0为测点i和临时端点C在首次观测的角度，首次观测时不考虑端点位移情况，即a、b值为0，则测点i和临时端点C首次偏离值为:

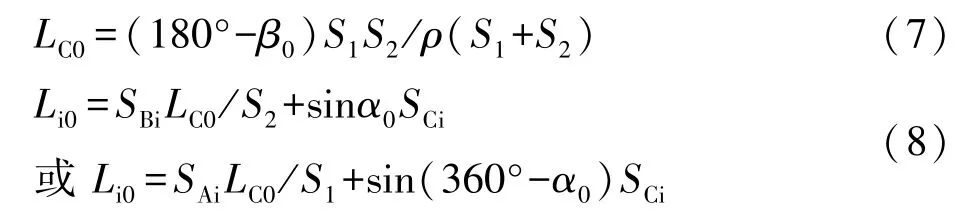
如图2所示，当C点、i点分别分布在AB、CB线的右侧(即下游面)和i点分布在CA线的左侧(即上游面)时，C点位移量为:△C＝LC－LC0，i点位移量为:△i＝Li－Li0；反之，C点位移量为:△C＝LC0－LC，i点位移量为:△i＝Li0－Li。

3.4 精度分析

遵照规范和设计要求，视准线测点的埋设位置不得偏离两端点直线10 mm，因此sinα、sin(360°－α)值非常小，sinα≈α″/ρ、sin(360°－α)≈(360°－α)/ρ(ρ为常数，取206 265″)，故式(5)、(6)、(8)可简化为:

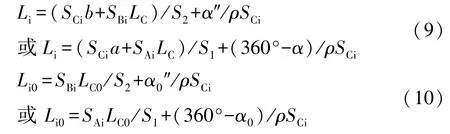
由于周期之间没有进行距离测量，S1、S2、SCi、SBi、SAi作为常数考虑，将式(4)、(7)、(9)、(10)化为中误差关系式可得:

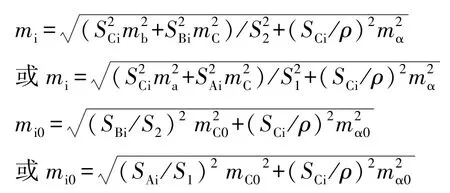
故:考虑首次观测连续观测两次，测点位移量中误差关系式为:

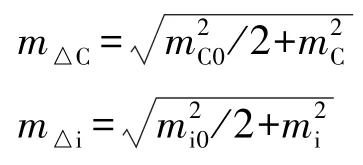
当S1＝S2＝500 m，SCi＝SBi＝SAi＝250 m，ma＝mb＝±2 mm，mα0＝mα＝mβ＝mβ0＝ ±0.7″时，m△C＝±1.75 mm，m△i＝±1.69 mm。

4 长度大于1 000 m小于1 500 m的视准线

4.1 观测思路

在视准线1/3、2/3部位各选取一测点作为临时端点，通过周边监测网点获取临时端点某周期坐标，计算临时端点某周期偏离值，分别在临时端点上架设高精度仪器，在相邻的端点或临时端点及除临时端点外的其余测点上摆放固定觇牌或棱镜，分别观测临时端点至端点、临时端点至临时端点之间各测点的小角。

4.2 测点偏离值计算公式推导

如图3所示，A、B为视准线两端点，EF为与坐标轴平行的直线线，设其为视准线端点和所有测点偏离值计算的基准线，A′、B′为A、B某周期位置点，a、b为A、B某周期偏离EF线的偏离值；C、D为任选的临时端点，C′、D′为C、D某周期位置点；i为测点，i′为i在某周期的位置点，仪器架设在C′或D′，α为测点i在某周期观测的小角度；Li为测点i某周期偏离值，LC、LD为临时端点C、D某周期偏离值。

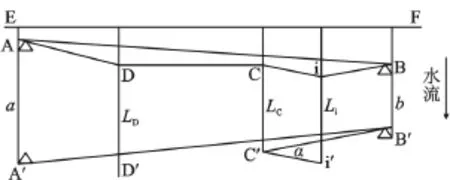
图3 长度大于1 000 m小于1 500 m的视准线示意图

A、B、C、D的偏离值a、b、LC、LD是通过周边监测网点获取其坐标值后直接计算所得；测点的偏离值是通过分别在C′、D′架设仪器分段观测其小角计算所得，其偏离值为:

当仪器架设在C′，分别后视B′、D′时，其偏离值与式(5)、(6)相同，即:

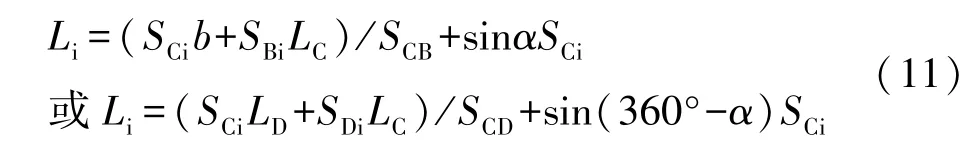
其中:SCB为C至B的水平距离，SCD为C至D的水平距离，SDi为D至i的水平距离。

当仪器架设在D′，后视A′时，其偏离值与式(6)相同，即:

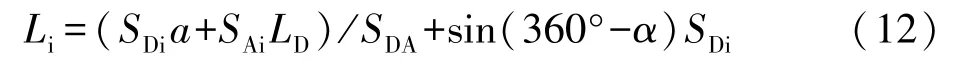
其中:SDA为D至A的水平距离，SAi为D至i的水平距离。

当a＝0、b＝0时，不影响CD线上测点偏离值，只对CB、DA线上测点偏离值产生影响，表示视准线两端点在周期观测间隔时间内没有发生位移且AB线与EF线重合，其测点的周期偏离值为:

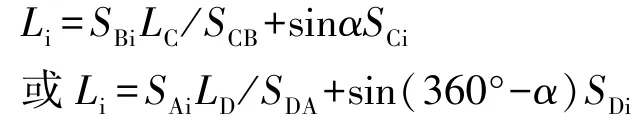
4.3 测点位移量计算公式推导

某周期测点位移量为首次偏离值与某周期偏离值的差值，其符号在规范规定向下游位移为正的基础上依据水流方向和具体测点点位来判断分析。

设α0为测点i在首次观测的角度，a0、b0为A、B首次偏离值，首次观测时考虑端点不位移且考虑实际工作中AB线不可能与EF线重合情况，即a0≠0，b0≠0，故测点i首次偏离值为:

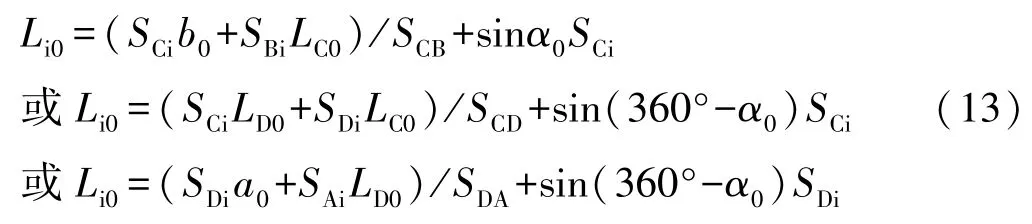
如图示3所示，当i点分别分布在CB的右侧(即下游面)和CD、DA线的左侧(即上游面)时，i点位移量为:△i＝Li－Li0；反之，i点位移量为:△i＝Li0－Li。

4.4 精度分析

遵照规范和设计要求，视准线测点的埋设位置不得偏离两端点直线10 mm，因此sinα、sin(360°－α)值非常小，sinα≈α″/ρ、sin(360°－α)≈(360°－α)/ρ(ρ为常数，取206 265″)，故式(11)、(12)、(13)可简化为:

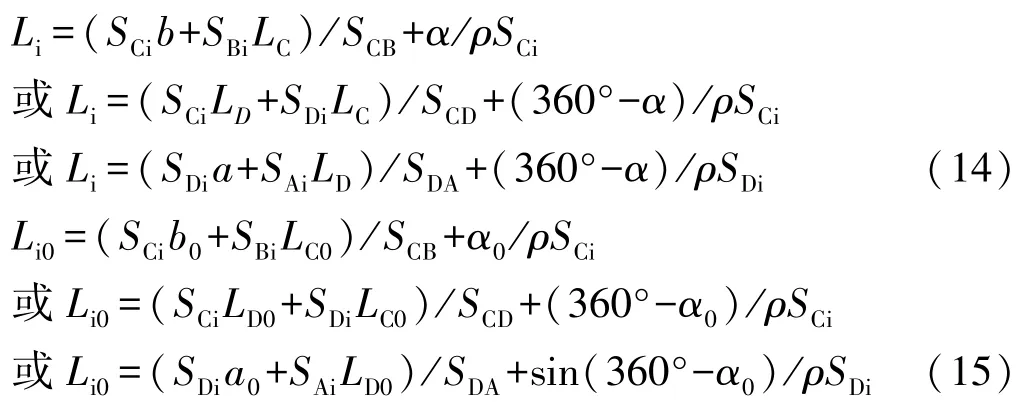
由于周期之间没有进行水平距离测量，SCD、SCB、SDA、SCi、SBi、SAi、SDi作为常数考虑，将式(14)、(15)化为中误差关系式可得:

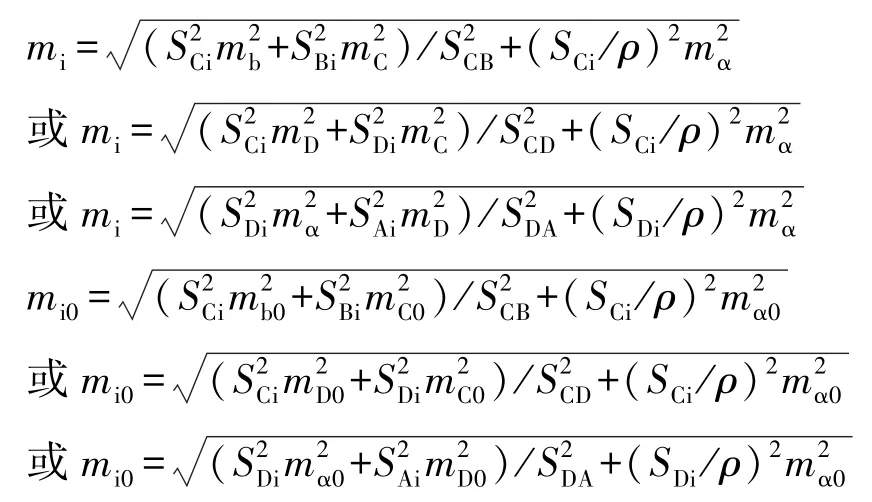
故:考虑首次观测连续观测两次，测点位移量中误差关系式为:

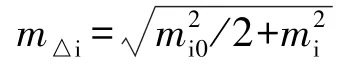
当:SCB＝SCD＝SDA＝500 mSCi＝SBi＝SAi＝SDi＝250 mma＝ma0＝mb＝mb0＝mC＝mD＝mC0＝mD0＝±1.63 mmmα0＝mα＝±0.7″时，m△i＝±1.44 mm。

当视准线长度大于1 500 m时，其观测思路、测点偏离值与位移量计算公式推导及精度分析与长度大于1 000 m小于1 500 m的视准线相同，不同之处在于对长度大于1 500 m的视准线须选取3个或3个以上测点作为临时端点，分段观测的段数增加了。

5 结 语

本文针对不同长度视准线总结了小角法在视准线观测中的应用情况，目前已广泛运用于实际工作中，对大坝监测起到了良好的效果。

[1]DL/T5178－2003.混凝土坝安全监测技术规范.

[2]李青岳，陈永奇.工程测量学[M].北京:测绘出版社，1995

Application of Small－angle Method on Dam Alignment Observations

Liu WuLing1，Luo Chen2
(1.Changde City，Hunan Province Real Estate Property Management Office，Changde 415000，China；2.China Gezhouba Group Co.，Ltd.Surveying and Mapping Engineering Institute，Yichang 443002，China)

This article elaborate on the application in a flexible way of small angle measurement in the varying collimation line observation of length，which from observational thoughts＼deviation value of measuring point＼equation derivation to calculate the displacement and precision analysis etc.

Collimation line；Small－angle method；Observation ideas；Formula derivation；Accuracy Analysis

1672－8262(2010)03－97－04

P258

B

2009—11—10

刘武陵(1975—)，男，工程师，主要从事工程测量、数据处理、数字化制图等方面的工作。