天然气管网定线研究
2010-04-17沈致和
王 鑫 沈致和
集输管网的优化,是一个多学科互相交叉运用的课题,涉及到最优化、运筹学、图论方面的数学理论、技术经济评价以及如何通过计算机实现优化的问题等方面。天然气集输管网系统的优化设计主要解决以下三个问题:1)布局优化问题:确定网络的拓扑形式,即确定管网连接形式以及布站方式;2)位置优化问题:确定中间站的位置;3)参数优化问题:确定各管径、壁厚等参数。
将各个子问题统一起来,求得整个天然气集输管网系统的优化设计方案。
本文研究了国内外天然气设计的成果,在此基础上重点讨论了天然气调压站布局和天然气管网布线及管网的水力计算。尝试用新的思路简化复杂的天然气布局最优化问题,并基于贪心算法,图论中的最短树思想使用C++软件编制了一套程序,定量分析了一个工程实例中遇到的调压站选址问题及其布线问题。
1 天然气管网定线作用
一般来说天然气管网定线问题包括两个部分:1)选择在一个城镇的道路管网中,哪些道路铺设天然气管网。很显然并不是所有的道路都需要铺设天然气管网,这一点在人口密度相对稀疏的地区尤其明显,在人口稠密的地区,天然气管线繁多,天然气管网的铺设更多考虑根据用气区的用户分布,然后按街道形状布置。而人口稀疏的地区天然气管网也相对稀疏,在这种情况下管网的定线,对整个天然气管网设计的经济性都有非常大的影响。2)选择调压站的数量,位置,作用半径。我们把天然气管网的初投资大致分为:管网投资+调压站投资。调压站是天然气管网不同于其他管网的一个显著特点,它连接中压天然气管道和低压天然气管道。相对于低压管网而言,我们可以把各个调压站看作一个个气源。而每一个小气源的作用半径都是有限的,而且气源的位置对管道的布线显然也有影响。所以如何确定调压站的个数、位置,使得管道和调压站之间达到比较协调的组合是我们要考虑的第二个问题。
2 实例演示
图1的背景是一个城镇的道路图,因为天然气管道是沿着道路铺设的,所以我们把道路模型提炼出来,将各个节点标注,并注明各个节点之间的距离。
2.1 问题描述
天然气管道布局的最优化问题可简略的概括为:在保证所有用户都能正常用气的情况下,使总投资最省。总投资包括两个方面:1)调压站投资;2)管道投资。
这两项投资是此消彼长的关系,我们可以想象一下如果只先用一个调压站,那么只有把几乎所有道路都铺设管道才能达到每个用户用气的目的。这样管道的投资必然是最大的,但相反使调压站的投资变得最小。反之亦然增加调压站投资,但可以减少管道的投资。
2.2 三个假设
为了使得下一步优化分析得以进行,有必要先提出三个假设:
1)确定网络图的权值,假设存在平均管道价格。根据山东阳谷恒泰实业有限公司的SDR17.6,de40管价格为 4.32元/m,我们先假定低压干管平均价格采用de40管的价格(如果在水力计算时发现假定管径平均值和计算出入较大,可修改该数值),加上开挖填埋费用6元/m,故总管道费记作10.32元/m。
2)调压站价格,根据河北鑫星调压器有限公司出品的RTZ-31FQ型燃气调压箱,输出管径DN32~DN63,价格为2 000元,我们采用两台调压器串联组成的工作监控调压器,加上配套设施,一个调压站价格记为5 000元。
3)家用煤气灶的额定压力为784 Pa或980 Pa。为达到这一标准,《城镇燃气与热能供应》建议调压站的作用半径(管道距离)不宜超过500 m,为此,我们假定在给弱尔镇的天然气管道布局设计中,调压站的作用半径不得超过550 m。
2.3 使用Prim算法求最短生成树
假定N=(V,E)是连通图。其中,V为节点集合;E为边集合;集合 TE为N上最小生成树上的边,初始 TE=NULL。
1)初始化:任选一节点 u0,U={u0},TE={}。
2)对所有的 u∈U,v∈ V-U 的边(u,v)∈E中选择距离最小的边(u0,v0),将此边并入集合 TE中,同时v0进入集合U中。
3)循环执行步骤2直至U=V,此时 TE中必定只有n-1条边,则此时的 T=(V,TE)就是 N上的最小生成树算法编程,得到最短树图如图1所示。

2.4 深度优先遍历
第一步:基于最小生成树 T的深度优先遍历处理:
假定气源站集合为RC,RC初始集合为最小生成树T上的所有非叶子节点。每个节点有两个变量:sd(初始为0)和cd(初始为0)。其中,如果该节点可以被删除,则 sd=1,否则sd=0;cd为孩子节点中可以被删除的个数。
第二步:对 T进行第一次深度优先遍历,对每个非根非叶子节点x作如下处理:
节点 x的父亲节点为 f,孩子节点集合为 cc,那么如果 f与 cc中节点距离都小于550 m,那么则该节点 x→sd=1,f→cd++。
对T进行第二次深度优先遍历,对每个非根非叶子节点 x作如下处理:
如果 x→sd==1并且 x→cd<=x→sd,那么就将节点 x从RC中删除。
做如此判断主要是为了防止将一个节点删除后,其多个原本符合条件的孩子节点反而不可以被删除了。
最终得到的RC就是需要建立的气源站。
2.5 算法编程
编程按三步来进行,参考上述算法:
1)初始化所有节点,并对其进行赋值。
2)进行两次深度优先遍历,第一次删除不需要的节点,第二次检验上次的节点以免误删。
3)根据已给出的调压站,管道价格,计算最终花费。
2.6 选取调压站
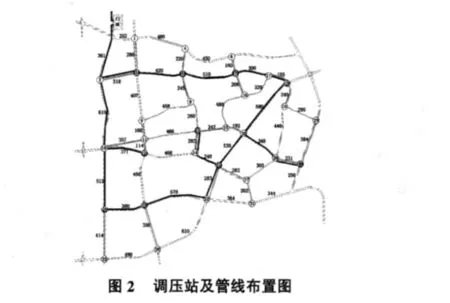
选择调压站节点为:站点 3,站点5,站点7,站点9,站点12,站点13,站点 18,站点 21,站点23,站点 24,站点27,站点 29,站点 30。
删除在调压站作用半径之内出现相邻调压站。站点21与站点27相邻,站点 30与站点29相邻,站点3与站点9相邻。比较附近管线的权值,删除站点27,站点29,站点9。
最后,布置中压管线,使中压管线距离各个调压站距离最短。
总体管线布置图如图2所示。
3 结果分析
城镇燃气管网的布置,调压站的选址,数量,现大多根据城市道路小区建设情况,按经验估计,或者采用图上作业法。
使用计算机对其进行定量分析,国内外论文讨论较少。本篇论文以图论作为基础,探讨了燃气管网布置中的一些问题,并针对具体工程做了详细的说明和计算,对比原来规划结果,可以发现投资有所减少。
所发现的问题:1)本文实例所处的地区,地广人稀,用户较少,管径变化不大,但是在人口密集的地区,从整个城镇出发,各个分支管网的管径变化很大,很难求出所谓的平均管道费用,这样就可能出现后续计算和假设不符,大大增加工作量。2)本文算法2中采用的深度优先遍历实际上是贪心算法的一种,贪心算法的特点是求出的解是较优解,很有可能不是最优解。
以上两点是本文的不足,可以看出本文还只是肤浅的探讨,尚需更深入的研究。
[1] 彭继军,田贯三,刘 燕.燃气管网图的计算机生成[J].山东建筑工程学院学报,2003(18):58-62.
[2] GB 50028-93,城镇燃气设计规范[S].
[3] 严煦世,赵洪宾.给水管网理论和计算[M].北京:中国建筑工业出版社,1986.
[4] 杨立民.燃气长输管线末段储气的研究与计算[D].哈尔滨:哈尔滨建筑大学硕士论文,1995.
