基于光平面的轨距测量方法*

郑树彬 柴晓冬 韩国阁 李立明

(上海工程技术大学城市轨道交通学院,201620,上海∥第一作者,博士)

轨道不平顺主要包括轨道高低、轨向、水平、三角坑以及轨距等一系列不平顺参数,其中轨距是最基本的轨道不平顺参数之一。严重的轨距不平顺会导致列车掉道或卡轨,降低轨道及车辆的寿命,危害行车安全。因此,对轨距进行快速、精确的检测具有重要意义[1]。早期的动态轨距测量采用滚动轮接触轨头的方法。这种接触式方法机械惯性大、精度低,在准高速动态测量时无法使用。而在准高速轨道检测车中采用的基于多机器视觉的轨距检测系统,其图像采集、分析、处理和计算量大,对于高速轨道检测造成较大的挑战[2]。基于光平面的单目机器视觉在物体定位、空间物体三维重构及测距等领域有着广泛的应用。本文提出将光平面单目机器视觉技术应用于轨距的检测当中,可有效实现轨距参数的非接触动态测量,提高检测效率,降低检测成本。

1 测量原理

在左右钢轨内侧各架设一台 CCD(电荷耦合器件)摄像机(左右侧摄像机分别记为 Cl和 Cr)和扇形光源激光器;激光器射出的扇形光面照在钢轨上形成一条清晰的光带,CCD摄像机采集带有光带的轨道图像,经过图像处理提取光带,获得轨道截面轮廓线,如图 1所示。光平面可表示为:

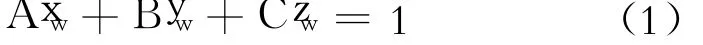
式中系数 A、B、C可由定标得出。轨道轮廓线在该光平面内,则轮廓线上任意一点(xi,yi,zi)都在光平面内。

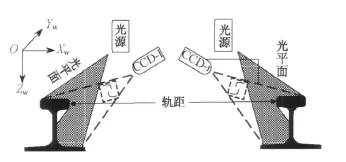
图 1 轨距测量原理

如图 1所示,轨距测量系统由左右两侧的光平面测量子系统构成。本文以左侧轨道的光平面测量子系统进行论述。记轨道轮廓线上任意一点的图像坐标为(ul,vl),将该测量子系统的世界坐标系建立在摄像机的光心上,则摄像机坐标系与世界坐标系重合,摄像机坐标系与世界坐标系不存在旋转和平移的关系。令 Rl和 Tl分别为旋转矩阵和平移向量,则摄像机外参数矩阵为单位矩阵([Rl,Tl]=I),因此其投影矩阵 Ml=Al[Rl,Tl]=Al。其中 Al为摄像机内部参数,由摄像机定标得出。由摄像机投影原理有:

世界坐标点(xwl,ywl,zwl)在光平面上,满足光平面方程,而世界坐标系固定于左侧摄像机光心上,有zcl=zwl,故由式(1)和(2)联立可得:

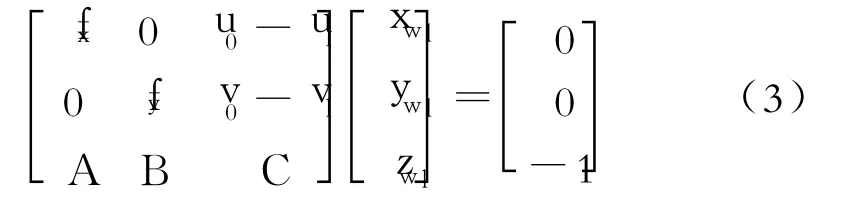
其中,fx、fy是摄像机的有效焦距,(u0,v0)是图像中心坐标。上述量均是内参数矩阵 Ml中的元素。由式(3)可求出世界坐标点(xwl,ywl,zwl)。

同理,对于右侧轨道的光平面测量子系统,将该测量系统的世界坐标系建立在摄像机的光心上,则也存在式(3)的关系,因此可求出右侧轨道轮廓线图像点(ur,vr)所对应的世界坐标点(xwr,ywr,zwr)。

另外,通过系统定标可获得左右摄像机的空间几何关系 Rl,r和 Tl,r。因此可将(xwl,ywl,zwl)和(xwr,ywr,zwr)统一到同一世界坐标系下,在同一世界坐标系下根据空间两点距离公式求出轨距值。

2 定标

基于光平面的轨距检测方法通过 CCD摄像机获取轨道状态信息,图像上任意一点的位置与轨道相应点的几何位置有关。这些位置的相互关系,由摄像机成像几何模型(摄像机参数)所决定。确定这些参数的过程即是定标。本方法除了单部摄像机定标以外,还需进行两方面的定标:一是对光平面进行定标,以确定光平面参数;二是对轨距检测系统进行定标,以确定左右钢轨摄像机之间的几何关系,以便将左右钢轨轨距点的世界坐标系转换到同一世界坐标系下。

2.1 光平面定标

光平面方程的系数是通过光平面上已知的一系列特征点的世界坐标来确定的。将扇形光源射出的光照在标定靶上,前后移动标定靶,可以得到 m(m＞3)个光线上的点的坐标(xwi,ywi,zwi)(i=1,2,…,m)。将这些点的坐标代入光平面方程,则有:

由式(4)可得到该平面法向量的3个分量A、B、C的最小二乘解。对于标定靶上特征点的世界坐标的确定,传统上有直接法和间接法两种。直接法是直接读取光带上特征点的世界坐标进行定标[3]。间接法则利用标定靶特征点和对应的世界坐标来完成定标[4-5]。本课题采用间接法来获得标定靶上特征点的世界坐标。对于左侧轨道的光平面测量子系统,定标时添加一台辅助 CCD摄像机,与子系统的摄像机构成双目视觉系统,来实现特征点世界坐标的获取。左右侧辅助摄像机分别记为 Cl′和 Cr′。以左侧钢轨测量子系统为例,记辅助摄像机 Cl′的内部参数为 Al′,该双目摄像机之间的几何关系为 Rl,l′和Tl,l′,将双目视觉系统的世界坐标系原点也定于摄像机 Cl的光心上,则它们的投影矩阵分别为 Ml=AlI=Al(I为单位矩阵 ),Ml′=Al′[Rl,l′,Tl,l′],则摄像机投影关系有:

zcl、zcl′为空间点在摄像机坐标中的分量,在计算时可消去 ;(ul,vl)和(ul′,vl′)分别为摄像机 Cl和 Cl′所拍摄图像中同一特征点 P的图像坐标,通过图像分析匹配得到。由立体视觉三维重建理论可知,通过式(5)和式(6)可求得 P的坐标(xwl,ywl,zwl)[6]。通过该方法可得到 m个特征点坐标,代入式(4)可计算出光平面方程系数 A,B,C,此时光平面上的点就是以建立在摄像机 Cl光心的世界坐标系来表示的。同理,对于右侧钢轨的光平面上的点,则通过建立在摄像机Cr光心的世界坐标系来表示。

2.2 轨距检测系统定标

由于左右两侧光平面方程的世界坐标系是建立在各自测量子系统的摄像机 Cl和 Cr的光心上的,而轨距测量点需要在同一世界坐标系中表示,因此还需要对两侧的摄像机的空间几何关系进行定标。由于摄像机是背对背安装的,使得 Cl和 Cr摄像机视场没有交集,同一个特征点不可能同时被两者采集到,因此需要做一特定的标定板,使得 Cl和 Cr各自采集到的图像特征点具有一定的几何关系。系统定标示意图如图 2所示。

图 2 系统定标示意图

由单摄像机定标可获得 Cl和 Cr的外部参数为[Rl,Tl]和[Rr,Tr]。这些外部参数的世界坐标系建立在图 2所示的模板上。由摄像机的投影关系有:

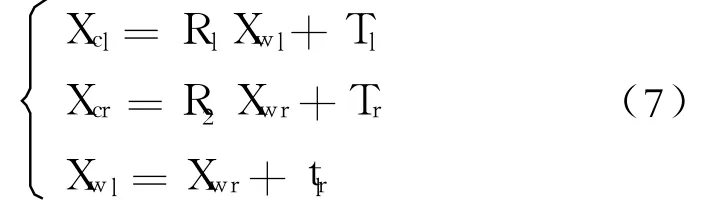
式中:

Xcl、Xcr— —空间点 Pl和 Pr(Pl和 Pr为模板上的角点)分别在左右摄像机坐标系中的坐标;

Xwl、Xwr—— Pl和 Pr在建立于模板左右侧的世界坐标系中的坐标(见图 2);

tlr——Xwl和 Xwr的平移向量,由模板可知 tlr为已知量。

因此,由式(7)可获得摄像机 Cl和 Cr的空间几何关系为:

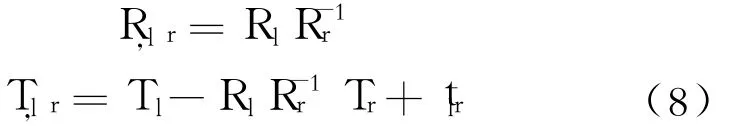
通过式(8)可将左右钢轨的光平面空间坐标点统一到同一世界坐标系中,轨距即可由空间距离公式求出。

3 试验验证分析

3.1 光平面定标试验

试验采用德国 AVT CCD摄像机,图像分辨率为1280×960,激光光源是波长 635mm的激光器。将标定靶放在三维工作台上,激光器发射光源打在标定靶上,移动标定靶,获取不同位置的定标图像(见图 3)。

图 3 光平面定标

试验中,从红色光线上读取棋盘格黑白交叉点作为标定光平面方程的特征点,读取 m个特征点,按间接定标的方法,计算得出光平面参数值。表 1为通过 4次试验得到的定标结果,每次 m的取值均不同。由表 1可知,由于 A、B、C是采用最小二乘法得出的优化解,因此用不同特征点组合求光平面法向量的系数时,其结果基本一致,仅存在较小的偏差,定标结果具有很好的稳定性。

表 1 光平面定标结果

3.2 轨距测量试验

在光平面方程定标后,以三维坐标工作台的某个位置为起始点,调节两钢轨之间的距离变化值,用表 1获得的光平面方程,通过轨距算法进行计算,获得试验数据(见表 2)。

由表 2可知,同一光带上定标出的光平面方程,对测量结果影响很小,且测量值具有良好的重复性。表中最大测量误差为 0.286mm,而一般轨道轨距将误差控制在(-2mm,+6mm)范围内。中国准高速轨检车 GJ-5关于轨距的检测精度为 0.8mm,因此,基于光平面的轨距检测可满足轨距测量测试精度的要求。另外,试验中采用的光源照射在轨道中形成的光带较粗(0.8mm),且定标靶的精度不高(0.1mm)。如果能提高光源和定标靶的精度,则可获得更高的定标精度,从而获得更高精度的测量结果。

表 2 轨距变化值试验结果

4 结语

轨道状态在实际使用过程中受到诸多因素的影响,而严重的轨距不平顺影响列车运行的安全性和舒适性,因此,及时准确掌握轨距不平顺量是非常必要的。本文提出的基于光平面的轨距测量方法,具有精度高、重复性好的特点,且相对于其它机器视觉的轨距检测系统,该测量方法只采用了两部摄像机,减少了图像采集、分析和处理的数据量;而基于光平面的三维坐标值求解更直接,运算量更少,可有效加快检测速度。

[1] 余祖俊.轨道交通线路几何安全状态动态检测技术研究[D].北京:北京交通大学,2008.

[2] 刘铁,任盛伟,许贵阳,等.GJ-4型轨检车轨距-轨向检测系统改造[J].中国铁道科学,2006,27(6):137.

[3] 霍龙,刘伟军,张爱军.视觉测量中光平面的标定方法研究[J].计算机测量与控制,2005,13(7):621.

[4] 刘伟军,刘鹏,齐越.一种基于视觉的自由曲面三维测量系统[J].小型微型计算机系统.2003,24(12):2170.

[5] Shahriar N.Epipolar geometry of opti-acoustic stereo imaging[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,2007,29(10):1776.

[6] 马颂德,张正友.计算机视觉—计算理论与算法基础[M].北京:科学出版社,2003.