基于线性自抗扰控制器和磁通观测器的异步电机调速系统

刘丽英，李小鹏，张国香，李春华，王东涛

LIU Li-ying1,2, LI Xiao-peng1, ZHANG Guo-xiang1, LI Chun-hua1, WANG Dong-tao1

（1. 天津工程师范学院 自动化与电气工程学院，天津 300222；2. 天津职业技术师范大学 天津市信息传感与智能控制重点实验室，天津 300222）

基于线性自抗扰控制器和磁通观测器的异步电机调速系统

A sensorless vector control induction motor drive based on ladrc and fl ux observer

刘丽英1,2，李小鹏1，张国香1，李春华1，王东涛1

LIU Li-ying1,2, LI Xiao-peng1, ZHANG Guo-xiang1, LI Chun-hua1, WANG Dong-tao1

（1. 天津工程师范学院 自动化与电气工程学院，天津 300222；2. 天津职业技术师范大学 天津市信息传感与智能控制重点实验室，天津 300222）

针对异步电机难以建立精确的数学模型和采用PI调节器的矢量控制系统参数鲁棒性差的问题，将线性自抗扰控制器引入异步电机调速系统中。线性自抗扰控制器不需要电机的精确数学模型，通过线性扩张状态观测器估计出电机模型中的耦合项及参数摄动等引起的总扰动并加以补偿，实现了磁链和转矩的完全解耦。针对磁通观测器对转子电阻的鲁棒性差的问题，文中引入一个建立在旋转坐标系中的磁通观测器，结构简单，对转子电阻具有固有的鲁棒性。在观测磁通的基础上，根据矢量控制理论，采用q轴磁通收敛于零估计转速，从而建立了无速度传感器矢量控制异步电机调速系统。仿真结果表明此控制方案具有很好的动、静态性能，且对负载扰动、电机参数变化等具有很强的鲁棒性。

异步电机；无速度传感器矢量控制；线性自抗扰控制器；磁通观测器；速度估计；鲁棒性

0 引言

高性能矢量控制交流调速系统中需采用速度闭环控制，异步电机的矢量控制调速系统通常是通过测量转速来实现的，然而，速度传感器增加了系统成本，存在安装与维护的困难，降低了系统的可靠性，且不适用于恶劣环境。理论上通过异步电机的电压和电流可以推算出转速，从而可以不使用速度传感器。目前的无速度传感器控制方法主要有开环估计法、利用定子三次谐波电压估计、利用电机凸极效应估计、模型参考自适应法、扩展卡尔曼滤波法以及人工智能方法等[1,2]。其中，模型参考自适应法由于稳定性好和计算量小，是转速估计的重要方向之一。本文采用的转速推算法近似于MRAS，但它是建立在旋转坐标系中，比MRAS方法更简便[3]。

目前，PID是异步电机调速系统中主要采用的控制器，但它容易受系统参数变化影响，为此，韩京清提出了自抗扰控制器[4]。自抗扰控制器是在吸取PID控制的优点，克服其缺陷的基础上提出的一种新型控制器，它不依赖于被控对象的精确数学模型，能实时估计系统在运行过程中受到的各种外部与内部扰动的总和并加以补偿，从而使系统线性化为积分串联型结构。从而提高了系统的性能。文献[5]和[6]将自抗扰控制器（ADRC）引入电机调速系统中。

然而, 自抗扰控制器有多个参数需要整定，参数作用方向又无法确定，在工程中应用时参数调整过程复杂。虽然文献[7]和[8]对自抗扰控制器参数整定问题进行了探讨，但还没有形成系统的整定方法，因此若能减少自抗扰控制器的参数，简化参数整定过程，将有助于工程实用化。为此，文献[9]提出线性自抗扰控制器。本文将线性自抗扰控制器应用于异步电机调速系统中，线性自抗扰控制器继承了自抗扰控制器的优点，能够解决电机难以建立精确数学模型以及电机参数变化、外部干扰等对系统性能的影响，使系统的磁链与转矩实现完全解耦，从而提高系统的性能，但需要调整的参数减少了。

1 线性自抗扰控制器

下面以二阶线性自抗扰控制器构成的系统为例说明线性自抗扰控制器的原理。设一类不确定对象为：

式(2)写成状态方程形式如式 (3)所示。

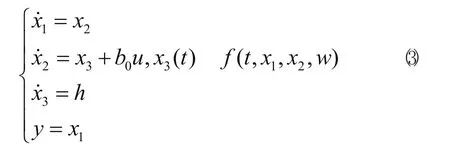
其中，x3=f是未知的被扩张的状态变量，h(t)是f(t)的导数，f是未知的。 能够由状态观测器(4)估计出来，称其为线性扩张状态观测器（LESO）。

只要合理选取观测器增益β1, β2, β3，这个状态观测器的各状态变量zi(t)将分别跟踪系统(3) 的各状态变量xi(t)，也就是：

忽略z3(t)对的估计误差，被控对象可简化为一个双积分串联结构。

它很容易由式(7)表示的PD控制器控制。

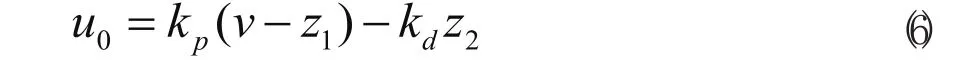
其中v是给定信号， kp，kd为控制器增益。

方程式(4)、(5)和(6)，组合在一起能估计出总扰动并加以补偿，因此被称为线性自抗扰控制器(LADRC)，它的结构如图1所示。

图1 线性自抗扰控制器结构图

2 系统设计

2.1 控制器设计

基于转子磁场定向理论，笼式异步电动机在同步旋转坐标系下的动态模型可用四阶非线性微分方程来描述[5]。

其中，

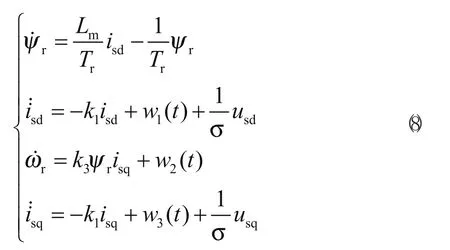
为了使电机运行过程中不致过流, 必须对励磁电流和转矩电流进行限幅控制, 因此采用图2所示的转子磁场定向双闭环控制方案, 即采用四个一阶LADRC分别调节。

图2 系统框图

分析方程式(4)，(5)和(6)，我们得到d轴定子电流的一阶LADRC如下。

2.2 转子磁通观测器

在上述系统中, 转子磁通由式(9)和(10)来估算，称为转子磁通观测器。

其中Tc是转子磁通观测器增益的倒数。

在图2中，若速度的估算值正确，则ψrd=ψr，q轴转子磁通收敛于零。根据这一内在关系，本文利用q轴转子磁通收敛于零来估算转速，如下式所示。

其中Kω是比例系数，Tω是积分时间常数。

这种速度估算方法类似于常规的MRAS, 但是它是建立在旋转坐标系上，更简单。

3 仿真研究

为了验证采用线性自抗扰控制器后异步电机调速系统的性能，在MATLAB/SIMULINK中进行仿真研究。重点研究空载起动、突加负载、转子电阻摄动和转动惯量变化下系统的性能。电机的参数如表1所示，仿真波形如图3、4和5所示，图中的转速为标幺值，nbase=1460r/min。

表1 电机参数1

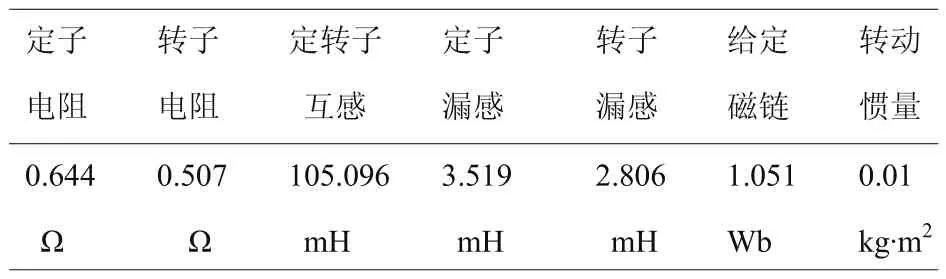
表2 电机参数2

在实际应用中，系统中需要给定积分器和限幅器，本系统中，四个线性自抗扰控制器都包含有给定积分器和限幅器。其中，用线性跟踪微分器（LTD）作为给定积分器，一阶LTD的表达式为；电流的幅值为20A，电压的幅值为340V。

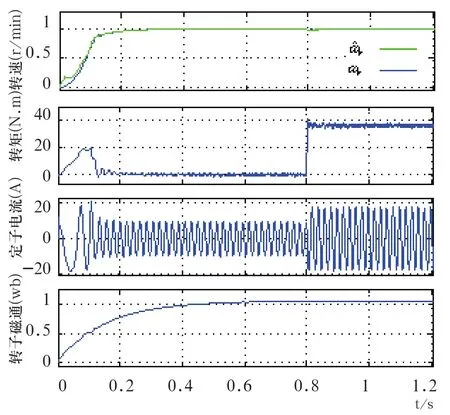
图3 空载起动和负载突变时的响应

图4 给定转速变化时的响应

0秒时转速由0突变为1460r/min，空载起动，负载在0.8秒时由0突变为额定值时的波形如图3所示。0秒时系统在给定转速730r/min、负载5N·m下起动， 0.8秒时给定转速突变为额定值时的波形如图4所示。从图3和图4中可以看出，系统在空载起动、突加负载和给定转速变化时都具有非常好的动、静态性能。

从上面两图中还可以看出，除了在起动的初始阶段，实际转速ωr和估算转速的波形几乎重合，说明文中系统所使用的转速估算方法是合理的，并且效果比较好。

为了进一步验证LADRC系统对参数变化的鲁棒性及其自适应性，图5(a)为在额定转速下空载起动，1.5秒时转子电阻值由0.507Ω突变为0.707Ω时的磁链波形，图5(b)为在额定转速下空载起动，1.5秒时转动惯量由0.01 kg·m2突变为0.05 kg·m2的磁链波形。从图中可以看出，不论是转子电阻突变或转动惯量突变，LADRC磁链都不受影响，所以认为LADRC对参数变化具有非常好的鲁棒性和自适应性。

图5 电机参数变化时的转子磁通

4 结论

本文提出一种无速度传感器矢量控制异步电机调速系统控制方案。控制器采用线性自抗扰控制器，它不需要电机的精确数学模型，通过线性扩张状态观测器估计出电机模型中的耦合项及参数摄动等引起的总扰动并加以补偿，实现了磁链和转矩的完全解耦，使系统线性化为积分器串联型结构，从而简化了控制对象，提高了控制性能。磁通观测器能准确地估计转子磁通，进而推算出转子速度，且对转子电阻固有鲁棒性。仿真结果表明整个系统具有非常好的动、静态性能，参数鲁棒性和自适应性。

[1] P.Vas.Sensorless Vector and Direct Torque Control[M].Oxford:Oxford Univ press,1998.

[2] K.Rajashekara,A.Kawamura,K.Matsuse.Sensorless Control of AC Motor Drives-Speed and Position Sensorless Operation[M].New York: IEEE Press,1996.

[3] 陈硕,Mineo Tsuji.基于磁通观测器的感应电机无速度传感器矢量控制系统[J].电工技术学报,2001,16(4):30-33.

[4] 韩京清.自抗扰控制器及其应用[J].控制与决策,1998,13(1):19-23.

[5] 冯光,黄立培,朱东起.采用自抗扰控制器的高性能异步电机调速系统[J].中国电机工程学报,2001,21(10):55-58.

[6] Z.Q.Gao,S.H.Hu,F.J.Jiang.A novel motion control design approach based on active disturbance rejection.Proceedings of IEEE Conference on Decision and Control, Dec.2001,pp.4877-4882.

[7] 刘鸣,邵诚.异步电动机的自抗扰控制器及其参数整定[J].控制与决策,2003,18(5):540-544.

[8] Liming Sun,Xuezhi Jiang,Donghai Li.Tuning of Auto-disturbance-rejection controller for a class of nonlinear plants[J].ACTA AUTOMATICA SINCA,2004,30(2):251-254.

[9] Zhiqiang Gao,Scaling and Bandwidth-Parameterization Based Controller Tuning[C].Procee dings of American Control Conference,2003,4989-4996.

TM301.2

A

1009-0134(2010)10(上)-0039-04

10.3969/j.issn.1009-0134.2010.10(上).12

2010-01-06

教育部科学技术研究重点课题资助（209004）；天津工程师范学院科研发展基金资助项目（YY09005）

刘丽英（1976 -），女，内蒙古凉城人，讲师，博士研究生，主要从事现代电力电子与电力传动及其计算机控制方面的研究。