多元线性回归预测法在服装制造中的应用

乔亮亮 (上海海事大学物流工程学院,上海200135)

根据中国服装协会对部分服装产业集群抽样调查显示,每年受到人力成本、原料成本、能源成本、政策成本上升的影响,中小企业面临生存威胁,特别是人数在100人以内的小企业关、停现象普遍。在这样的条件下,如何提高需求预测的精度是企业所面临的问题之一。在物流需求预测中,物流需求的多少受到多种因素的影响,可以通过在各相关影响因素间建立回归预测模型来实现对物流量的预测。回归就是研究自变量与因变量之间的关系的分析方法。

已知某青年女装1993～2005年13a中每个季度的销售额及其相关影响因素的数据,见文献 [1]。下面,笔者用多元线性回归法进行预测,求出其数学模型,并进行误差及精度检验。

1 估计参数

如果不能确定哪些自变量应包括在变量内,可以利用所考虑的所有变量建立一个相关矩阵[2],保留因变量与自变量高度相关的因素,而把能引起多重共线性的自变量删去或替换。

考虑年份、男女比例、购买力、人均购买数、文化程度、生产状况、人口数,销售额等因素,由文献 [1]中数据计算其相关矩阵如表1所示。

表1 相关矩阵

由表1数据可知,年份和购买力与销售额的相关系数较大,其他因素不存在多重共线问题,故选用年份和购买力为数学模型的参数,分别记做X1,X2。

2 模型建立

分别以年份和购买力为X、Y轴,销售额为Z轴绘制散点图,如图1。

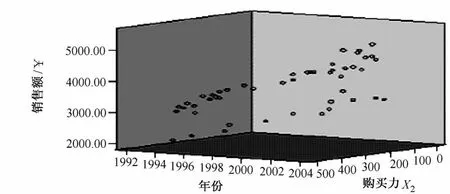
图1 相关因素的散点图

由图1可以看出,这些散点大致呈直线型,与前面假设相符,所以可将该模型设为二元线性回归[2],销售额的预测值:

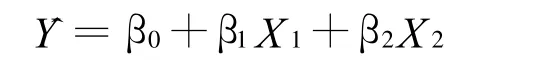
3 系数求解

回归系数的确定用自小二乘法求得。通过最小二乘法[3]可得如下方程组:

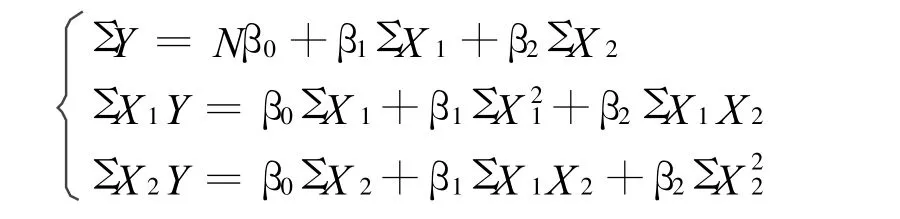
将表1中的数据带入上式中,得到:

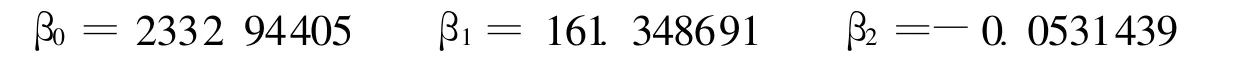
所以其数学模型为:

依据以上计算,可以得销售额的预测值,如表2所示。

4 误差及精度分析

4.1 拟合程度评价

因变量y的各个观察值点聚集在回归直线周围的紧密程度,称为回归直线对样本数据点的拟合程度[2]。通常用可决系数R2来衡量。它取值于0和1之间,并取决于回归模型所解释的y方差的百分比。可决系数R2的公式为:

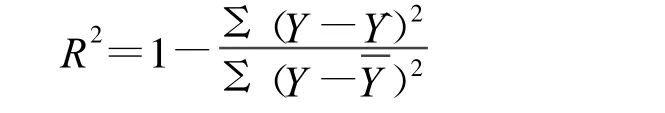
显然残差平方和占离差平方和的比重越小,可决系数R2越大,回归直线的拟合程度越强。可决系数R2的取值区间为 [0,1],实际上,可决系数R2是线性相关关系r的平方,｜R｜越接近于1,则因变量与自变量的线性相关关系越密切,回归直线拟合程度越高[3]。带入数据得:

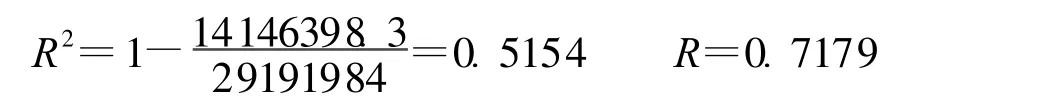
由此可以看出此回归模型解释了服装销售量变差的51.54%。

4.2 标准误差

标准误差又称剩余标准差,是评价回归直线代表性大小或实际值与估计值的标准误差大小的综合指标,也是计算置信区间估计值和其他拟合优度的基础指标。计算公式如下:

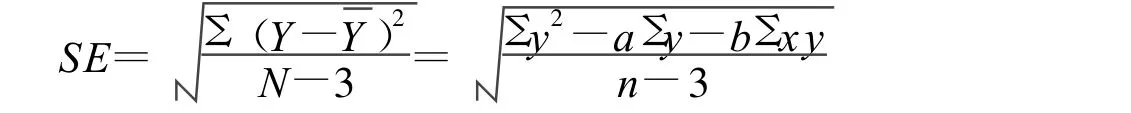
将数据带入得:

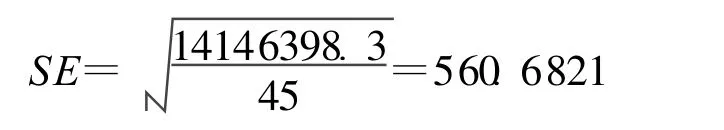
4.3 回归系数的显著性检验

回归系数的显著性检验是用t参数检验的。t服从自由度为n-3的t分布,取显著性水平α=0.05,查表得tα=2.021,若｜tβ1｜＞tα则说明回归系数显著。在该模型中:

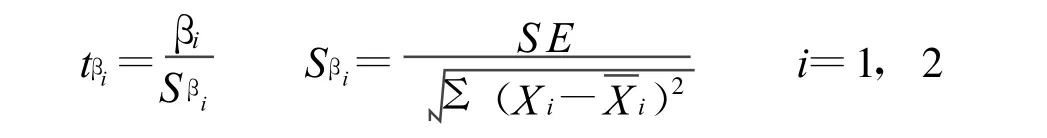
带入数据得:

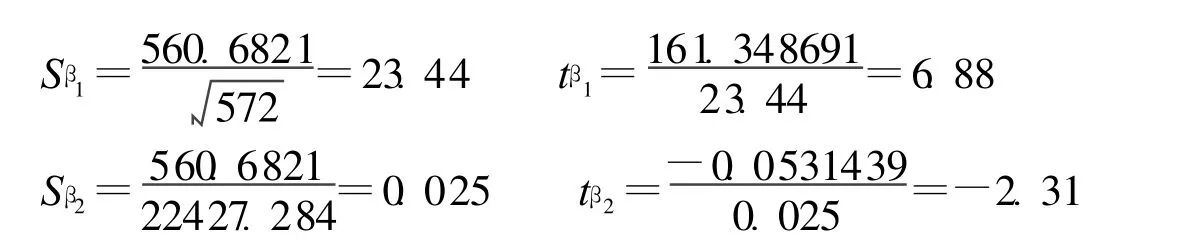
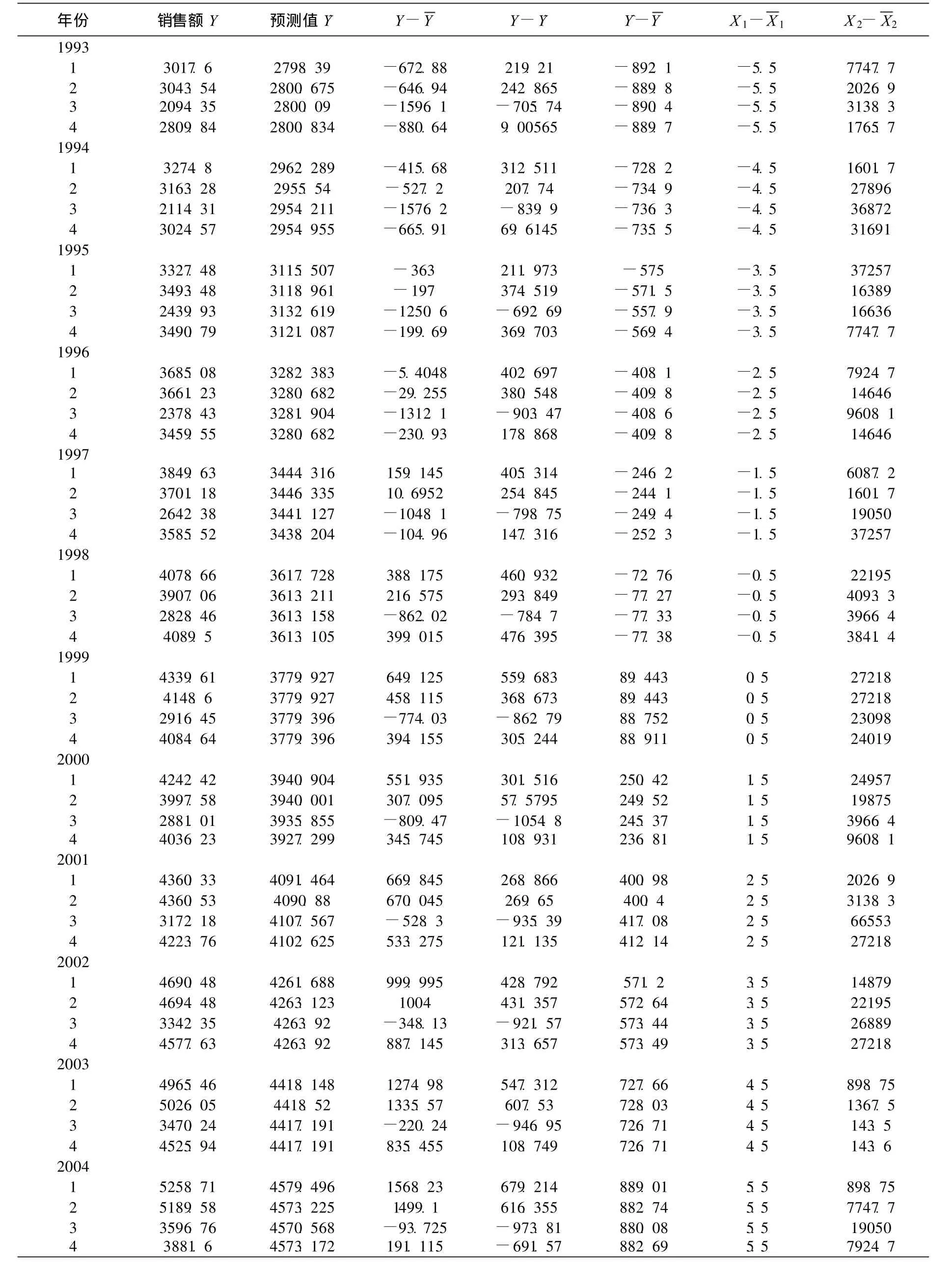
表2 预测值及其它参数

由以上的结果可以看出2个系数的｜t｜＞tα所以回归系数β1,β2显著。

4.4 回归方程的显著性检验

即检验整个回归方程是否具有显著性,判别y与x之间是否存在真实的线性相关,采用F检验[4]。其公式为:

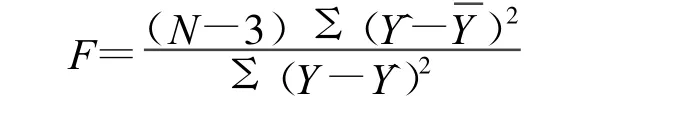
F服从F(1,n-3),取显著性水平 α,如果 F＞F(1,n-3)则表明回归模型显著,如果F＜F(1,n-3)则说明回归模型不显著,回归模型不能用于预测。

在本模型中,默认的α=0.05,n=48,查表得F(1,45)=4.08将已知数据带入得:

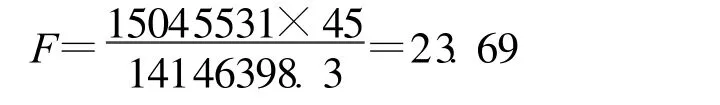
因为F＞F(1,n-3)因此回归模型显著,可用于预测。

[1]徐国祥.统计预测和决策[M].上海:上海财经大学出版社,2005.

[2]江铃.统计学 [M].北京:人民邮电出版社,2007.

[3]郑雪梅.青岛朗讯需求预测改进及应用研究 [D].北京:北京交通大学,2007.

[4]李志辉,罗平.Sp ss for Window s统计分析教程 [M].电子工业出版社,2003.