一类差分方程的振动性研究

王剑杰 (山西财经大学应用数学学院,山西 太原030006)

在科学技术和经济研究中,差分方程是一个有力的数学工具。研究差分方程可以在分析经济走势时,将突发事件的影响也考虑其中,克服了微分方程描述客观经济走势中无法计入离散情况的不利,使得离散的情况也可以进行定性的分析。下面,笔者研究了一类具有连续变量的时滞差分方程:

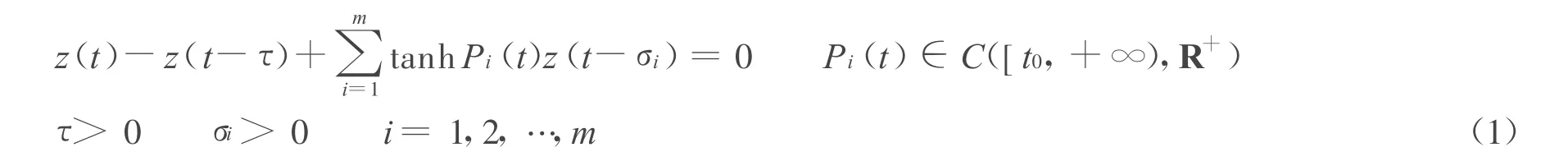
获得了方程(1)所有解振动的判据。其中,离散化部分推广了文献[1～6]中的结果。

定理 1 设 σi=kiτ+θi,θi ∈ [0,τ),ki为正整数 ,如果 :

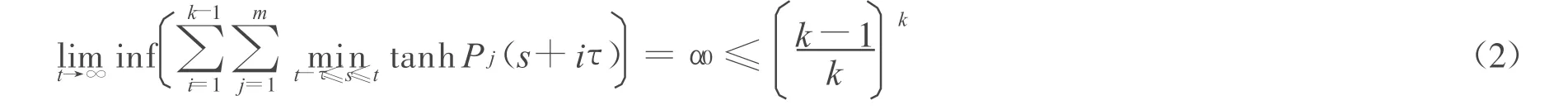
且:

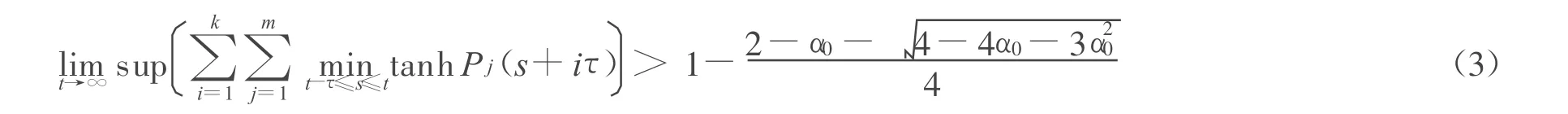
则方程(1)的每个解振动。

证明 若不然,则方程(1)有非振动解。不妨设方程(1)存在最终正解z(t)则必存在t1＞t0,使t≥t1时,z(t-σi)＞0,i=1,2,…,m,令式(1)两端从 t-τ到t积分,得:

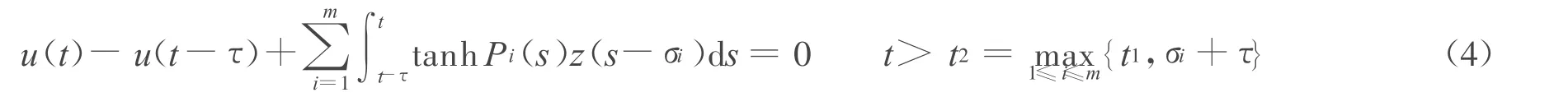
故在[t-τ,t]上tanh Pi(s)有最小值又由u′(t)≤0知u(t)单调不增,从而有u(t-σi)≥u(t-kiτ),则:

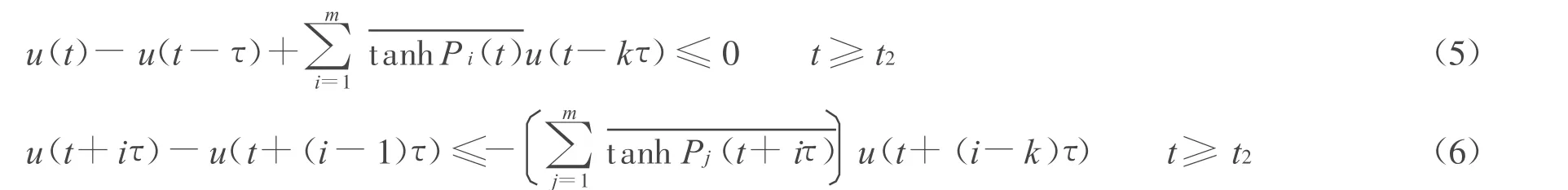
由条件(2)知存在一个充分小的ε∈(0,α0)和充分大的t,使得tanh Pj(s+iτ)≥α0-ε=α。故对任意的正整数n,则当t≥t2时,有。从而对某个t≥t2,必存在一个正整数nt∈ [n-k+2,n],使:

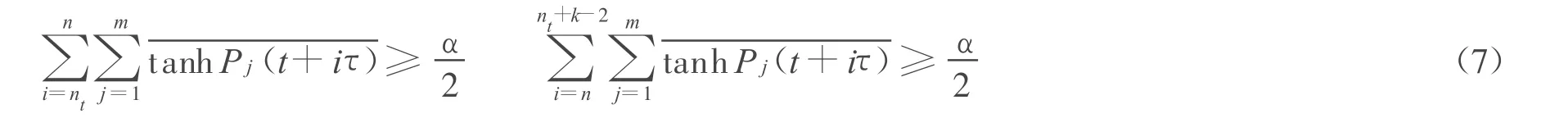
将式(6)分别从 nt到n,和 n到nt+k-2求和,再利用:

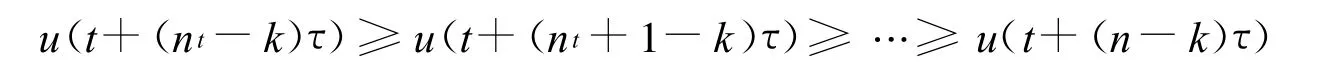
和式(7)可得到:

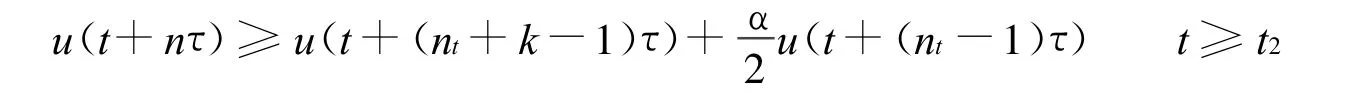
定义正实数序列{βm}:

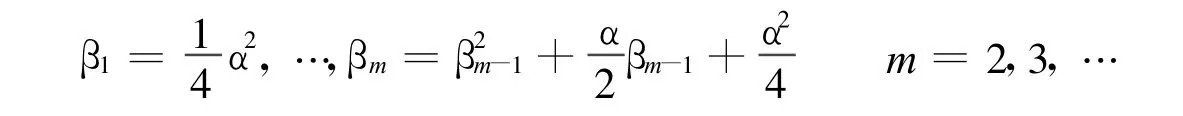
由文献[3]知:

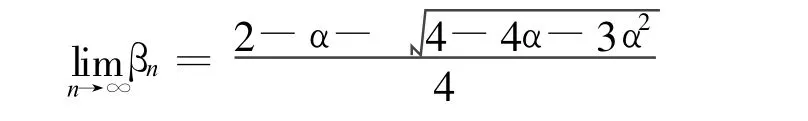
故有:

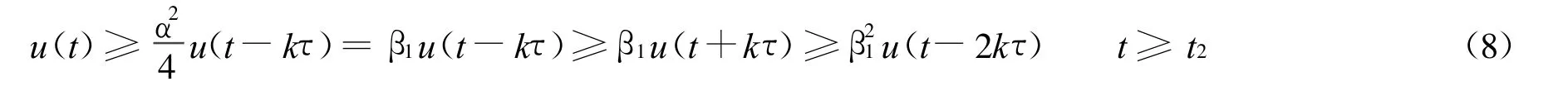
由n-k+2≤nt≤n,有:

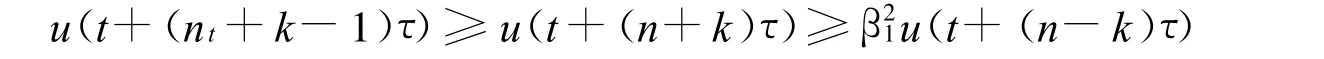
结合式(8)得:

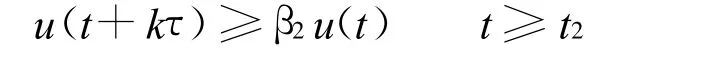
重复上面的步骤,有:

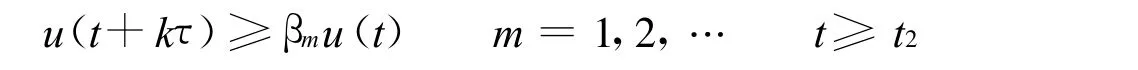
对式(6)两边从1到k求和,并利用u(t+(1-k)τ)≥u(t+(2-k)τ)≥… ≥u(t),可得到:

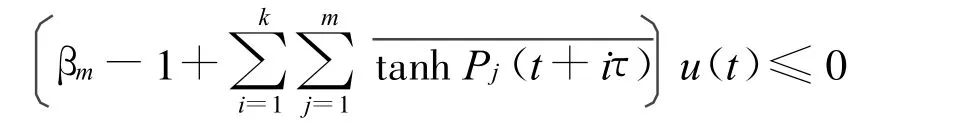
又u(t)＞0,故:

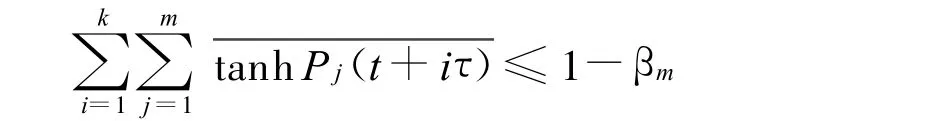
令m →∞,t→∞,又ε→0时,α→α0,则有:

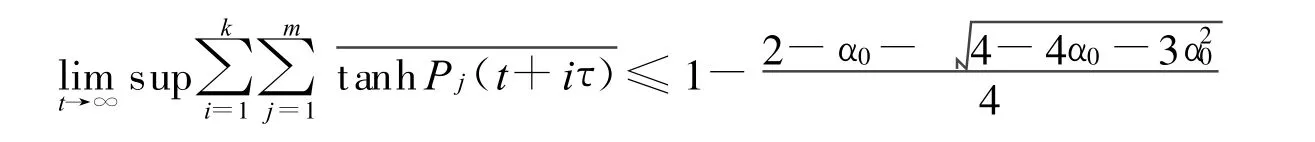
这与条件(3)矛盾,定理1得证。

[1]张玉珠,燕居让.具有连续变量的差分方程振动性的判据 [J].数学学报,1995,38(3):406～411.

[2]周 勇.具有连续变量的变系数差分方程的振动性 [J].经济数学,1996,13(1):86～89.

[3]戴斌祥.具有连续变量的差分方程的振动性 [J].经济数学,1997,14(1):64～68.

[4]张友生,庾建设.具连续变量的线性时滞差分方程的振动性[J].高校应用学报A辑,2000,15(1):25～33.

[5]Zhang BG.Oscillations of a class of difference equations w ith continuous argumen ts[J].Applied M athematics Letters,2001,14:557～561.

[6]Shen Jianhua,Tang Xianhua.New nonoscillation criteria for delay differential equations[J].Journal of Mathematical Analysis and Applications,2004,290:1～9.