快速计算一维分层粗糙面之间金属目标复合散射的互耦迭代算法

姬伟杰 童创明②

①(空军工程大学导弹学院 三原 713800)

②(毫米波国家重点实验室 南京 210096)

1 引言

粗糙面和目标的复合散射在雷达探测、目标识别和远程遥感等领域有着重要的应用。近年来，计算粗糙面和目标的混合场的数值解法引起了诸多学者的兴趣。例如：Johnson[1]曾用“四路径”模型计算无限大介质平板上介质目标的散射，文献[2]利用GFBM/SAA研究低掠角入射时动态分形粗糙面和2维舰船目标的双站散射模拟， 文献[3,4]利用互耦迭代方法计算了金属粗糙面与上方目标的差场散射，文献[5]等用矩量法计算了粗糙面与上方或下方目标的复合散射，文献[6]等基于互易定理和矩量法研究了平面上方2维介质目标对高斯波束的电磁散射，文献[7]等研究了粗糙海面上方金属目标复合散射的解析-数值混合算法。

在实际自然界中，分层媒质粗糙面更具有实际意义，比如覆盖植被或雪的地面。可能由于计算量过于庞大，大多数学者都研究单层粗糙面和目标的复合散射，只有少数学者研究了更具有实际意义的分层粗糙面和目标复合散射。例如：文献[8]研究了双层随机粗糙面和地下目标的复合散射。文献[9]研究了分界面是平面的分层媒质上方目标的散射。文献[10]用FDTD研究了双层粗糙面上方金属目标的散射，文献[11]中用EBCM计算了分层粗糙面和下方目标的复合散射，但是该算法只限于计算微粗糙面和小目标的复合散射(例如半径为0.16λ的圆柱)，不能计算中等程度粗糙面与较大目标的复合散射。

由于不受粗糙面参数和目标尺寸的限制，因此，数值算法的研究显得更有意义。以前的研究都将目标和分层粗糙面一起看成一个组合散射体，电磁积分方程离散后产生了巨大的未知量，需要庞大的计算量和存储量，对计算机硬件和程序员编程技巧提出了很高的要求，这在很大程度上限制了数值算法的应用。

在分层粗糙面与目标的复合散射计算中，粗糙面的未知量占绝大多数，而目标的未知量只占一小部分。因此如何有效计算粗糙面的电磁散射是一个很重要的问题。近年来发展的前后向迭代法(FBM)[12]对粗糙面这类散射问题有很好的收敛性，在文献[13]中，Moss C D等人进一步将其与谱加速(SAA)结合并应用于计算分层粗糙面的电磁散射特性。本文结合FBM和Bi-CG，基于物理散射机理，提出一种计算双层介质粗糙面及下方金属目标复合电磁散射的快速互耦迭代数值算法(CCIA)。建立了目标与分层粗糙面的耦合积分方程，将其分解为含有两个方程的方程组，对分层粗糙面的散射方程用FBM求解，目标的散射方程用双共轭梯度法(Bi-CG)[14]求解，粗糙面与目标的耦合作用通过更新两方程的激励项来实现，每次迭代过程中，粗糙面的激励项中不仅有锥形入射波还有目标对其的散射波；同样，目标的激励项中也包括上层粗糙面的透射波和下层粗糙面的反射波。由于FBM和Bi-CG的计算量均为O(N2)，因此该算法的计算量为O(N2)，而传统的矩量法(如高斯消元法)的计算量为O(N3)，因此计算效率大大提高。经过计算，该算法具有良好的收敛性，当目标趋于无穷小时复合散射系数与只有分层粗糙面时的散射系数相吻合，验证了算法的有效性。最后，讨论了目标尺寸与深度变化对复合散射系数的影响。

2 基本理论

2.1 电场积分方程(EFIE)

设无限长金属圆柱目标位于双层粗糙面中间，如图1所示。ψin为入射场，ψl为区域l中的场(l=0,1,2)。当入射波为TE和TM波时，ψ分别表示电场和磁场(本文只考虑TE波入射)，在各区域中应用格林定理：

n表示分界面表面法向向量。边界条件为

2.2 耦合积分方程组

设粗糙面长度为L，离散密度Δx，离散总数为N，粗糙面Sl的高度用fl(xn)来表示。目标表面用Δx0均匀离散，离散总数为M，目标表面用z0(xn)表示。结合边界条件，式(1)-式(3)整理为

整理式(4)便可得到分层粗糙面与下方金属目标耦合矩阵方程组：

其中式(5a)是求解分层粗糙面表面电流的方程，而式(5b)则是求解目标表面电流的方程。该方程组表明粗糙面不仅受到初始入射波的影响，同时还要受到目标对其散射的影响，目标则只受到分层粗糙面对其散射的影响。=Cl⋅U，表示目标对第l个0分界面的散射。ψSur=E(l)⋅Ul+F(l)⋅ψl，表示上层分界面的透射波与下层分界面反射波之和。

2.3 用CCIA求解耦合积分方程组

式(5)若直接用传统矩量法求解则计算量为O(N3)，需要耗费大量的时间。这里介绍一种新的迭代算法来快速求解该方程组，其中第i步的迭代方程如下：

其中Z0和Z1分别为分层粗糙面与目标的阻抗矩阵，V0(i)表示第i次迭代过程中粗糙面的总入射波，包括锥形入射波和目标对粗糙面的散射波。V1(i)表示第i次迭代过程中目标总的入射波，包括上层粗糙面的透射波与下层粗糙面的反射波。

对式(6a)，采用FBM求解，将各子矩阵分解为上、下和对角矩阵，分别用U、D和L表示。例如，对上标为(l, l, l)的子矩阵有

将未知向量分解为前后向分量，Ul=+，ψl=+，这里，和是前向分量，和是后向分量。于是，式(6a)中前向电流迭代公式写为

类似地可得到后向电流的迭代公式。由迭代求解，第i次迭代的未知量为迭代算法以=0，=0，=0，=0为初始值，迭代至指定收敛精度。

用Bi-CG解式(6b)，FBM和Bi-CG求解均为循环迭代过程，称为内循环，设其各自的收敛精度为γ=10−4。而式(6a)和式(6b)的互耦迭代过程称为外循环。由于FBM的计算量为O()(NSur为粗糙面的未知量个数)，Bi-CG的计算量为O()(NTar为目标的未知量个数)，外循环迭代一次计算量为O()(N为总的未知量个数)，因此该算法总Total的计算量为O()，较之传统矩量法O()计算效率大为提高。

定义第n步外循环迭代误差为

其中Ztotal和Itotal分别表示分层粗糙面与目标总的阻抗矩阵和表面电流向量。从Itotal(n)=0开始迭代计算，此时粗糙面的入射波只有锥形波。计算得到粗糙面的表面电流分布，代入式(6b)右端激励项计算目标的总激励，此时目标的入射波包括上层粗糙面的透射波和下层粗糙面对反射波。计算得到目标的表面电流再代入式(6a)右端更新粗糙面的激励，如此反复迭代直至达到指定收敛精度。

2.4 锥形入射波和双站散射系数

为减小人为截断引起的误差，采用Thorsos锥形波，表达式为[15]

其中θi为入射角(相对于z轴逆时针方向)，k表示上半空间的波数，g是波束宽度。

定义双站散射系数[5]为

其中θ为散射角，ψs(θo, θi)为散射场。

3 数值计算和讨论

本文中所有分界面均采用高斯粗糙面，长度为L，相关长度为li(i=1,2)，均方根高度为hi(i=1,2)，i=1,2分别表示上层和下层分界面，计算过程中应避免上层分界面与下层分界面相重叠，金属目标位于两层粗糙面之间。媒质的相对介电常数为εr1，εr2，上层介质厚度为d。求解时采用脉冲基函数离散粗糙面表面电流分布，剖分单元为Δx=λ/10，圆柱半径为R，深度dp为目标与上层粗糙面的距离，xp为目标中心的水平位置，剖分单元总数为120。如无特殊说明，文中参数的设置如下：εr1=4.0+0.01i ，εr2=7.0，d=6.0λ，R=1.0λ，dp=2.0λ，xp=0.0λ，θi=30o，g=L/4 ，L=40λ，h1=h2=0.1λ，l1=l2=1.0λ，文中所有结果均是对50个样本取均值得到的。所用计算机配置为：主频：1.65 GHz ，内存：1 GB。

算法有效性的验证。令目标尺寸趋于零，比较此时的散射系数与由矩量法得到的相同介质参数、粗糙度参数对应的分层粗糙面(粗糙面之间无目标)电磁散射系数的差异即可验证该算法的有效性。图2所示为圆柱目标半径退化10−4λ时的散射系数与只有粗糙面时的散射系数相比较。 由图可知，目标尺寸趋于零时的散射系数与无目标时的结果吻合得很好，验证了算法的有效性。

算法的计算精度与收敛性。其它参数不变，令上下层分界面均方根高度分别取0.1 λ，0.3 λ，0.5 λ。图3 给出了外循环迭代误差τ随迭代步数的变化关系。图中还给出了当目标边长为a=1.0λ的无限长立方柱，上下层分界面均方根高度为0.1 λ时的情况。 由图可知，对不同粗糙度的粗糙面，经过15步迭代，外循环收敛精度都能达到10−5以下，远远满足计算精度要求。经过验证，通常收敛精度为τ=10−2即可满足精度要求，因此经过4步迭代即可终止，并且不论是圆柱目标还是立方柱目标该算法都具有良好的收敛性，同时由图可知，由于立方柱周长小于圆柱周长，对于相同参数的粗糙面，目标为方柱时的收敛性较好。

图4 给出了内循环FBM的迭代次数随外循环迭代步数的关系，由图可知，经过4步外循环之后，FBM只需迭代1次即可收敛，具有很好的收敛速度。由于计算分层粗糙面与目标复合电磁散射过程中，计算分层粗糙面表面电流占用了大量时间，因此FBM迭代次数的减少大大节省了时间，提高了计算效率。值得指出的是，当目标为圆柱，h1=h2=0.1λ，收敛精度取τ=10−2时，用互耦迭代算法实现一次需要240 s，而用传统高斯消元法需要485 s，节省了约一半时间，实现50次可节省3个多小时，较传统矩量法计算速度大为提高。

图5给出了分层粗糙面中间存在无限长金属圆柱和立方柱时的散射系数，其中立方柱边长为a=1.0λ，圆柱半径为1.0 λ。图中还给出了只有分层粗糙面时的散射系数，由图可知，当粗糙面中间存在目标时，后向散射方向散射系数明显增大，而前向散射方向散射系数有所减小，并且当目标为圆柱时变化更为明显，这是因为圆柱目标的周长比立方柱稍大(2πR＞4a)，所以圆柱与分层粗糙面的作用更加明显。因此，当分层粗糙面中间存在目标时，由于目标与粗糙面之间的相互耦合作用，散射系数明显发生改变，当计算目标与环境的相关问题时，必须考虑两者之间的相互作用。

图2 算法验证

图3 τ随迭代步数的变化关系

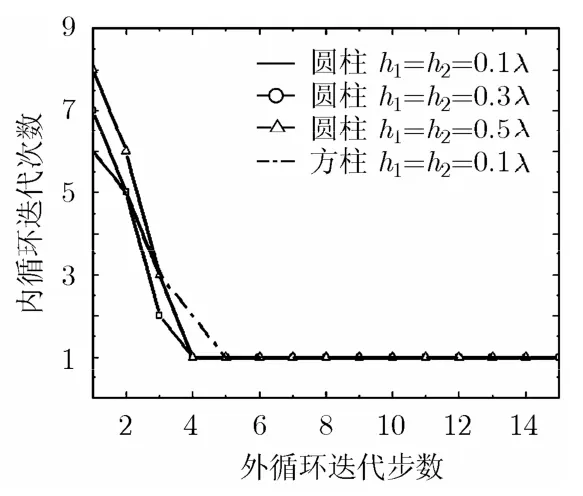
图4 内循环迭代次数

讨论圆柱目标大小对散射系数的影响。令其他参数不变，目标半径取0.5 λ，1.0 λ，1.5 λ，收敛精度取τ=10−2。双站散射系数见图6，由图可知，随着圆柱目标半径的增大，目标与分层粗糙面的相互作用增强，复合散射系数增大，尤其在镜面反射方向附近以外的很大范围内这一结论表现的尤为明显。可见圆柱目标的半径大小对复合双站散射系数有明显影响，同时也验证了该算法对不同尺寸目标均具有良好的收敛性。

图7给出了当R=1.0λ时，由文献[4]中方法计算的单层粗糙面下方金属圆柱目标复合散射系数与分层粗糙面之间金属圆柱目标复合散射系数的对比结果。由图可知，与单层粗糙面相比较，由于存在下层粗糙面与上层粗糙面的相互作用，以及下层粗糙面与目标的相互作用，使得复合散射系数增大，尤其在镜面反射方向附近范围内变化更为明显。

图5 有无目标时分层粗糙面的散射系数

图6 不同尺寸目标对应的散射系数

图7 与单层粗糙面结果对比

讨论目标位置对散射系数的影响。其余参数不变，目标深度取1.5 λ，2.0 λ和2.5 λ收敛精度取τ=10−2。相应的散射系数如图8所示，图中还给出了目标深度取1.5λ，2.0λ时单层粗糙面下方金属圆柱目标的散射结果。由图可知，当目标深度增大时，分层粗糙面与下方目标的复合散射系数变化不明显，而单层面与下方目标的散射系数明显减小。这是由于对于双层粗糙面，当目标深度增加时，目标与上层粗糙面的距离增大，相互作用减小，但与下层粗糙面的却又距离减小，相互作用增大，因此目标与分层粗糙面的相互作用变化不是特别明显。

4 结论

图8 不同目标深度对应的散射系数

用基于FBM和Bi-CG的互耦迭代算法(CCIA)快速获取了1维分层媒质粗糙面之间无限长金属圆柱目标和无限长立方柱目标的复合电磁散射特性，并对计算结果进行了验证，讨论了算法的收敛性，当目标周长较小时，算法具有更好的收敛速度。计算了不同目标尺寸对应的复合散射系数，结果表明，随着目标尺寸的增大，分层粗糙面与目标的相互耦合作用增强，散射系数增大，反之则减小。将计算结果与单层粗糙面下方金属目标结果相比较。结果表明，由于下层粗糙面与上层粗糙面以及目标的相互作用，散射系数明显增大。同时，讨论了目标深度变化对复合散射系数的影响，结果表明，当目标深度变化时，分层粗糙面与下方目标的复合散射系数变化不明显。

[1] Johnson J T. A study of the four-path model for scattering form an object above a halfspace[J]. Microwave Optical Technology Letters, 2001, 30(2): 130-134.

[2] Jin Y Q and Li Z. Simulation of scattering form complex rough surface at low grazing angle GFBM/SAA method [J].IEEE Transactions on Fundamentals and Materials Society(A), 2001, 121(10): 917-921.

[3] Ye Hong-xia and Jin Ya-qiu. Fast iterative approach to difference scattering from the target above a rough surface[J].IEEE Transactions on Geoscience and Remote Sensing, 2006,44(1): 108-115.

[4] Ye Hong-xia and Jin Ya-qiu. A hybrid analytical-numerical algorithm for scattering froma3-D target above a randomly rough surface[J]. Acta Physica Sinica, 2008, 57(2): 839-846.

[5] Wang X, Wang C F, and Gan Y B. Electromagnetic scattering from a circular target above or below rough surface[J]. Progress in Electromagnetics Research, 2003, 40:207-227.

[6] Wang Yun-hua, Zhang Yan-min, and Guo Li-xin.Investigation of the scattered field form a two-dimensional dielectric target above the planar surface with a Guass beam incidence[J]. Acta Physica Sinica, 2008, 57(9): 5529-5535.

[7] Wang Rui, Guo Li-xin, Qin San-tuan, and Wu Zhen-sen.Hybrid method for investigation of electromagnetic scattering interaction between the conducting target and rough sea surface[J]. Acta Physica Sinica. 2008, 57(6):3473-3480.

[8] Magda El-Shenawee. Polarimetric scattering from twolayered two dimensional random rough surfaces with and without buried objects[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(1): 67-76.

[9] Chew W C, Jin J M, Michielssen E, and Song J M. Fast and Efficient Algorithms in Computational Electromagnetics[M].Norwood: Artech House Publishers, 2001: 40-65.

[10] Li J, Guo L X, and Zeng H. FDTD Investigation on Electromagnetic Scattering form the PEC Cylinder above Two_Layered Rough Surfaces[C]. ICMMT, Nanjing 2008:531-534.

[11] Kuo Chih-hao and Moghaddam M. Electromagnetic scattering from a buried cylinder in layered media with rough interfaces[J]. IEEE Transactions on Antennas and Propagation, 2006, 54(8): 2392-2401.

[12] Holliday D, DeRaad L L, and StCyrGJ. Forward backward:a new method for computing low-grazing angle scattering[J] .IEEE Transactions on Antennas Propagation, 1996, 44(5):722-729.

[13] Moss C D, Grzegorczyk T M, Han H C, and Kong J A.Forward-backward method with spectral acceleration for scattering from layered rough surfaces[J]. IEEE Transactions on Antennas and Propagation, 2006, 54(3): 1006-1016.

[14] Lin J H and Chew W C. BiCG-FFT T-Matrix method for solving for the scattering solution from inhomogeneous bodies[J]. IEEE Transactions on Microwave Theory and Techniques, 1996, 44(7): 1150-1155.

[15] Thorsos A. The validity of the Kirchhoff approximation for toygh surface scattering using a Guassian roughness spectrum[J]. Journal of the Acoustical Society of America,1988, 83(1): 78-92.