一种新的单站红外目标纯方位参数航迹滤波方法

刘进忙 姬红兵 樊振华 张张珣

①(西安电子科技大学电子工程学院 西安 710071)②(空军工程大学导弹学院 三原 713800)

1 引言

本文作者总结出分坐标处理目标信息的思想，可利用静止单站红外传感器所得到目标的纯方位、纯仰角信息分别建立目标的参数航迹，实现目标航迹滤波和目标跟踪。文献[7]提出了余切关系定理，利用方位序列仅提取目标的航向角不变量，实现了单站航向角的估计及两站目标其它航迹参数的解算与目标跟踪。文献[8]总结了静止单站的目标方位序列的拟线性估计算法(PLE)和使用辅助变量的目标定位算法(INVPLE)。本文提出纯方位参数航迹模型建立与滤波算法，较好地解决了红外单站的目标参数航迹跟踪问题。

2 直线运动目标的航迹参数计算原理

2.1 匀速直线运动目标的航迹参数滤波

匀速直线运动目标航迹在平面直角坐标中的示意图如图1所示。观测站在O点，设目标沿直线l做匀速直线运动，目标航向角为α0，在t时刻的观测目标的方位角为βt，该点与航迹的垂足点距离为V(t−t⊥)，其中V为目标在平面的速度值，则目标的运动方程为

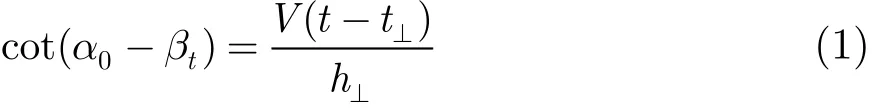
红外观测模型：

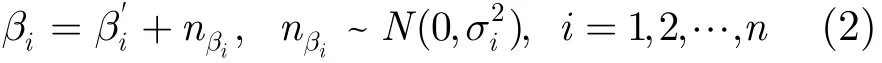
考虑观测站到目标航线上各个点坐标对测量误差影响的大小不同，根据方位误差在航迹直线上几何投影关系，设置误差加权值，当测量方差相同时==…==σ2，可构造出参量加权最小二乘目标函数为

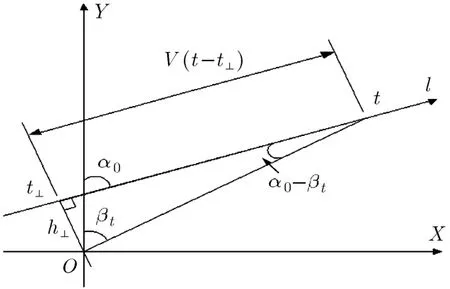
图1 目标匀速直线运动水平面示意图

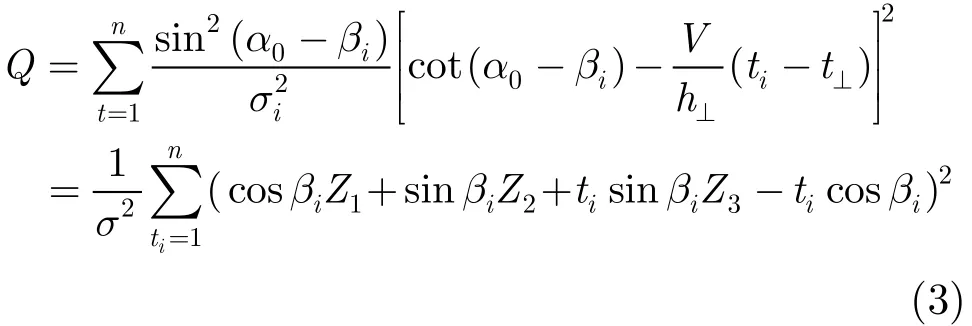
其中Z1=t⊥+(h⊥/V)cot α0，Z2=(h⊥/V)−t⊥cot α0，Z3=cot α0。而h⊥/V, t⊥,cot α0为匀速直线运动目标的航迹参数，Z1, Z2, Z3为匀速直线运动目标的航迹计算参数，前两项的物理意义是目标沿航迹过Y，X坐标轴的交点时刻的参数值。

使该目标函数Q达到最小值，可对Z1, Z2, Z3求偏导数并令为零，可得方程：

3.坚定不移地狠抓动物调运监管，确保有效防堵“外疫”入侵。规范调运动物备案准入管理，严把调运前备案审批、指定道口准入和引入后隔离检疫监管“三道关”，有效防止了外疫传入。近3年共备案从区外调入屠宰动物1 500批次，非屠宰动物130批次，区外引种审批23批次，引种8 230头，未发生审批不当引发重大动物疫情。加强了大有周边道路防疫检查消毒综合检查站容站貌、各项制度和标准化服务窗口的建设，配备了4名专职执法人员和必要的设施设备，坚持24小时值班制度，日均检查和消毒运输动物车厢15车次以上，2010年至2012年，成功拦截并无害化处理从外省入渝染疫动物3车次72头。

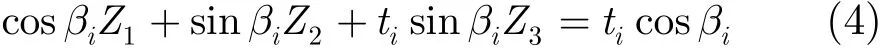
当分别在t1,t2,…,tn时刻采样方位序列时，则有矩阵形式：

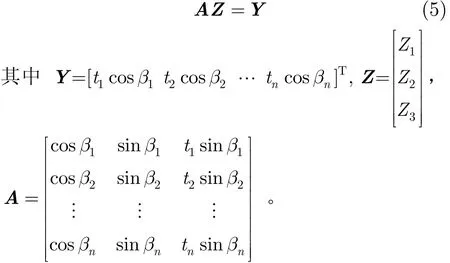
由于观测噪声nβi的影响，只能得到包含噪声成分的矩阵A和Y。利用总体最小二乘(TLS, Total Least Squares)方法[8]求解方程，较最小二乘方法更为合理、有效。目标航迹计算参数：

式中v为对增广矩阵[−Y A]进行奇异值分解后，最小奇异值所对应的右奇异向量，v(i)为向量v中的第i个元素。可解出目标的航迹参数值：

在纯方位观测条件下，单站可求解得到的目标参数航迹值：cotα0,h⊥/V ,t⊥。具体的h⊥,V值不能由单站解算得到，需多站航迹参数融合求解。

利用t1,t2,…,tn时刻计算得出的航迹参数，可预测出tn+1时刻目标的观测方位角。

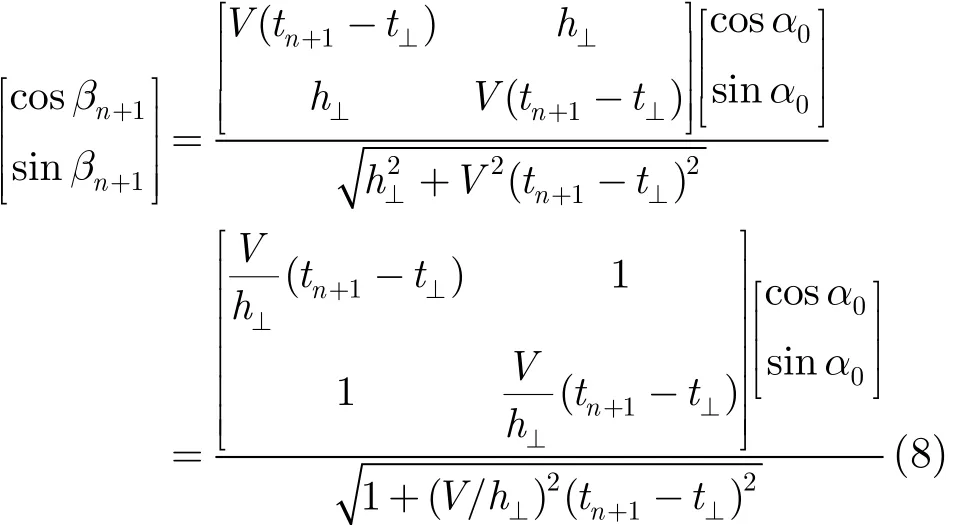
2.2 匀加速直线运动目标的参数航迹滤波

匀加速直线运动航迹在平面直角坐标中的示意图如图2所示。观测站在O点，设目标沿直线l做匀加速直线运动，目标航向角为α0，在t0时刻的观测方位角为β0，t时刻的观测方位角为βt，两点的距离为V(t−t0)+(a/2)(t−t0)2，其中V,a分别为在t0时刻的速度、加速度，则有目标位置计算公式为

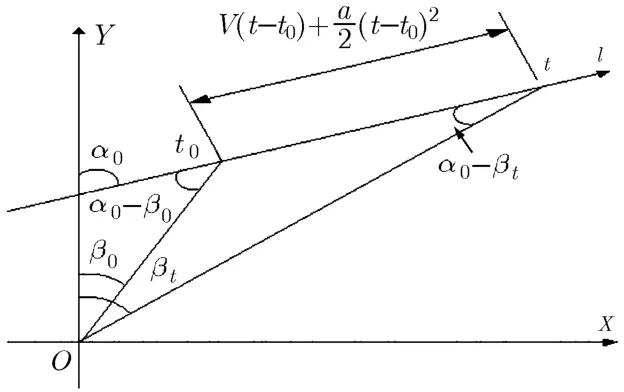
图2 目标匀加速直线运动水平面示意图

其原理类同匀速直线情况，采用加权来处理各测量时刻，构造参量加权最小二乘目标函数为

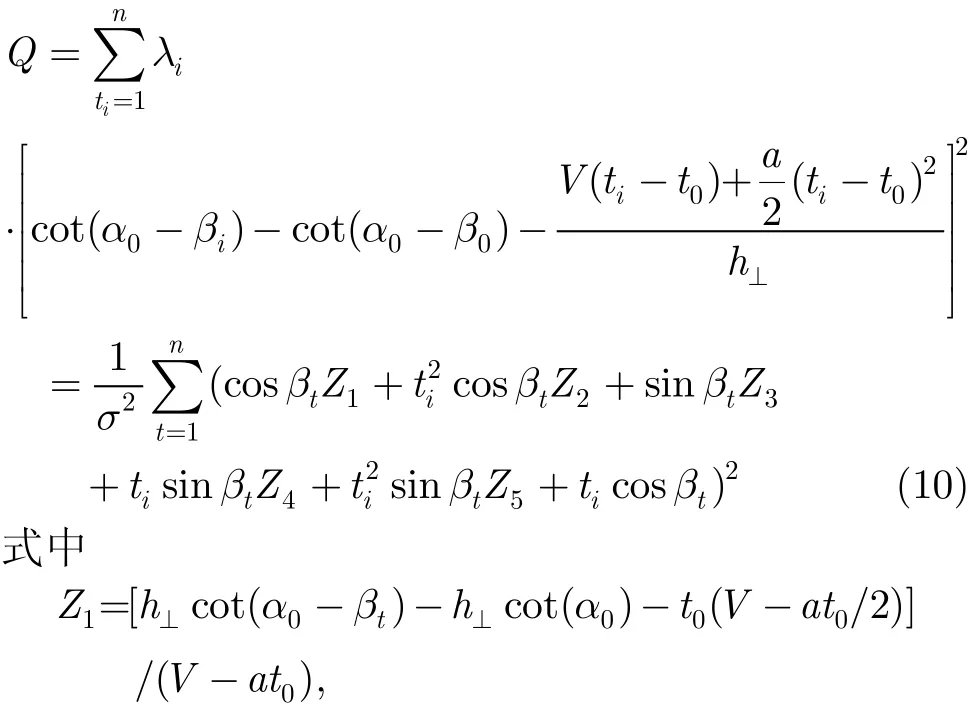
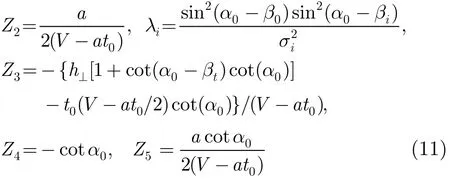
为使该目标函数Q达到最小值，可对Z1, Z2,Z3,Z4,Z5求偏导数并令为零，可得方程

故有以下矩阵形式：

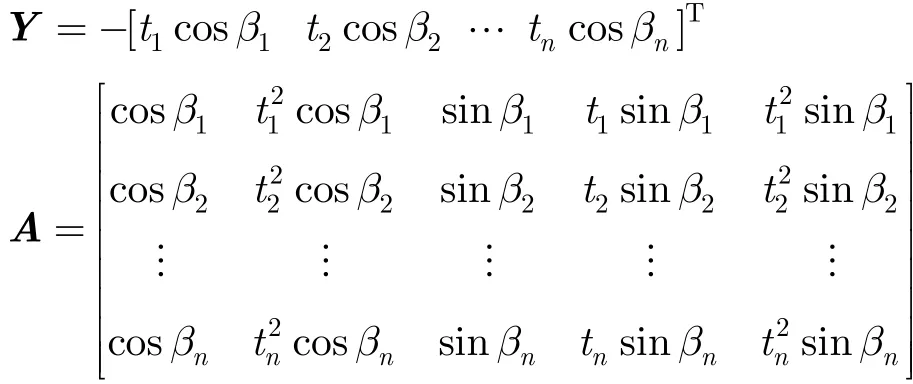
求解该方程组，同样使用总体最小二乘(TLS)方法[7]，在此不再赘述。

3 直线运动目标的参数航迹滤波仿真

3.1 匀速直线运动目标的参数航迹滤波仿真

仿真环境：采样周期T =0.05 s，即每秒钟采样20帧，相邻两帧的时间间隔为0.05 s ，仿真场景中的观测噪声nβt～N (0,)，σt=0.001。以下均采用相同的仿真环境。目标初始状态 X(1)=[x(1) vx(1)y(1) vy(1)]=[-2000,100,1000,1000] ，航向角α0=0.0997 rad。滤波窗设为 W=30,40。结果如图3所示。

仿真结果分析：由图3可知，滤波窗宽度W=40的滤波效果明显优于W=30的仿真结果。为达到更好的滤波效果，可总结如下：

(1)当选择较大窗时，对噪声的抑制作用较强，估计相对平稳，更接近真实值。但增加了计算量，将导致对曲线运动的估计存在较大的滞后。

(2)通过调整部分参数再进行实验，比较其结果说明，在80T以后，误差曲线有一些较大的波动，这是由于采用窗的长度、目标远离航迹垂直点引起非线性计算误差增大所致。可以通过适当地增加窗的长度进行有效抑制。

3.2 采用匀速直线模型对分段机动目标进行滤波

由于红外观测站的采样率较高，在较短的时间间隔内目标运动距离也相对较短，可近似用直线运动来处理，从而机动曲线运动轨迹可分段用2.1节推导出的匀速直线运动滤波算法分段逼近。

(1)对匀速转弯机动目标的参数航迹滤波

初始状态X(1)=[x(1)vx(1)ax(1)y(1)vy(1)ay(1)]=[-1000,0,40,100,200,0]，航向角α0初始值为0 rad，将随时间呈线性变化，线速度 V=200 m/s ，转弯半径 r=1000 m。滤波窗W=24,30。

仿真结果如图4所示，滤波窗宽度W=40的滤波效果明显优于W=30的仿真结果，且均方误差较小，在可接受范围内。

(2)对分段变加速机动目标的参数航迹滤波

初始状态X(1)=[x(1)vx(1)ax(1)y(1)vy(1)ay(1)]=[-200,5,60,200,300,10]，在 t=30 帧时，加速度突变为[0, -80] m2/s，并一直持续至仿真结束，航向角α0初始值为0.0167 rad将随时间呈非线性变化。滤波窗 W=30,40。

仿真结果如图5所示，滤波窗宽度W=40的滤波效果明显优于W=30的仿真结果，均方误差在机动目标快速转弯的时间段80～120帧(0.05 s)范围内有所增大，未丢失目标。在目标转弯后，均方误差又迅速减小，仍有效跟踪机动目标。

4 静止单站纯方位的其它方法仿真比较

经典的纯方位角目标分析算法[8]有PLE，IVPLE算法。PLE算法引入伪测量，将方位测量方程转化为具有线性形式的伪测量方程，直接利用几何图形推导出齐次方程求解。

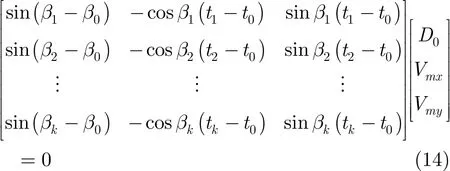
可计算得到目标航向角和其它参数。而本文算法直接利用式(7)得到航迹参数。两种算法都可以得到目标航向这几个重要参数。在相同的实验条件下，将本文算法与PLE算法性能相比较，如图6所示，本文算法的目标航向角的精度略高。

IVPLE算法可消除PLE算法的有偏性，采用辅助变量方法取得较好的效果。其思路是用解算参数来预测目标的方位，替代观测矩阵中的测量方位，试图形成与等效测量误差在统计上的解耦。在相同的实验条件下，将本文算法与IVPLE算法对目标航行角估计性能相比较，如图7所示，可看出本文算法的目标航向角的精度略高。

5 结论

本文提出直接采用方位坐标处理，从几何模型出发推导出匀速直线滤波模型，用一组航迹参数代替了目标的速度、加速度，以表征目标的运动特性，可实现目标参数航迹的滤波与跟踪。该方法为多传感器实现参数航迹融合奠定良好的基础，对校正传感器的系统误差有重要的作用，其物理意义明确，计算简单、实用，思路新颖，使得传感器组网更加灵活、简便。

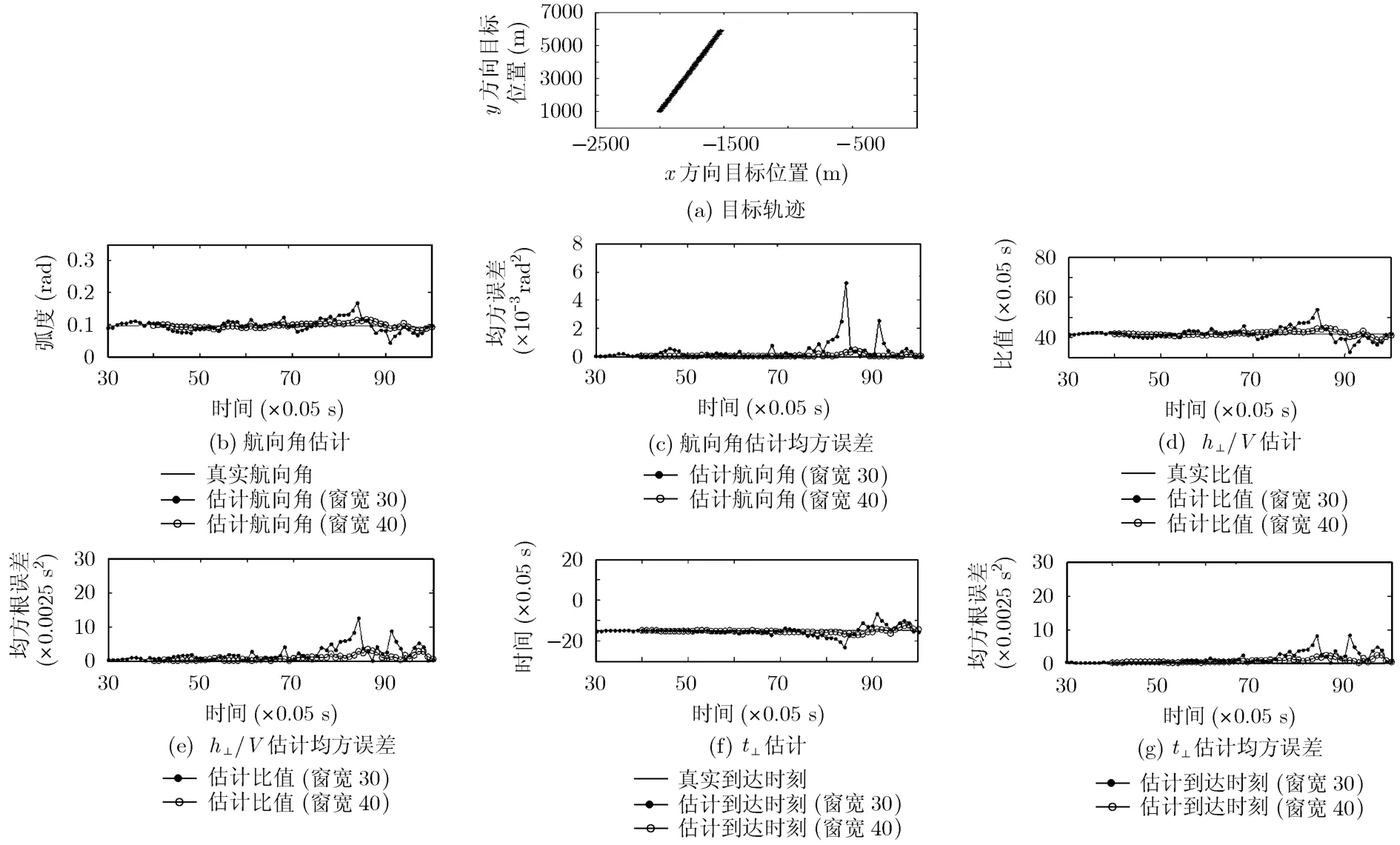
图3 匀速直线运动仿真结果

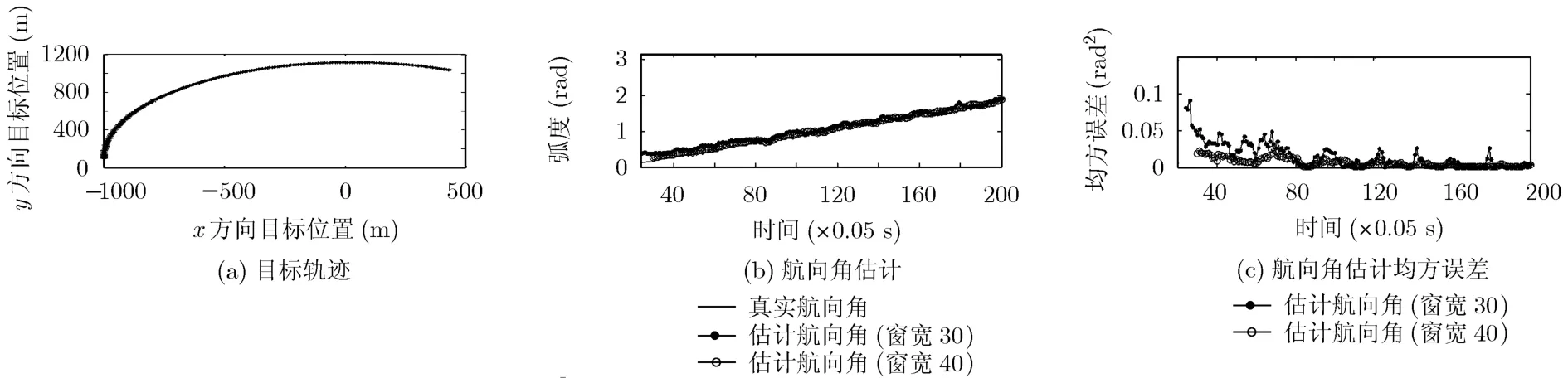
图4 对匀速转弯机动目标参数航迹滤波的仿真结果

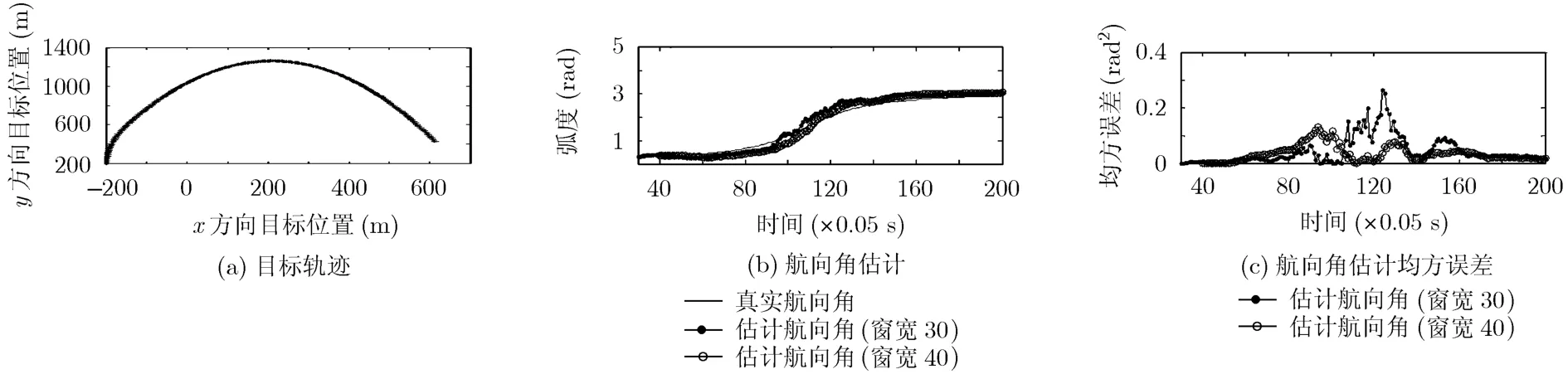
图5 对分段变加速机动目标参数航迹滤波的仿真结果

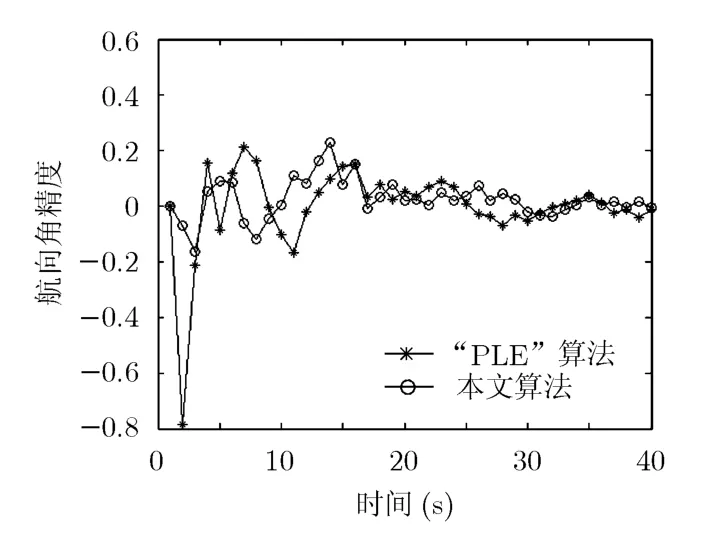
图6 与PLE算法目标航向角精度比较

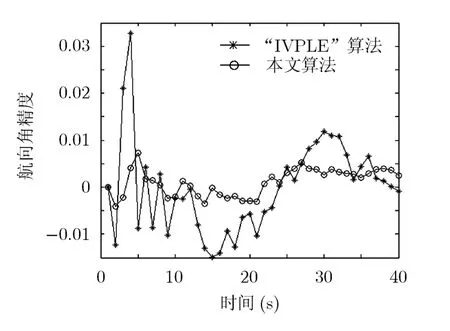
图7 与IVPLE算法目标航向角精度比较

[1] Dogancay Kutluyil and Ibal Gokhan. Instrumental variable estimator for 3D bearing-only emitter localization[C].Proceedings of the 2nd International Conference on Intelligent Sensors, Sensor Networks and Information Processing, Australia, Dec. 2005: 63-67.

[2] Dogancay K. Bias compensation for the bearings-only pseudo linear target track estimator[J]. IEEE Transactioins on Signal Processing, 2006, 54(1): 59-68.

[3] Bishop A N, Anderson B D O, Fidan B, Pathirana P N, and Mao Guo-qiang. Bearing-only localization using geometrically constrained optimization[J]. IEEE Transactioins on Aerospace and Electronic Systems, 2009,45(1): 308-320.

[4] Zhong Zhi-tong and Yang Xiu-ting. The applications of nonlinear Kalman filters in passive tracking with bearing-only measurements [J]. Technical Acoustics, 2008,27(6): 912-916.

[5] 洪少华, 史治国, 陈抗生. 用于纯方位跟踪的简化粒子滤波算法及其硬件实现[J]. 电子与信息学报, 2009, 31(1): 96-100.Hong Shao-hua, Shi Zhi-guo, and Chen Kang-sheng.Simplified algorithm and hardware implementation for particle filter applied to bearings-only tracking [J]. Journal of Electronics & Information Technology, 2009, 31(1): 96-100.

[6] 刘进忙, 姬红兵, 左涛. 纯方位观测的航迹不变量目标跟踪方法[J]. 西安电子科技大学学报, 2008, 35(1): 49-53.Liu Jin-mang, Ji Hong-bing, and Zuo Tao. Trajectory invariable-information target tracking algorithm with bearing-only measurement [J]. Journal of Xidian University(Natural Science), 2008, 35(1): 49-53.

[7] 王鼎, 张莉, 吴瑛. 基于角度信息的结构总体最小二乘无源定位算法[J]. 中国科学, 2009, 39(6): 663-672.Wang Ding, Zhang Li, and Wu Ying. An algorithm of total least squares for passive location based angle information [J].Science in China, 2009, 39(6): 663-672.

[8] 刘忠, 周丰等. 纯方位目标运动分析[M]. 北京: 国防工业出版社, 2009, 4: 29-52.Liu Zhong and Zhou Feng. An Analysis of Targets Motion Based Bearing-only [M]. Beijing: National Defense Industry Press, 2009, 4: 29-52.