非规则曲面共形阵列的优化设计

张玉洁 龚书喜 王文涛 凌 劲

(西安电子科技大学天线与微波技术国家重点实验室 西安 710071)

1 引言

共形天线阵具有低剖面、节约空间以及提供宽角扫描等优点，在现代通信系统中有着广泛的应用。微带天线以其良好的气动外形、易于安装面共形且重量轻、低成本等特性，使之在共形阵列研究中得到了广泛的应用。目前关于共形微带阵列的研究中，大多是基于一些规则曲面，如圆柱面、圆锥面、球面和抛物面等。其中又因柱体是构成各种飞行器的基本结构且具有简单的形式，故大多数的工作是关于圆柱共形微带阵列的研究[1]，此外一些学者对于圆锥面及抛物面共形阵列也做了一定的研究[2−4]。然而，随着共形天线应用领域的飞速发展，共形载体的形状越来越呈现不规则化。为了适应形状更为普遍的共形载体，继而使共形天线得到更广泛的实际应用，对于不规则曲面上共形微带阵的研究具有很大的实际意义。但目前研究工作中对于不规则曲面上共形微带阵的研究却相对较少[5]。Allard[6]提出了一种基于范围分解和互易定理的新方法，用于计算共形在任意形状PEC载体上微带天线的远场方向图。但不足的是在验证该方法正确性的实例中，仍然只采用了共形在圆柱载体上且沿圆柱轴向分布的直线阵，没有进一步证明对于共形在任意载体即非规则载体上的阵列应用该方法的正确性，因而非规则曲面上的共形阵列并没有得到明确的研究。因此，对不规则曲面共形阵方向图的综合需要更进一步的研究。由于共形阵特别是非规则曲面上的共形阵各单元法向均不相同，使得对于共形阵列方向图的分析及设计与平面阵相比更为复杂，对于有些很复杂的非规则曲面的共形阵来说，利用理论分析进行方向图的综合几乎是不可能实现的。在这种情况下，一些优化算法如遗传算法就被考虑用来进行方向图综合，从而改善阵列天线的性能。但目前利用遗传算法进行方向图综合的文献中，大多是较简单的线阵及平面阵，共形阵方面也只是基于简单的规则载体，如圆柱、圆锥等[6]，而对于非规则曲面共形阵相关的研究工作却很少。

针对以上问题，设计了一个新型的H形非规则曲面微带共形阵列。文中采用自适应混合遗传算法(SHGA)对该阵列的辐射方向图进行了优化设计。SHGA将传统的，基于问题知识的启发式搜索算法如模拟退火法(SA)和列表寻优法(TABU)引入到遗传算法中，改善了遗传算法的局部搜索能力差，容易陷入局部最优解的缺点。此外，文中还采用了自适应遗传算子来提高算法的效率和优化质量。因此，相比较于遗传算法，SHGA是一种可以高效准确解决电磁天线问题的优化算法。同时在计算单元天线的3维方向图时，采用仿真软件计算和方向图重构技术相结合，既考虑了单元间的互耦影响以及载体对单元天线方向图的影响，又改善了传统方法在计算天线方向图中对于天线形式的限制问题。

2 阵列结构及微带单元设计

由实际工程经验可知，一般平面阵列的单元间距设计为0.8λ左右，这是考虑到消除栅瓣及单元互耦分析得到的经验值，并且在实际研究工作中得到了应用[7]。在平面阵列单元间距的基础上，考虑到文中采用的阵元数目、阵元尺寸以及非规则载体形状，故设计中取阵列单元中心沿共形曲面的弧线距离为0.75λ。这里，λ为工作波长。天线阵列形式为单排纵向7元阵列，如图1所示。

图1 非规则曲面共形阵结构

Vani[8]提出在微带贴片上开槽能够有效增加微带天线贴片等效电流路径长度，从而实现微带天线的小型化。在文献[8]的研究基础上，结合文中实际情况，首次将H形微带单元作为阵列单元应用到非规则曲面共形阵中，使得天线阵列结构小型化。此外，当H形天线与载体共形时，其谐振频率和带宽受载体形状变化影响剧烈，从而导致阵列性能的下降。考虑到这种影响，在共形天线阵设计中采用了非均匀厚度的共形低剖面H形空气微带单元，单元结构如图2所示，微带天线的长边长度为W，短边长度为L ，微带天线两短边开槽深度为Ls，开槽宽度为Ws，开槽边沿距微带贴片上沿长度为Ps，天线探针馈电，馈电点距离贴片长边距离为F，探针长度与天线中心厚度均为Hc，左右两边厚度为He。

3 共形阵列方向图综合及单元天线3维方向图重构

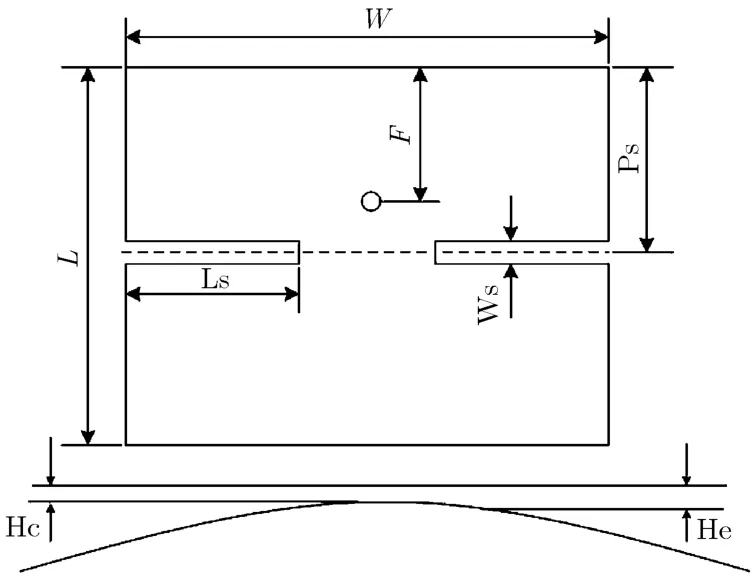
图2 H形微带单元，W=60, L=40, F=11.5, Ps=20,Ws=3.7, Ls=14.2, Hc=2.3, He=4.6, 单位: mm

对于共形阵列来说，阵列单元的位置和指向受到共形载体的影响，因此共形阵列的远场方向图将表示为更一般的形式。基于文献[9]给出的一种阵列方向图表示形式，文中为了更方便的应用，对其进行了变化：

式中N为共形微带阵的单元个数，En为第n个单元的激励幅度，fn为第n个单元的3维辐射方向图，βn为第n个单元的激励相位，u为辐射方向的单位矢量，dn为第n个单元的位置矢量，k为自由空间的波数。

文中采用自适应混合遗传算法(SHGA)对共形阵列方向图进行了综合。GA+SA+TABU的混合方法强化了单纯GA的局部搜索能力，拓展了SA及TABU的局部搜索范围，很大程度上提高了收敛速度和最优解的质量。算法的具体实现过程如下：在解空间随机产生一组初始群体，选择方法采用精英保留策略和无回放余数随机取样混合机制，其中精英保留策略保证了算法最终收敛于全局最优解，无回放余数随机取样法通过个体生存期望值的整数部分安排个体被选中的次数，而对其小数部分按照赌轮选择机制进行选择，直到选满为止。为维护群体的多样性，保证寻优的收敛，交叉概率和变异概率的设计可以随个体适应度和进化阶段的不同而自适应变化。算法中采用的交叉概率Pc及变异概率Pm分别为

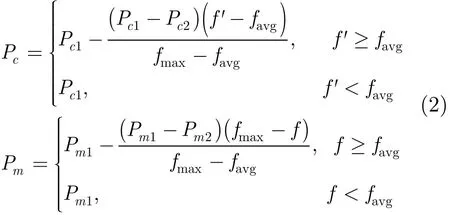
这里fmax和favg分别为当前群体中的最大适应度值和平均适应度值，f'为两个待交叉个体中较大适应度值的个体，f为变异个体的适应度值，Pc1,Pc2,Pm1和Pm2分别设置为0.9,0.6,0.1和0.001。其他各项参数为：初始群体规模为100，最大迭代次数为1350，SA算法中的初始温度为2000，降温系数为0.9。采用Metrolipis接受准则接受恶化解。

遗传算法一般是求最大值问题，而文中所设计的微带共形阵列的方向图优化目标是一个最小值问题，故此优化算法对应的适应度函数表达式应为

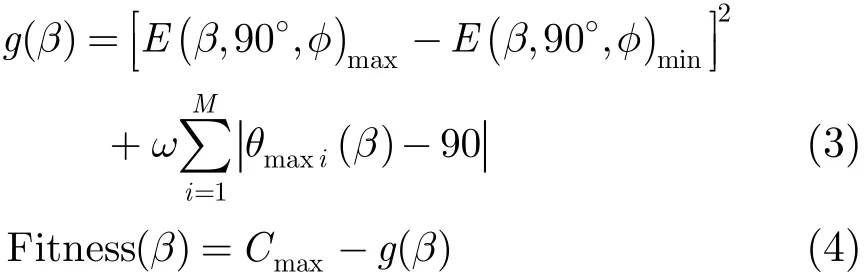
式中Cmax为当前群体中g(β)的最大值，随进化代数变化而变化，E(β,90°,φ)max和E(β,90°,φ)min分别为阵列单元相位为β=(β1, β2,…,βN)时，阵列水平面dB方向图的最大值和最小值；M为φ∈[0°,360°]区间的取样点数，优化中设为4；ω为权系数，其值由共形阵列单元方向图、阵列单元排列形式以及阵列优化目标所决定，优化中设为0.2/M，θmaxi(β)为包含水平面方向图第i个数据点的俯仰面的最大辐射方向，其表达式为

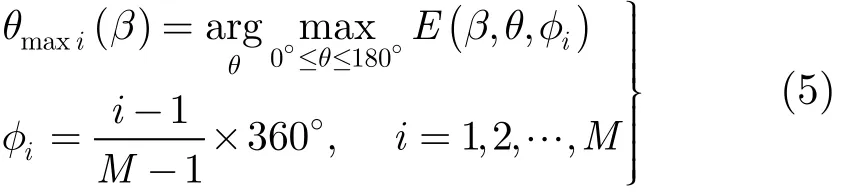
该文的优化目标为共形阵列在水平面为近似全向辐射且俯仰面辐射集中在水平方向。阵列单元采用等幅不同相激励。通过评估式(4)所示的共形阵列适应度函数，SHGA法可以优化得到所对应的阵列单元相位。

如式(1)所示，在进行阵列方向图综合之前，必须得到单元的3维方向图。采用实验的方法获取天线的近似3维辐射方向图不仅工作量大，而且往往也只能得出有限多个面上的辐射方向图。因此，有必要对天线的3维辐射方向图近似计算方法进行研究。在天线3维方向图近似计算方法中，SA算法、4点插值算法，Gvas算法等都有着的广泛应用，但重构结果均不是最优。在此基础上，这里给出了一种改进的3维方向图近似计算方法。令E面和H面分别与水平面和垂直面重合，水平面为θ=90°平面，垂直面为φ=90°平面，天线的水平面和俯仰面归一化场强方向图分别为hor(φ)和vert(θ)。这里利用Ansoft HFSS仿真软件计算得到了相关的hor(φ)和vert(θ)的数据。则

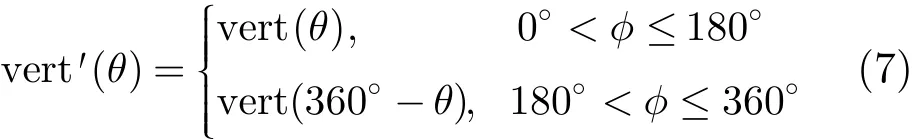
水平面和俯仰面dB方向图可分别表示为

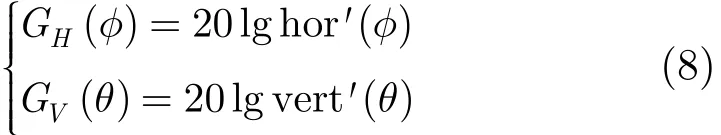
则天线的3维dB方向图可近似为

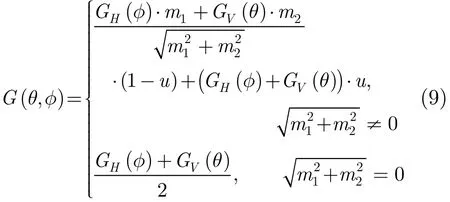
式中u, m1, m2为权系数，其具体表达式为

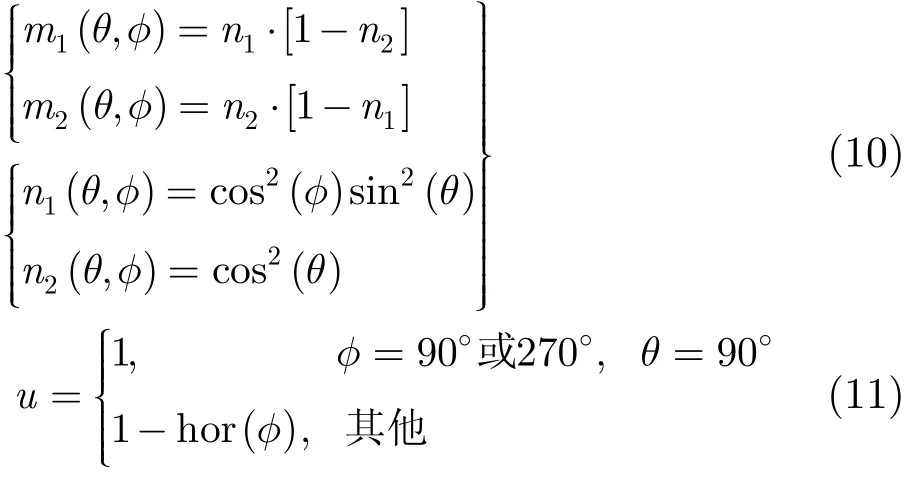
4 优化结果

为了比较不同优化算法的性能，文中同时采用标准遗传算法SGA、遗传算法与模拟退火混合算法GA+SA以及文中所提出的SHGA算法这3种优化算法对文中非规则共形阵的辐射方向图进行了优化设计。图3分别给出了3种优化算法的适应度函数值随进化代数变化的结果图。从图中可以看出，传统的SGA算法优化性能最差，收敛速度慢且极易陷入局部最优解。GA+SA混合算法收敛速度虽远快于SGA算法，但陷入局部最优解后同样无法跳出。而文中所提出的SHGA算法，收敛速度在3种算法中最快，且在陷入局部最优解后能够利用算法自身强大的局部搜索能力跳出局部最优而最终达到全局最优解。

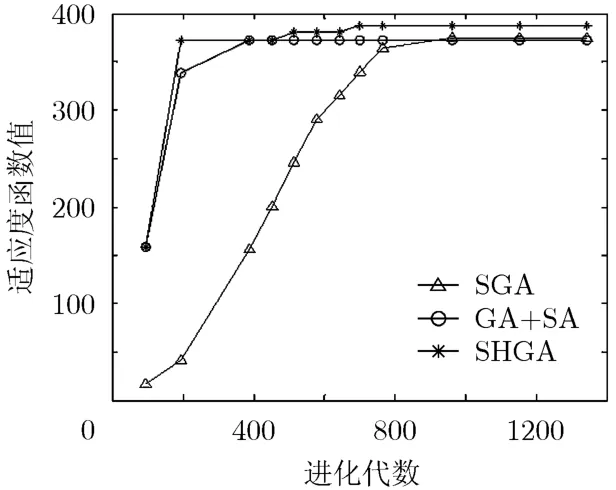
图3 3种优化算法的性能对比图

为了对比优化后的辐射方向图性能，这里给出了优化前的非规则共形阵的辐射方向图，单元天线为等幅同相激励。分析结果如图4所示。由图可知，优化前的共形阵水平面辐射方向图在φ=180°时场强幅值较大，并在φ=160°和φ=200°时场强幅值较小，全向性较差；俯仰面方向图也没有集中辐射在水平方向，而是存在多个主瓣，造成了水平方向辐射的能量损失。

采用SHGA算法优化得到的单元相位结果如表1所示。根据优化结果，重新分析计算了非规则曲面微带共形阵列。为了确定优化结果是否正确，我们采用了两种仿真软件进行计算以作对比。文中采用的仿真软件分别是Ansoft HFSS和IE3D，均得到了较好的计算结果。图5分别给出了中心频率在2500 MHz两种计算软件的水平面和俯仰面的归一化场强方向图。从结果图可以看出，优化后的方向图在水平方向几乎达到了全向辐射，并且俯仰面方向图集中辐射在水平方向，这也是该文优化的目标之一。

表1 单元相位的优化结果

在工程实践中，由于加工精度、网络损耗等影响，单元的实际激励相位会与仿真数据产生误差。根据工程经验，相位分布通过调试可以控制在一定范围内，比如：相位误差最大在±15°的范围内。在相位误差的约束下，对所有单元(每一个单元独立)每次随机产生一组均匀分布在相位误差范围内的相位误差数据叠加到原来设计的相位分布上进行仿真分析。对于随机产生的一组相位误差，图6给出了考虑到该组相位误差后辐射方向图的仿真结果。由图5和图6的结果对比可以看出，在考虑相位误差后，相位误差对于俯仰面辐射方向图的影响较大，在部分角度上的方向图改变较大，但总体形状大体一致。对于水平面辐射方向图，相位误差对其影响较小，前后基本一致。这说明该文利用自适应混合遗传算法对共形天线阵的方向图进行优化得到的相位分布合理。

5 结论

图4 在2500 MHz频率下的优化前共形阵列辐射方向图

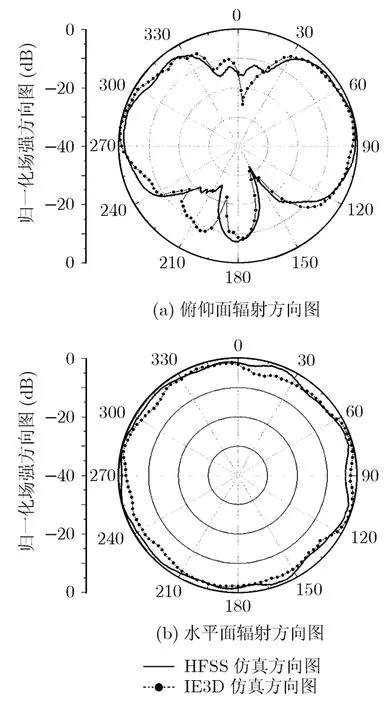
图5 未考虑相位误差时在2500 MHz 频率下的共形阵列辐射方向图

图6 考虑相位误差时在2500 MHz 频率下的共形阵列辐射方向图

文中利用SHGA法对一种H形非规则曲面的微带共形阵列辐射方向图进行了优化设计。优化后的方向图在水平方向几乎达到了全向辐射，俯仰面方向图集中辐射在水平方向。同时，文中分析了在一定相位误差存在情况下对于共形微带阵列辐射方向图的影响情况，得出文中利用自适应混合遗传算法对共形天线阵的方向图进行优化得到的相位分布合理，研究成果可用于后续的工程实践中。此外，文中采用的非规则曲面载体形似于某些飞行器的腔体，这对于将来研究飞行器腔体的共形阵列提供了很大的参考价值。从优化结果可以看出，文中所提出的优化算法对于非规则曲面共形微带阵列的研究具有一定的参考价值。

[1] Werner D H, Allard R J, Martin R A, and Mittra R. A reciprocity approach for calculating radiation patterns of arbitrarily shaped microstrip antennas mounted on circularly cylindrical platforms. IEEE Transactions on Antennas Propagat., 2003, 51(4): 730-738.

[2] Gao De-yuan, Qi Zi-sen, Wang Bu-hong, and Guo Ying.Performance analysis of high resolution DOA estimation for conical conformal array. WiCOM 4th International Conference. Dalian, Oct 12-14, 2008: 1-4.

[3] Morton T E and Pasala K M. Pattern synthesis and performance of conical arrays. Proceedings of the Thirty-Sixth Southeastern Symposium. Atlanta, GA, United States, 2004: 145-149.

[4] Wang Bu-hong, Meng Ling-qin, and Guo Ying. Pattern synthesis of double-curved conformal paraboloidal array.Antennas and Propagation Society International Symposium.San Diego, CA, United states, July 5-12, 2008.

[5] Josefsson L and Persson P. Conformal Array Antenna Theory and Design. New Jersey:Institute of Electrical and Electronics Engineers, Inc., 2006, Chapter 1, 4-9.

[6] Allard R J, Werner D H, and Werner P L. Radiation pattern synthesis for arrays of conformal antennas mounted on arbitrarily shaped three-dimensional platforms using genetic algorithms. IEEE Transactions on Antennas Propagat., 2003,51(5): 1054-1062.

[7] 杜卫民. 低副瓣平面阵列天线设计. [硕士论文], 西安电子科技大学, 2008.Du Wei-min, Low-sidelobe planar array antenna design. [ MA.dissertation], Xidian University, 2008.

[8] Vani R M, Farida S F, and Hunagund P V. A study on rectangular microstrip antenna with group of slots for compact operation. Microwave and Optical Technology Letters, 2001, 40(5): 396-398.

[9] Lu Z B, Zhang A, and Hou X Y. Pattern synthesis of cylindrical conformal array by the modefied particle swarm optimization algorithm. Progress In Electromagnetics Research, 2008, PIER 79, 415–426.