二进制传感器网络加权目标跟踪算法研究

孙晓艳 李建东 陈彦辉 张文柱 姚俊良

①(西安电子科技大学综合业务网理论和关键技术国家重点实验室 西安 710071)②(西安外事学院信息工程学院通信电子工程系 西安 710077)

1 引言

无线传感器网络是近年来的研究热点，其广泛应用于军事、环境观测、预报系统、医疗护理、智能家居等方面[1,2]。而目标跟踪被认为是无线传感器网络的基本职能之一。二进制传感器网络由于其低廉的布设代价、体积小、低能耗、以及传感器节点简单的操作和数据通信，正得到越来越多的关注。

在二进制传感器网络中，若传感器节点感测到目标的存在，即目标在传感器节点的感测范围内，则传感器节点产生“1”bit；反之，产生“0”bit。融合中心根据传感器节点产生的二进制比特计算目标单点的位置估计、产生目标轨迹实现对目标的跟踪。文献[3]首次提出了二进制传感器网络中的协同跟踪算法。在协同跟踪算法中，目标以匀速穿过网络，传感器节点记录目标在其感测区域内停留的时间并与其他节点进行交互。文献[3]采用了3种加权机制，等权值(各个感测节点的权值相同)、感测持续时间加权和启发式加权。经仿真验证，感测持续时间加权性能最好。但是，采用感测时间加权的协同跟踪算法要求网络中的节点严格同步。文献[4]提出了感测次数加权的二进制传感器网络目标跟踪算法，即传感器节点记录其感测到目标的次数，并以此作为目标单点位置计算的权值。采用感测次数作为权值的算法虽然解决了算法对节点同步的依赖性，但其跟踪精度不高。近年来，粒子滤波算法在目标跟踪中得到了广泛的应用。文献[5-7]将粒子滤波算法用于二进制传感器网络目标跟踪并获得了较高的跟踪精度，但计算量大。

本文提出了距离加权和基于预测的距离加权二进制传感器网络跟踪算法。距离加权算法解决了已有算法中权值不能实时反映目标与感测节点距离关系的问题，实现了以较高的精度跟踪目标。基于预测的距离加权算法通过在融合中心预测并计算距离信息，从而在保证跟踪精度的前提下避免了距离信息的传输。

2 系统模型和问题描述

本文考虑的传感器网络采用格型分布，网络中的节点周期性地感测目标，并将感测结果发送给融合中心，且融合中心已知节点的位置。若节点感测到目标位于其感测范围内，则发送“1”bit到融合中心；否则不发送任何数据以节省能量。由于本文所考虑的传感器节点类型为二进制传感器节点，所以节点根据感测到的目标信号功率大小来判断目标是否出现在其感测范围内。本文考虑实际传输条件，感测节点收到的目标信号强度为

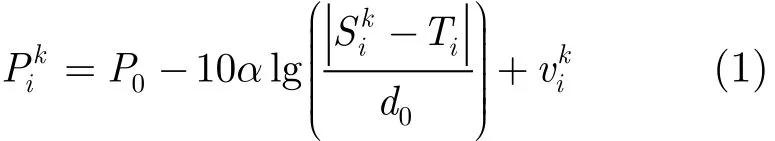
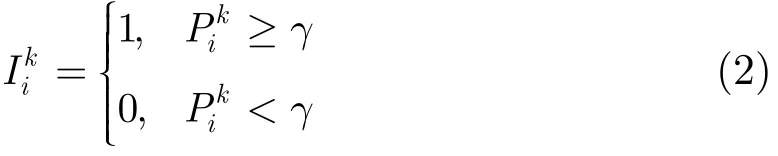
在目标定位、导航和跟踪应用的研究中，广泛采用目标状态线性变化而测量值非线性变化的运动模型，其中目标运动模型为

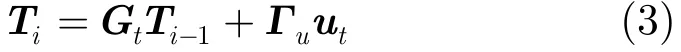
其中

Ti表示目标在2维笛卡尔坐标系中的位置和速度；Gt和Γu是已知的目标状态转移矩阵；ts为采样时间间隔，ut是2×1的表示零均值方差为Cu的高斯噪声；Cu表示目标的加速度，为不失一般性假设

因此，二进制传感器网络目标跟踪问题的实质就是如何根据二进制传感器节点的感测信息估计目标位置

3 距离加权目标跟踪算法

在二进制传感器网络中普通节点仅将其感测结果的1 bit信息发送给融合中心，因此融合中心仅能根据当前时刻的普通节点的感测结果以及各个普通节点的位置来计算目标的单点位置估计。本文考虑距离加权算法来计算目标的单点位置估计。

在文献[3]和文献[4]的算法中无论目标做直线运动还是曲线运动，普通节点的感测持续时间越长，感测次数越大，不能说明目标距离该普通节点的距离就是最近的，例如图1所示。在图1中，目标分别以曲线从A点运动到B点和以曲线从C点运动到D点，均先后经过节点S1和S2。在t3采样时刻，节点S1的感测持续时间和感测次数大于节点S2的感测持续时间和感测次数，但是目标节点距离S2更近，所以文献[3]和文献[4]中的感测持续时间和感测次数加权不能说明目标和感测节点间的实时距离关系。因此本文考虑距离加权，即用每个采样时刻目标和感测的普通节点的距离直接作为进行目标单点的位置估计的权值，这样距离权值可以实时地反映目标与各个感测的普通节点之间的关系。

设采样时刻i共有N个节点感测到目标，则各个感测节点将接收到的信号功率与预设门限γ比较产生感测信息。若节点的感测信息=0，则节点不再进行任何计算也不向融合中心发送数据；若节点的感测信息=1，则节点首先根据式(1)计算其与目标之间的距离为

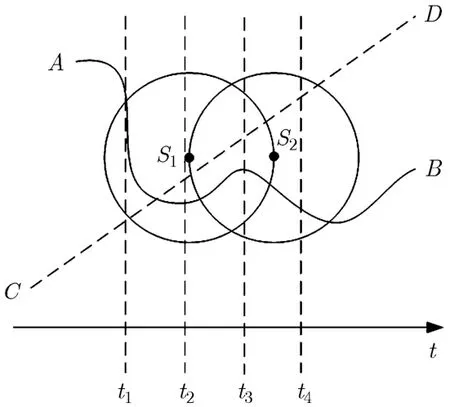
图1 目标运动轨迹与感测节点的实时关系

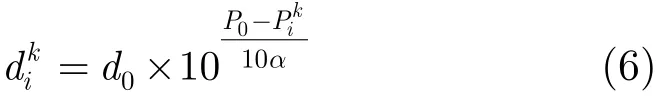
从而，融合中心采用各个节点的感测信息、已知的节点位置和计算的距离权值计算目标位置估计。

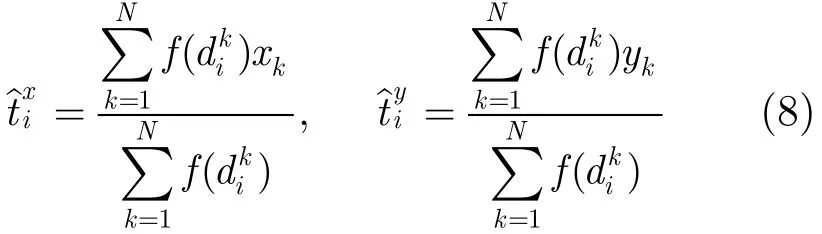
距离加权(DW)目标跟踪算法具体描述如下。

DW算法描述：采样时刻i；

节点：

(1)根据接收信号强度产生感测信息

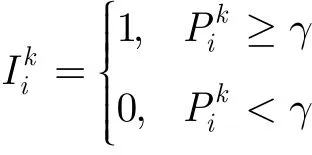
(3)节点将产生的感测信息和计算的距离信息发送给融合中心。

融合中心：

(2)根据距离权值计算目标位置估计

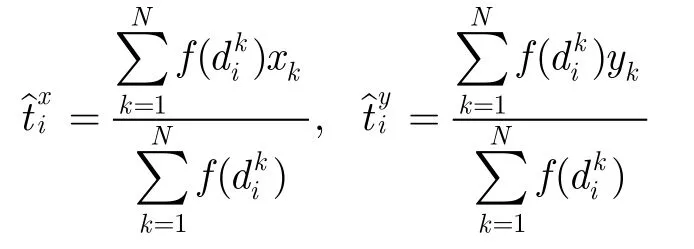
4 基于预测的距离加权算法

传感器网络中的节点采用电池供电，所以其能量受限。传感器节点的通信/能耗比为1000，Rockwell WINS (Wireless integrated network sensors)传感器的通信/能耗比为1500～2700[8]。传感器节点的通信耗能主要包括发送和接收时的能量消耗，其具体能耗与发送和接收的数据大小有关。发送和接收的数据越大，通信能耗也越大。因此，为了减少距离加权目标跟踪算法中的通信耗能，本文又提出基于预测的距离加权目标跟踪算法。

在基于预测的距离加权算法中，感测节点首先根据接收信号强度判决产生感测信息，然后只将感测信息发送给融合中心。融合中心已经产生的目标位置估计采用递归最小二乘预测[9](RLS)下一时刻目标与各个节点间的距离，然后在下一时刻采用预测的距离根据距离加权算法计算目标的位置估计。

设RLS滤波器长度为M，在前M个时刻(i≤M)RLS滤波器由于没有足够的信息进行预测，也不能采用距离加权，所以本文在前M个时刻采用等权值进行目标位置估计，如式(9)所示。

在第M+1个时刻以后，融合中心首先将前M个时刻的目标目标位置估计作为RLS滤波器的输入参数估计下一时刻目标的位置；然后根据预测的目标位置计算下一时刻目标与节点间的距离并在下一时刻采用距离加权计算目标位置估计，如公式(10)所示。

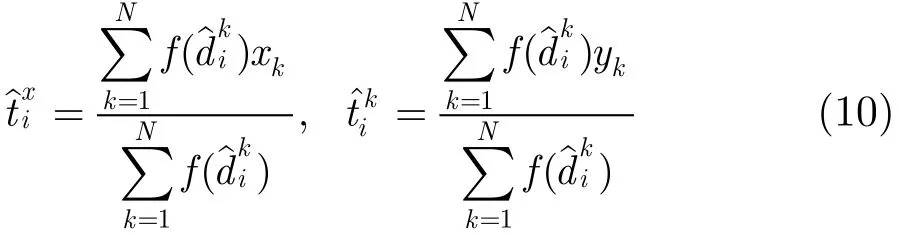
基于预测的距离加权算法具体描述如下：

采样时刻i，RLS滤波器长度为M；

节点：根据接收信号强度产生感测信息

融合中心：

if i ＜M采用等权值计算目标位置估计

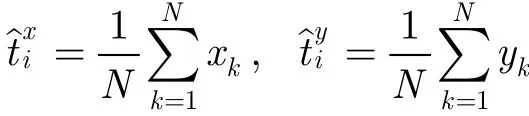
else if i= =M采用等权值计算目标位置估计

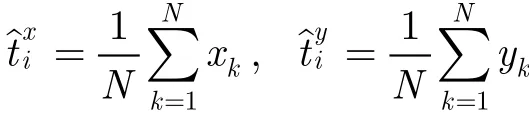
根据已有的前M个目标位置估计采用RLS预测目标位置；

else if i＞M根据上一时刻产生的预测距离采用距离加权计算目标位置估计

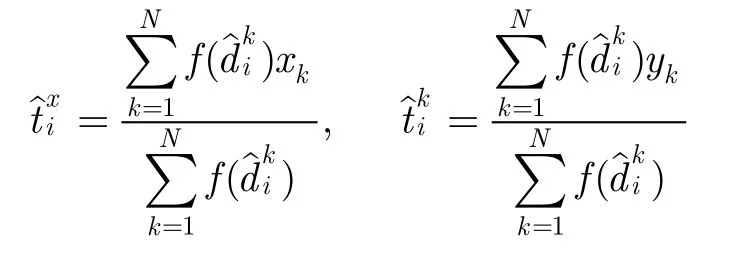
根据已有的前M个目标位置估计采用RLS预测目标位置；

5 仿真实验和结果分析

本节通过两组实验验证本文所提算法的有效性，同时和3种已有算法进行比较，这3种算法分别为：文献[3]中的感测时间加权(TW)、文献[4]中的感测次数加权(NW)以及文献[5]中的粒子滤波(PF)算法。仿真中的具体仿真参数如表1所示。

表1 仿真参数设置

实验1 一方面，感测时间加权算法仅适用于目标匀速运动，而感测次数加权算法消除了感测时间加权算法对节点同步的要求，所以在目标匀速运动模型中，本文对感测时间、感测次数和距离加权算法的性能进行比较。另一方面，粒子滤波算法的精确估计性能主要依赖于目标状态的随机性，因此在目标变速运动模型中，对距离加权算法和粒子滤波算法的性能进行比较。

图2给出了距离加权算法与已有算法的性能比较。图2(a)中目标采用匀速运动模型，其中所比较的3种算法在各个归一化误差区间内的概率如表2所示。所比较的3种算法在归一化概率区间[0.4,0.5)和[0.5,0.6)内的概率很小，可以认为是小概率事件，因此忽略不计。而感测时间加权算法的归一化误差主区间为[0.1,0.2)，感测次数加权算法的归一化误差主区间为[0.1,0.3)，距离加权算法的归一化误差主区间为[0,0.2)。图2(b)中采用变速运动模型，对距离加权算法和粒子滤波算法进行了比较，距离加权算法性能明显优于粒子滤波算法性能。因此，距离加权目标跟踪算法优于已有算法性能，能够更加精确地跟踪运动目标。

实验2 本实验中，首先仿真讨论RLS滤波器长度对基于预测的距离加权算法性能的影响；然后对距离加权算法和基于预测的距离加权算法性能进行比较；最后分析了距离加权算法和基于预测的距离加权算法的通信能耗。

图3考虑了不同RLS滤波器长度对基于预测距离加权算法性能的影响。由文献[9]知，RLS的学习曲线需要经过2M次迭代才能收敛，因此在应用中应该选择尽可能小的M。此外，由仿真结果知，M对预测距离加权算法性能影响不大，所以在应用中本文选择M=1。图4给出了距离加权算法和预测距离加权算法的性能比较，由于预测距离加权算法目标位置估计归一化误差落入区间[0.3,0.4)、[0.4,0.5)及以后区间的概率非常小，认为是小概率时间忽略不计。所以预测距离加权与距离加权算法的归一化误差主区间重合，证明预测距离加权算法的有效性。

假设感测节点向融合中心发送1 bit信息需要消耗1个单位的能量，则在相同的条件下距离加权和基于预测的距离加权算法的发送能耗的差别在于发送数据的比特数。基于预测的距离加权算法中感测节点只发送1 bit的感测信息；距离加权算法中感测节点需要发送1 bit的感测信息和计算的距离信息。仿真中节点感测半径为125 m，则可以用7个bit表示计算的距离信息。图5给出各个感测时刻，距离加权算法和基于预测的距离加权算法的网络总能耗，其中当目标离开监测区域时基于预测距离加权算法的网络单位总能耗仅为距离加权算法网络单位总能耗的14.29%。

表2 目标匀速运动时算法归一化误差区间概率分布

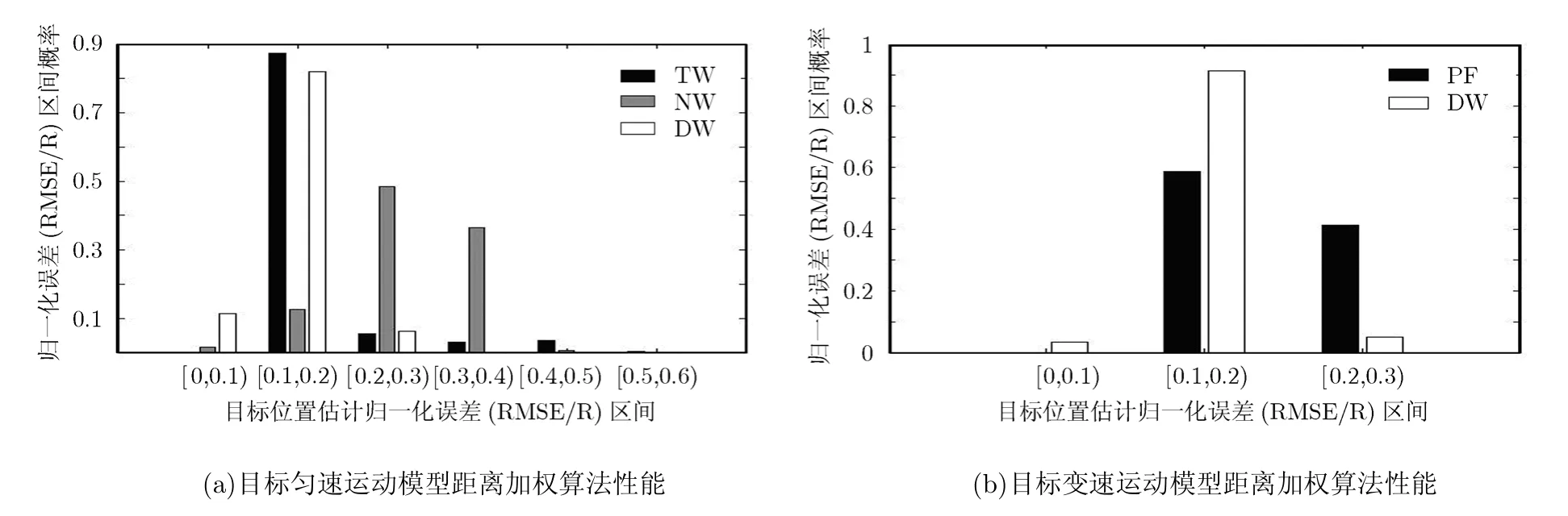
图2 距离加权目标跟踪算法性能

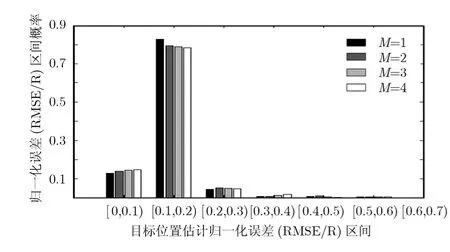
图3 不同RLS滤波器长度基于预测距离加权算法性能

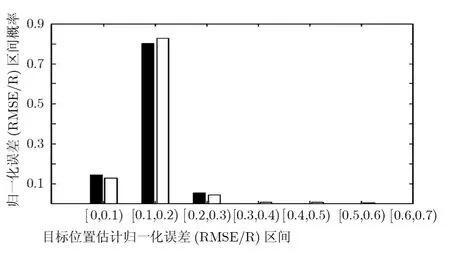
图4 距离加权算法与基于预测距离加权算法性能比较

图5 距离加权和基于预测距离加权算法的网络单位总能耗

因此，基于预测的距离加权算法不仅保证了跟踪精度而且通过避免距离信息的传输大大减少了传感器网络中的通信能耗。

6 结束语

本文提出了距离加权和基于预测的距离加权目标跟踪算法。距离加权算法通过采用实时反映目标与感测节点间距离关系的距离权值保证了跟踪精度。基于预测距离加权算法在距离加权算法的基础上通过减少距离信息的传输进一步减少距离加权算法中的通信能耗。后续的研究重点是研究传感器网络节点部署和网络覆盖对基于预测距离加权算法的性能影响。

[1] Akyildiz I, Sun W, and Sankarasubramaniam Y, et al.. A survey on sensor networks. IEEE Communications Magazine,2002, 40(8): 102-114.

[2] 陈积明，张艳平，曹向辉等. 基于声强的无线传感器网络目标跟踪方法研究[J]. 电子与信息学报，2009, 31(11): 2791-2794.Chen Ji-ming, Zhang Yan-ping, and Cao Xiang-hui, et al..Acoustic energy based scheme for target tracking in wireless sensor networks[J]. Journal of Electronics & Information Technology, 2009, 31(11): 2791-2794.

[3] Mechitov Kirill, Sundresh Sameer, and Kwon Youngmin, et al.. Cooperative tracking with binary-detection sensor networks[R]. Technical Report UIUCDCS-R-2003-279,Department of Computer Science, University of Illinois at Urbana-Champaign, 2003.

[4] 李煜，程远国，杨露菁. 二元探测传感器网络的递推加权质心目标定位算法[J]. 海军工程大学学报，2008, 20(5): 42-45.Li Yu, Cheng Yuan-guo, and Yang Lu-jing. A resursive weighted centroid algorithm for object location in binary sensor networks[J]. Journal of Naval University of Engineering, 2008, 20(5): 42-45.

[5] Djuric P M, Vemula M, and Bugallo M F. Signal processing by particle filtering for binary sensor networks. Proc. IEEE 11th Digital Signal Processing Workshop & IEEE Signal Processing Education Workshop, Millenia Singapore, 2004:263-267.

[6] Vemula M, Bugallo M F, and Djuric P M. Particle filtering-based target tracking in binary sensor networks using adaptive thresholds. Proc. The 2nd IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing, Virgin Islands, American, 2007: 17-20.

[7] Djuric P M, Vemula M, and Bugallo M F. Target tracking by particle filtering in binary sesnsor networks. IEEE Transactions on Signal Processing, 2008, 56(6): 2229-2238.

[8] Raghunathan V, Schurgers C, and Partk S, et al..Energy-aware wireless microsensor networks. IEEE Signal Processing Magazine, 2002, 19(2): 40-50.

[9] 赫金(Haykin.S.)著，郑宝玉等译. 自适应滤波器原理(第4版)[M]. 北京：电子工业出版社，2006-11-1, 344-366.