无线传感器网络分布式一致时间同步协议的收敛分析及加速设计
2010-03-27刘勇攀杨华中
李 立 刘勇攀 杨华中 汪 蕙
(清华大学电子工程系清华信息国家实验室 北京 100084)
1 引言
时间同步协议是传感器网络的研究热点之一。早期的全网时间同步协议多是集中式的,如传感器网络时间同步协议[1](Timing-sync Protocol for Sensor Networks,TPSN)等。它们由根节点发起同步,通过建立全网路由来传播同步消息。接收到同步消息的节点根据消息中携带的时间信息调整本地时间,最终使全网节点都与根节点的时间同步。集中式时间同步协议存在以下几个缺点。(1)可扩展性差。新加入的节点需要等待路由建立后才能开始同步。(2)抗毁性差。一旦同步路由出现中继节点失效的情况,部分节点将由于接收不到同步消息而失去同步。(3)同步误差会沿同步路由累积[2]。距离根节点的跳数越多,误差越大。(4)同步路由的建立和周期性维护会消耗大量的能量和带宽资源。
近年来出现了分布式的时间同步协议[3−8],它们不需要建立全网路由来分发同步消息,从而避免了集中式协议的上述缺点。在文献[3]提出的同步协议中,节点估计自己与根节点的时间相位差,并利用分布式融合使全网节点与根节点保持时间同步。由于文献[3]中的同步协议依赖于根节点提供网络参考时间,它在抗毁性方面存在问题。一旦根节点失效,需要重新选出根节点并与之建立同步。基于分布式一致的全网时间同步(Distributed Consensus Time Synchronization, DCTS)协议[4−8]通过邻居节点间的信息融合,使全网节点的时间都同步到一个虚拟的时间,避免了根节点失效所带来的全网重新同步的问题。由于DCTS依赖于扩散来传递同步信息,导致其收敛速度慢于集中式同步协议,这是制约其在网络中广泛使用的一个瓶颈。现有提高DCTS收敛速度的方法主要是构造二阶迭代矩阵[6],这种方法的缺点在于需要计算全网邻接矩阵的特征值来确定迭代矩阵的参数,而大规模网络的邻接关系通常难以获得。此外,传感器节点的处理器也没有计算大规模矩阵特征值的能力。
本文通过将DCTS的迭代过程映射到马尔可夫链的状态转移过程来分析其收敛特性,推导出DCTS在循环网中的收敛速度决定于网络规模与节点邻居数的比值,并通过仿真实验证实该结论对于节点近似均匀分布的规则网络(类均匀规则网)和节点近似均匀分布的非规则网络(类均匀网)也成立。此外,DCTS在类均匀网的收敛速度还受到节点邻居数分布的影响。基于此,本文提出通过调整网络邻居数分布来加速DCTS的分布式算法。仿真结果表明该算法能有效提高DCTS在类均匀网中的收敛速度。
本文结构安排如下:第2节介绍DCTS的数学模型;第3节基于马尔可夫链分析DCTS的收敛特性;第4节提出基于邻居数分布调整的DCTS加速算法;第5节通过仿真对加速算法的效果加以验证;最后给出了全文的总结。
2 DCTS的数学模型
节点vi的本地时间ci(t)可用一阶线性方程ci(t)=fi⋅t+pi表示,其中fi和pi分别是vi的晶振频率以及初始相位,t是真实世界时间。由于不同节点的频率存在细微差别(典型值为1~100 ppm),所以即使所有节点同时开机,它们的本地时间也会随着时间推移出现偏差,这就是需要时间同步协议的原因。
DCTS包括本地估计、交换和更新同步信息3个步骤。这里的同步信息,可以是节点的本地时间[4],也可以是节点估计的虚拟参考时间的频率和相位[5],但无论交换何种同步信息,其一致性操作都是一样的。由于本文的重点在于分析和加速一致性同步的收敛,所以不区分这些同步信息,统一把它们视为节点的时间信息ti。
DCTS的执行过程可以描述为:每个节点通过与邻居节点交换时间信息,把自己下一时刻的时间信息更新为自己及邻居节点当前时间信息的加权和。于是,节点vi本地时间信息的迭代更新过程可以用数学模型式(1)来表示,其中m为迭代次数,Ni为vi的邻居节点集合,wij表示vi更新时间信息时节点vj对应的权重。
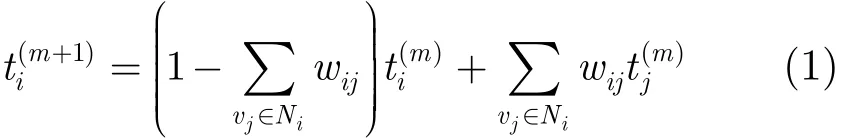
一个网络可以用图的方式表示为N(V,E),其中V={v1,v2,…,vn}表示节点集合,E对应于节点间的单跳通信链路集合E={(i,j)}。假设网络是强连通的,节点间的通信双向可达。令t(m)=(,,…,)为网络节点在m时刻的时间信息向量,W为一阶更新迭代矩阵,DCTS的迭代过程可用矩阵形式(2)来表示
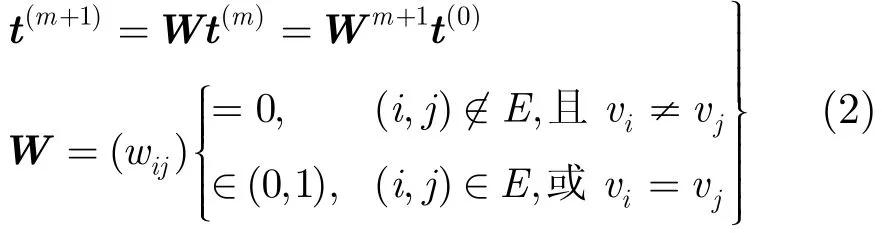
3 基于马尔可夫链的DCTS的收敛特性分析
文献[3]曾将算法的迭代过程映射到马尔可夫域,导出了算法收敛速度与网络边连通度、根节点邻居数和网络规模等参数的关系。由于网络边连通度需要知道全网邻接关系才能获得,且难以通过节点的本地调整加以改变,所以文献[3]中的结论无法用于设计分布式的DCTS加速算法。本文采用马尔可夫链的相关理论来分析DCTS算法的收敛特性与其他网络参数间的关系。
3.1 DCTS的收敛性
首先把DCTS的迭代过程映射为马尔可夫链的状态转移过程。映射关系如式(3),其中网络中的节点对应于马尔可夫链的各个状态S={s1,s2,…,sn},为区别于迭代矩阵W,用P表示马尔可夫链的转移概率矩阵。
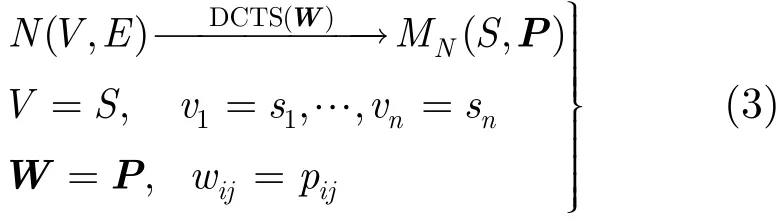
在强连通且节点数有限的网络中,DCTS迭代映射得到的马尔可夫链MN是有限不可约遍历链。根据马尔可夫链的相关理论可知,存在正整数k,使Pk>0,且limm→→Pm=1πT,其中π是马尔可夫链MN的唯一稳态分布,是满足1Tπ=1的正列向量。由式(4)可知,随着迭代次数增加,各节点的时间信息将趋于一致,即达到同步。
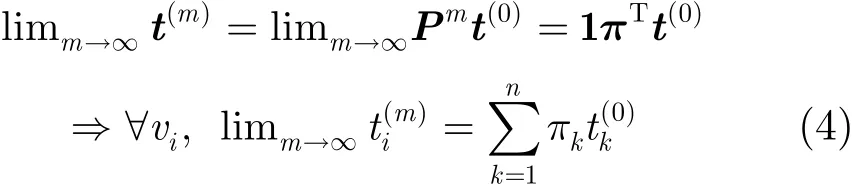
文献[4]在设计迭代矩阵W时,要求wij=wji。此时W是双随机的,马尔可夫链有均匀稳态分布π=(1/n,1/n,…,1/n)T,各节点最终收敛到初始时间信息的平均值11Tt(0)/n。文献[7]中的迭代矩阵定义如式(5)所示,其中di表示节点vi的度,即邻居节点数。下面的分析都基于迭代矩阵式(5)进行。
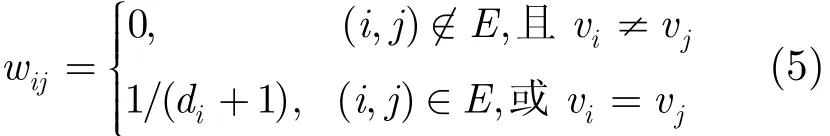
在非规则网络中,节点的邻居数各不相同,迭代矩阵式(5)不满足双随机条件,节点收敛到它们初始时间信息的加权平均值为
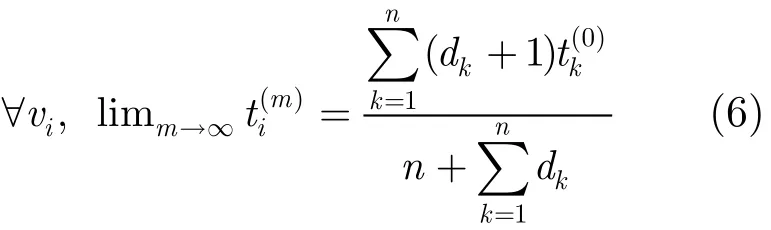
3.2 DCTS收敛速度的分析
DCTS中节点的时间信息达到同步等效于其映射的马尔可夫链MN收敛到稳态。由于MN遍历,且时间可逆(对于MN的任意两个状态sisj,有πipij=πipji),MN的转移概率矩阵P的特征值满足1=λ1>λ2,…,λn>−1。MN的收敛速度取决于矩阵P的模第二大特征值λ*=max(λ2,|λn|),其收敛所使用的迭代次数为m=1/logk(1/λ*)[9]。
时间可逆的马尔可夫链,其转移概率矩阵的模第二大特征值满足Cheeger’s不等式[10],即1-2Φ≤λ≤1−Φ2/2,其中Φ称为马尔可夫链的导通系数,可用式(7)计算。S*是马尔可夫链所有状态的一个子集,其稳态分布之和满足πi∈(0,1/2]。
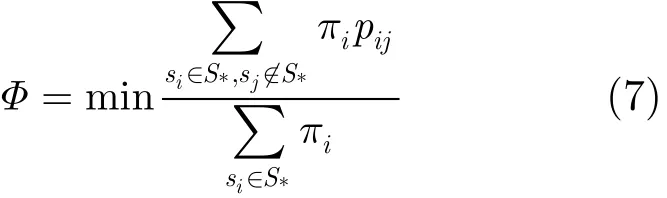
循环网中DCTS收敛速度的界 首先分析DCTS在图1所示的循环网C中的收敛速度。循环网是规则的,每个节点有相同邻居数,设为d。根据式(5)可知在循环网中,DCTS的迭代矩阵W的所有非零元素都等于1/(d+1),且映射得到的马尔可夫链MC有均匀稳态分布。于是,式(7)可简化为式(8),其中|C(S*,)|表示连接节点子集合S*和其补集S*的割边数,|S*|表示集合S*所包含的节点个数。
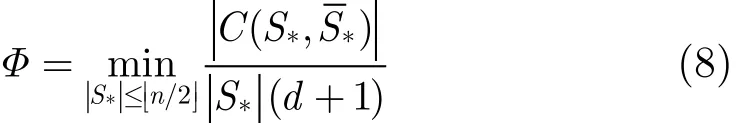
循环网的最小割边数与所选择的节点子集S*的
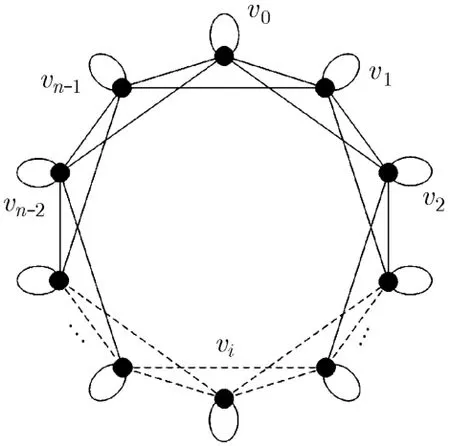
图1 循环网C
大小有关,可具体表示为式(9),其中S+表示给定集合大小为|S+|时所选择的有最小割边数的节点子集。

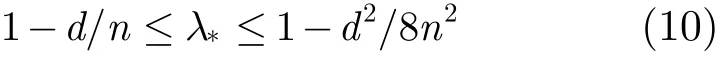
当网络规模较大时,d/n和d2/8n2趋近于0,λ*趋近于1,收敛速度m≈1/(1-λ*)[9]。DCTS在循环网中的收敛速度可近似表示为式(11),说明DCTS在循环网中的收敛速度与网络规模与节点邻居数的比例n/d相关。

3.3 类均匀网中DCTS的收敛速度分析
3.2 节得到了循环网中DCTS收敛速度与网络规模和邻居数的关系。由于实际的传感器网络不会是循环网,所以需要分析DCTS在更一般的网络结构中的收敛速度。
3.3.1 类均匀网的定义 传感器网络可以采用在监测区域里均匀布置节点的方式构成。假设监测区域为矩形。把整个监测区域划分为若干个等面积的小矩形,在每个小矩形的顶点布置一个传感器节点,得到如图2中虚线所示的格子形网络。由于布置时的偏差或是受到外力的影响,实际网络的节点不会如格子形网络中那样整齐排列。给图2中每个节点的位置随机加上一个正的偏移向量(向量的模小于格子形网络中相邻节点距离的一半),得到如图2中实线所示的“类均匀网”。这里的“类均匀”是指监测区域单位面积内的节点个数基本相等。
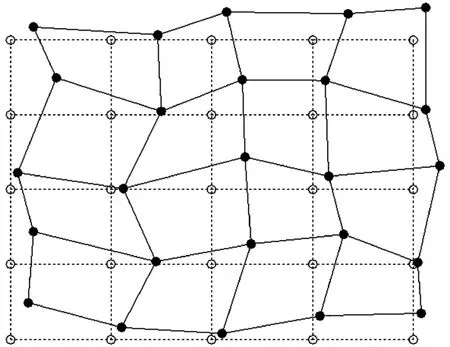
图2 均匀网络和类均匀网络
当节点的传输半径一定时,位于网络边缘的节点的邻居数少于位于网络中心的节点,类均匀网是非规则的。假设通过调整传输半径,使网络中的每个节点都有相同的邻居数,可以得到类均匀“规则”网。如果类均匀“规则”网中所有的节点都有d个邻居,它称为d-规则的。类均匀网和类均匀规则网比循环网具有更一般的传感器网络形态。
3.3.2 类均匀网中DCTS的收敛速度 首先测试DCTS在类均匀d-规则网中的收敛速度。比较下面两种情形:(1)邻居数d不变,网络规模n增加;(2)网络规模和邻居数同比例增加,即保持n/d不变。图3(a)标出了DCTS使节点时间的相对误差小于10−6所需要的迭代次数的比较。仿真结果表明式(11)中的结论在类均匀规则网中也成立。随着网络规模的增加,仅保持邻居数d不变会导致DCTS的收敛迭代次数近似线性地增加;而保持n/d不变可以使收敛速度维持在一个相对稳定的值。
随后本文在4个规模为100的类均匀网中测试了DCTS的收敛速度。测试结果如图3(b)和图3 (c)所示,其中也同时标出了每个网络中邻居数分布的均值和标准差。可以看到,由于类均匀网中节点的邻居数不同,邻居数分布的均值和方差会共同影响DCTS的收敛速度。当邻居数分布标准差较小、网络近似于规则时,节点邻居数的均值决定DCTS的收敛速度(图3 (b))。反之,当节点邻居数相差较大时,邻居数分布的方差也会影响DCTS的收敛速度(图3 (c))。
4 DCTS加速算法
第3节的分析和实验结果表明,节点的邻居数分布会影响DCTS在类均匀网中的收敛速度。由于传感器节点可以动态地调整其无线收发机的发射半径来增加或减少邻居节点,所以可以通过改变节点的邻居数分布来加速DCTS收敛。
4.1 算法描述
加速算法包括初始化和分布式邻居数调整两部分。初始化部分负责为每个节点构造本地邻居表。其执行过程描述如下:(1)节点vi设置发射半径为最低等级,发送“请求邻居消息”,其中包括发送节点ID和当前发射半径等级;(2)节点vj如果是首次接收到来自vi的“请求邻居消息”,则按照“请求邻居消息”中的发射半径等级调整发射功率,回复“请求邻居应答消息”,报告自己的ID;(3)当节点vi接收到vj回复给自己的“请求邻居应答消息”,在邻居表中记录下该节点的ID,及与其通信所需要的发射半径;(4)节点vi提高发射半径,重复步骤(1)-步骤(4)直至发射半径等级到达最大。初始化完成后,本地邻居表中的邻居节点按照其与vi通信所需的发射半径等级升序排列。由于随着节点发射半径的调整,邻居数也会相应改变,用“当前邻居数”表示节点vi在当前发射半径下的邻居数。
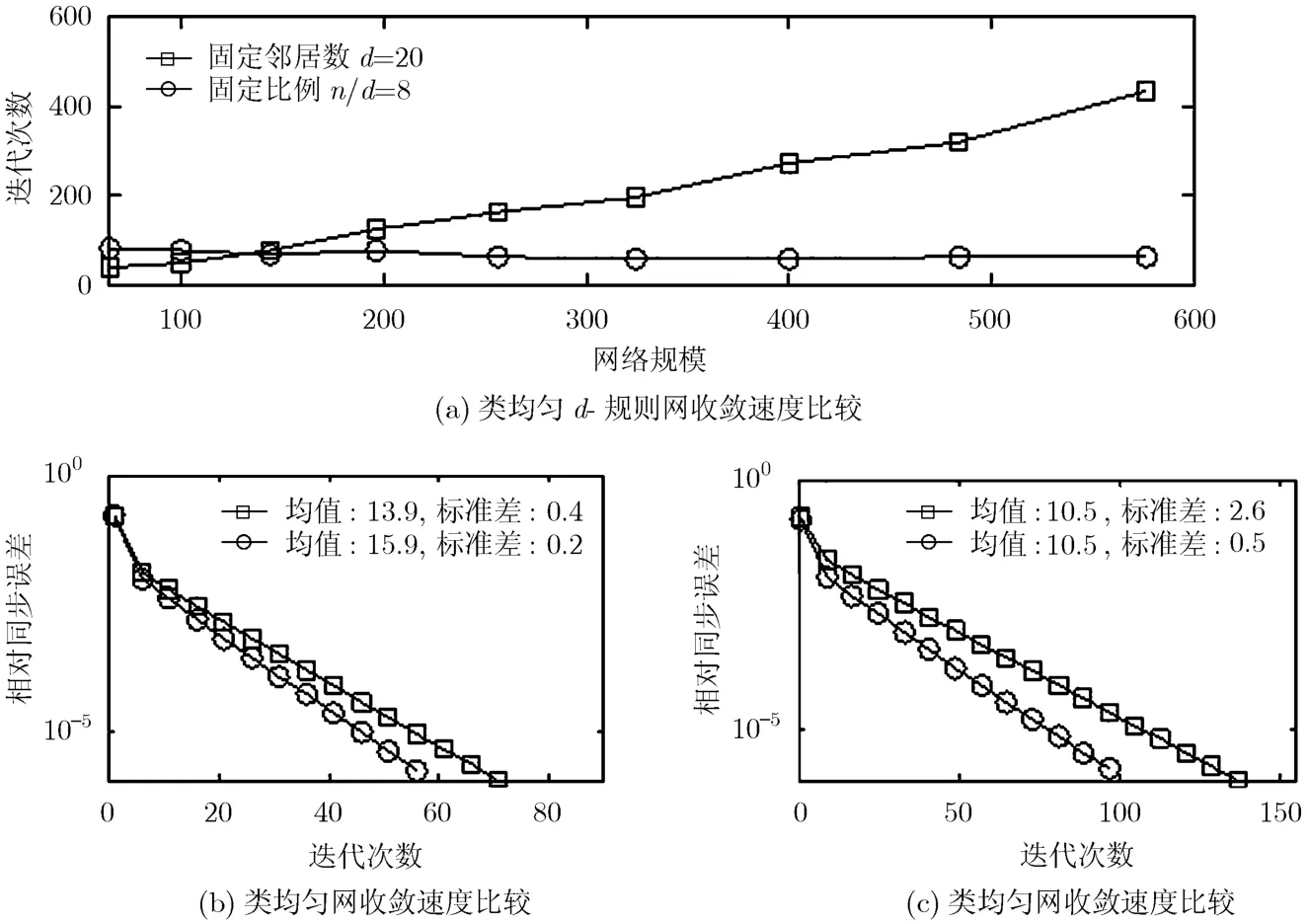
图3 收敛速度比较
分布式邻居数调整部分的目标是减小节点间邻居数的差异和增加网络的平均邻居数。前者是为了减少节点邻居数的差异对收敛速度的不利影响。算法1描述了一种分布式调整算法,可以在保持网络平均邻居数不变的情况下,减小网络中节点邻居数的差异。
算法1 DCTS的分布式邻居数调整算法1(DCTS-ACC1)
(1)所有节点设置周期性同步定时器和初始发射半径R;
(2)当节点vi的同步定时器被触发时,广播“同步请求消息”,设置同步应答定时器;
(3)接收到“同步请求信息”的节点vj回复“同步应答消息”,报告节点ID,时间信息tj和当前邻居数dj;
(4)节点vi接收“同步应答消息”,保存其中的ID信息,时间信息和邻居数信息。当同步应答定时器被触发时,
(a)基于式(1)调整本地时间信息ti;
(b)比较邻居节点的当前邻居数,找到最大和最小值dmax和dmin。若|dmax-dmin|≥Δ,执行步骤(c);否则不做邻居数调整;
(c)发送“邻居调整消息”给当前邻居数最大/最小的节点vmax/vmin,通知其减少/增加一个邻居节点。
(5)接收到“邻居调整消息”后,节点vmax/vmin查询邻居表,调整发射半径以减少/增加一个邻居节点。
算法1通过不断减小/增加邻居节点中的最大/最小邻居数,使不同节点的邻居数越来越接近,从而减小全网节点的邻居数差异。由于邻居数必须是整数,所以算法1不能保证各个节点的邻居数收敛到同一个值(这取决于网络调整前总的邻居数)。当本地邻居数之差小于给定阈值Δ时,就停止邻居数的调整。在算法1中,由于当某节点增加邻居时必有另一节点同时减少相等数目的邻居,所以网络总的邻居数和平均邻居数保持不变。
当邻居数分布的方差减小后,网络邻居数均值将决定DCTS的收敛速度。从加速算法收敛的角度出发,需要提高网络邻居数均值。算法2把节点的邻居数都增加到本地邻居数的最大值。通过迭代,节点的邻居数都收敛到网络调整前的最大邻居数。
算法2 DCTS的分布式邻居数调整算法2(DCTS-ACC2)
(1)所有节点设置周期性同步定时器和初始发射半径R;
(2)当节点vi的同步定时器被触发时,广播“同步请求消息”,设置同步应答定时器;
(3)接收到“同步请求信息”的节点vj回复“同步应答消息”,报告本地节点ID,时间信息tj和当前邻居数dj;
(4)节点vi接收“同步应答消息”,保存其中的ID信息,时间信息和邻居数信息。当同步应答定时器被触发时,
(a)基于式(1)调整本地时间信息ti;
(b)比较邻居节点的当前邻居数,找到最大值dmax。若当前邻居数di≠dmax,执行步骤(c);否则不做邻居数调整;
(c)查询邻居表,调整发射半径使邻居数达到dmax。
算法1仅减小了节点邻居数差异对DCTS收敛速度的影响,而算法2在消除了节点邻居数差异的同时还增加了邻居数均值,所以会有更好的加速效果。但是,算法1在增加部分节点发射半径的同时减小了另一部分节点的发射半径,而算法2则提高了网络中大部分节点的邻居数和发射半径,所以对网络平均发射半径和能耗的影响会大于算法1。
4.2 有效加速邻居比
由于邻居数调整算法的加速效果和网络平均发射半径及能耗互为制约,那么对于规模一定的类均匀规则网而言,是否存在较优的邻居数,能在有效加速DCTS收敛的同时也不过多地增加网络平均发射半径和能耗。
当循环网的规模一定时,由式(11)可知DCTS的收敛速度与邻居数成反比。也就是说,当邻居数较小时,增加它可以显著减少DCTS的收敛迭代次数;而随着邻居数的增加,迭代次数的减少速度开始变慢,此时再持续增加邻居数的加速效果不明显。
用加速阈值vthd表示当邻居数增加1时,DCTS所减少的收敛迭代次数。定义“有效加速邻居比”如下。
定义1 在规则网络中,有效加速邻居比feff为满足加速阈值vthd的最小邻居数和网络规模的比值。
令式(11)中迭代次数的下限为f(d),其关于邻居数d的一阶导数的绝对值为|f'(d)|=n/ d2。|f'(d)|反映了随着邻居数变化,循环网中DCTS收敛迭代次数下界的变化速度。当减少量开始少于阈值vthd时,当前的邻居数与网络规模的比就是有效加速邻居比的下界。同理可以得到有效加速邻居比的上界,如式(12)所示。
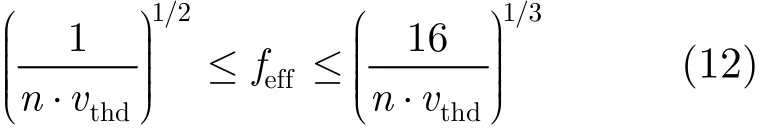
表1列出了当vthd为1和10时,不同规模循环网中有效加速邻居比的上下界和均值。当给定阈值时,随着网络规模增加,有效加速邻居比的上下界以及均值都呈下降趋势,且下降速度逐渐变慢。

表1 vthd=1,10时的有效加速邻居比的上、下界及均值
5 实验结果
为了验证本文提出的加速算法的加速效果,基于Matlab平台进行了网络仿真实验。相关参数设置如下:监测区域面积为100×100 m2,传感器节点构成类均匀网,网络规模为36-400,节点的初始传输半径为20 m。
5.1 DCTS加速算法在类均匀网中的加速效果对比
图4对比了当类均匀网的规模为100个节点时,初始和经过加速算法调整的DCTS的收敛速度。表2列出了加速调整前后网络邻居数分布的均值、标准差以及节点平均传输半径。其中,DCTS-ACC1算法的迭代次数约为调整前的75%,DCTS-ACC2的迭代次数约为调整前的50%。表2则表明,采用DCTS-ACC1算法时,网络的平均传输半径与调整前相当,而DCTS-ACC2由于增加了网络中大部分节点的传输半径,使全网平均发射半径比调整前增加了约24%。
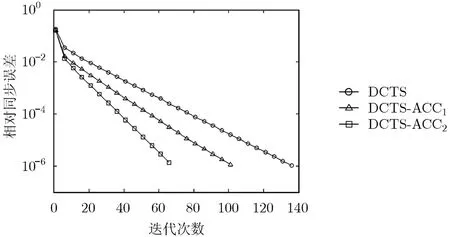
图4 收敛速度对比
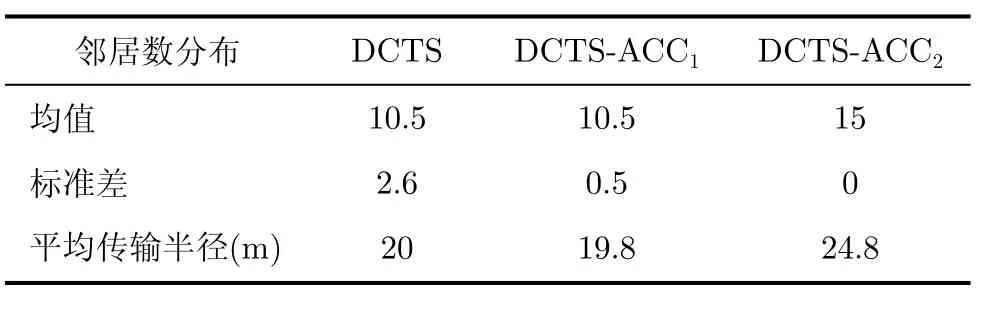
表2 加速调整前后的邻居数分布和平均传输半径
5.2 类均匀规则网的有效加速邻居比
图5(a)标出了在网络规模为400个节点的类均匀d-规则网中,对应于不同邻居数d,DCTS的收敛迭代次数。可以看出在网络规模固定时,随着邻居数d增加,收敛迭代次数的减少量呈先大后小的趋势,这与循环网的情况(式(11))一致。图5(b)标出了当速度阈值vthd分别取1和10时,不同规模类均匀规则网的有效加速邻居比。在两种阈值下的有效加速邻居比随网络规模变化的趋势都与循环网类似,即随着网络规模增加,有效加速邻居比逐渐减小并趋于稳定,大规模网络的有效加速邻居比趋于常数。
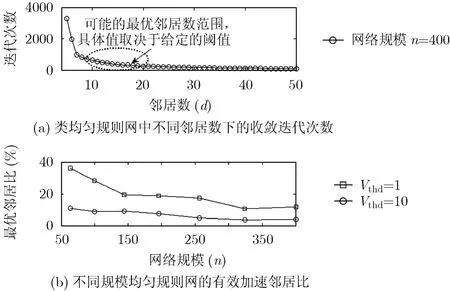
图5 有效加速邻居比
6 结束语
本文通过将DCTS迭代过程映射到马尔可夫链的状态转移过程,研究其收敛和加速问题。从分析和仿真结果可以看出,DCTS在循环网和类均匀规则网中的收敛速度与网络规模与邻居数的比值有关;而在类均匀网中,节点的邻居数分布也会影响DCTS的收敛速度。因此本文提出了通过调整节点邻居数分布来加速DCTS收敛的分布式算法。仿真结果表明该算法可以有效提高DCTS的收敛速度,在100个节点的类均匀网中,算法DCTS-ACC1在没有增加节点平均传输半径的情况下将DCTS收敛迭代次数减少了约25%。此外,为避免过度增加邻居数而消耗较多的传输能量,引入了“有效加速邻居比”以确定类均匀规则网的较优加速邻居数,并利用给定的速度阈值和网络规模推导出循环网有效加速邻居比的上下界。仿真结果表明,类均匀规则网的有效加速邻居比随网络规模的增加逐渐减小并趋于稳定,变化趋势类似于循环网。
[1] Ganeriwal S, Kumar R, and Srivastava M B. Timing-sync protocol for sensor networks. Proceedings of the First International Conference on Embedded Networked Sensor Systems, Los Angeles, CA, USA, 2003: 138-149.
[2] Sommer P and Wattenhofer R. Symmetric clock synchronization in sensor networks. ACM Workshop on Real-World Wireless Sensor Networks, Glasgow, Scotland,2008: 11-15.
[3] Giridhar A and Kumar P R. Distributed clock synchronization over wireless networks: algorithms and analysis. Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, USA, 2006: 4915-4920.
[4] Li Q, Rus D. Global clock synchronization in sensor networks.IEEE Transactions on Computers, 2006, 55(2): 214-226.
[5] Schenato L and Gamba G. A distributed consensus protocol for clock synchronization in wireless sensor network. 46th IEEE Conference on Decision and Control, New Orleans, LA,USA, 2007: 2289-2294.
[6] Gang X and Kishore S. Second order distributed consensus time synchronization algorithm for wireless sensor networks.Global Telecommunications Conference, IEEE, New Orleans,LA, USA, 2008: 1-5.
[7] Sommer P and Wattenhofer R. Gradient clock synchronization in wireless sensor networks. International Conference on Information Processing in Sensor Networks,San Francisco, USA, 2009: 37-48.
[8] Gang X and Kishore S. Performance of distributed consensus time synchronization with gaussian delay in wireless sensor networks. Wireless Communications and Networking Conference, IEEE, Budapest, Hungary, 2009: 1-5.
[9] Boyd S, Diaconis P, and Xiao L. Fastest mixing Markov chain on a graph. Siam Review, 2004, 46(4): 667-690.
[10] Kannan R. Markov chains and polynomial time algorithms.35th Annual Symposium on Foundations of Computer Science, Santa Fe, New Mexico, USA, 1994: 656-671.
