全数字接收机中一种基于并行流水线与快速FIR算法的插值滤波器结构及其实现

邓 军 杨银堂

①(西安电子科技大学微电子学院 西安 710071)

②(西安电子科技大学电子工程学院 西安 710071)

1 引言

在全数字接收机中，插值滤波器通过内插得到最佳采样值以实现码元同步的功能。插值滤波器性能的好坏直接影响到全数字接收机的误码率，设计性能良好的插值滤波器是设计全数字接收机的关键[1]。

插值滤波算法是一种数字信号处理方法，目前其实现大体有两种方法：软件方法和硬件方法。软件方法灵活性和移植性好，但是处理速度较慢、不够稳定。而硬件方法虽然在灵活性和移植性方面不及软件方法，但是硬件方法的处理速度快、稳定、效率高、集成度高。

当前国内外就全数字接收机中插值滤波算法实现的研究而言，普遍采用的是DSP软件实现，虽然Farrow提出了一种典型的易于硬件实现的Farrow结构[2]，但由于其运行速度较慢和功耗较高，对于64QAM，256QAM等高效调制信号未达到令人满意的效果。

本文把插值滤波算法映射到VLSI结构中，用以取代以前的DSP实现方法。在已有的拉格朗日立方插值滤波器Farrow结构基础上，首先，融入了流水线与并行处理技术来提高其运算速度、并降低功耗，但耗用资源较多。接下来，又在已得到的并行流水线Farrow结构的基础上，引入了快速FIR算法(FFAs)来生成复杂度降低的并行滤波结构。

通过仿真并在FPGA上实现，得到基于FFAs的结构在频率响应、脉冲响应及误码率性能上接近原结构，且与原结构相比，有着更快的运行速度和更低的功耗。

2 插值算法介绍

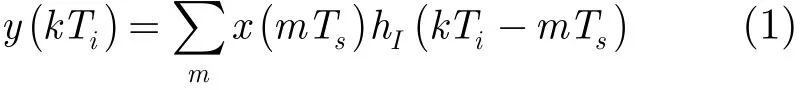
新的采样点就是最佳的插值点。只要将模拟滤波器hI(t)换成数字滤波器，就可以用数字的方法实现插值。定义基本指针mk=INT(kTi/ Ts)，分数间隔μk=kTi/ Ts−mk，滤波器指针i=INT(kTi/ Ts)−m=mk−m 则式(1)可改写为

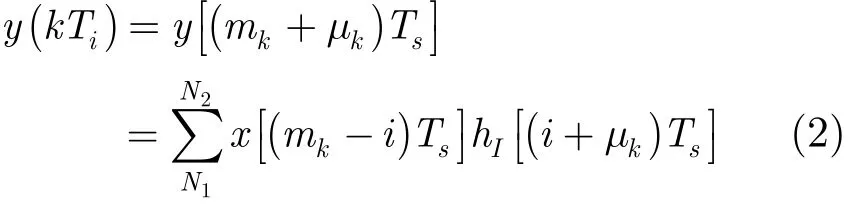
式(2)就是数字插值滤波器的基本方程。

常用的插值滤波器有线性插值滤波器、拉格朗日插值滤波器以及由最佳低通滤波器构成的性能优良的插值器。在本文中，主要研究的是拉格朗日立方插值滤波器。

下面给出了4抽头的拉格朗日立方插值滤波器的脉冲响应[1]

3 拉格朗日插值滤波器的Farrow实现结构

由于理想的sinc函数是不能物理实现的，于是就需要有一个能满足需要，并且易于硬件实现的内插函数。拉格朗日内插器较适合硬件实现[3]。Farrow提出了一种典型的易于硬件实现的完全计算式嵌套结构——Farrow结构。用Farrow结构设计拉格朗日多项式插值滤波器的原理如下：

插值滤波器是一种时变线性滤波器，冲激响应函数hI(i,μ)是内插估值点μ的函数，而μ是随时间变化的，所以冲激响应也是随时间变化的。对于这种带有可变因子的滤波器来说，可使用Farrow结构进行设计。下面用Farrow结构设计拉格朗日立方插值滤波器。

由式(1)可知冲激响应的系数分别为

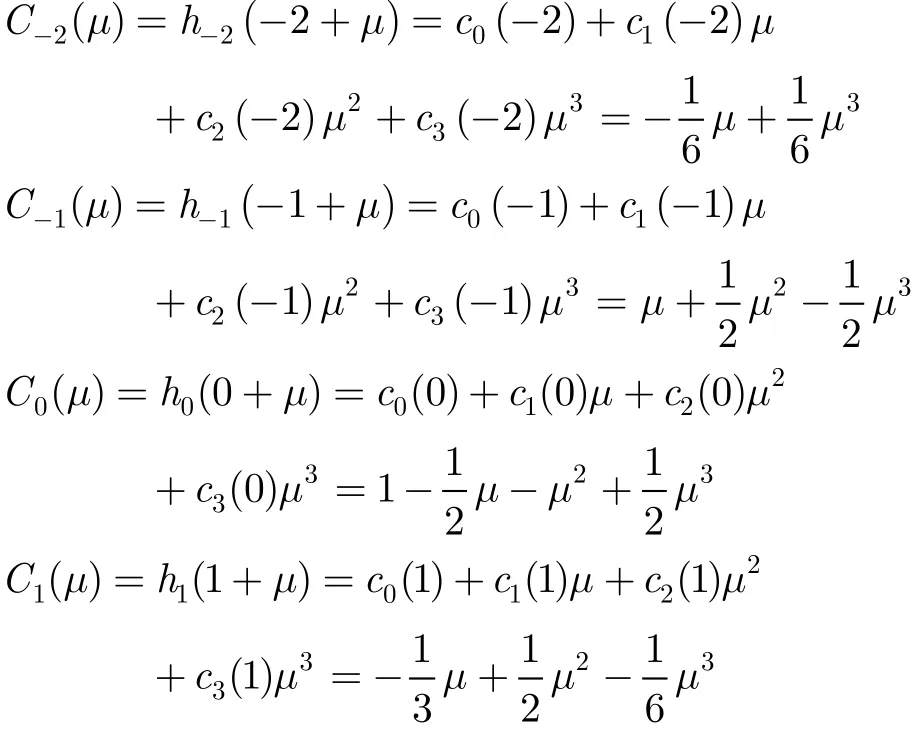
于是可得到插值滤波器的Farrow结构，图1给出了该滤波器的Farrow结构实现框图。可见，其关键路径为4TM+6TA。

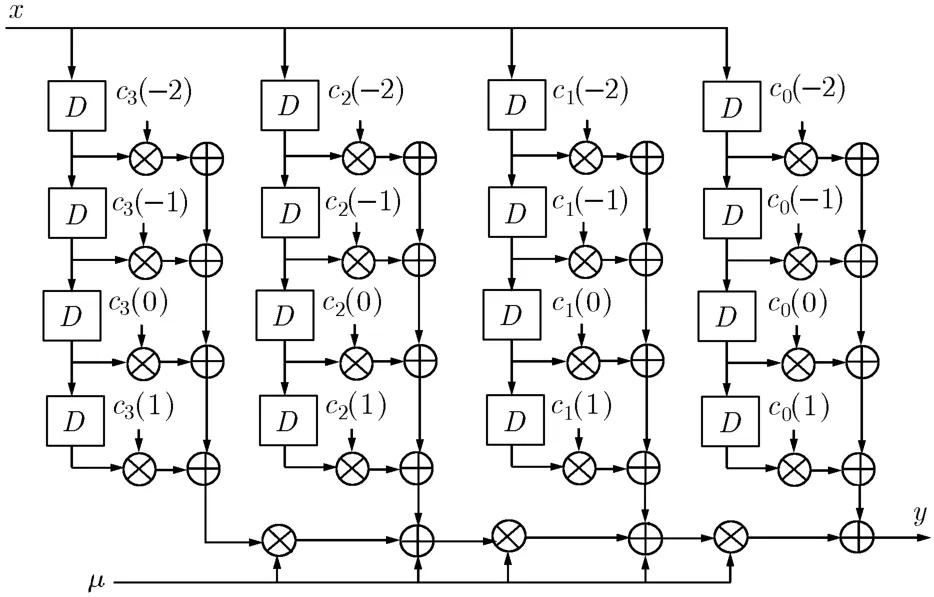
图1 拉格朗日立方插值滤波器的Farrow结构实现框图

4 基于并行流水线技术的Farrow结构

4.1 流水线技术应用

Merlino提到流水线是一种在程序执行时可以有多条指令重叠进行操作的并行处理实现技术，其导致了关键路径的缩短[4]，从而可以提高时钟速度或采样速度，或者可以在同样速度下降低功耗。关键路径的运算时间就是处理一个新样点所需要的最小时间。

笔者在文献[5]中提出的插入延迟单元后构成M级流水线系统，其关键路径缩短为原始路径长度的1/M，且电源电压可以降低到βV0(V0为原始电压)，其中β是一个小于1的常数。基于流水线技术的Farrow结构如图2。

从图2可以看见，这是一个3级流水线结构，关键路径由4TM+6TA减小到2TM+TA，速度相当于提高了1倍，当处理数据很多时，就节省了很多时间。功耗降低为原来的2β倍[5]。

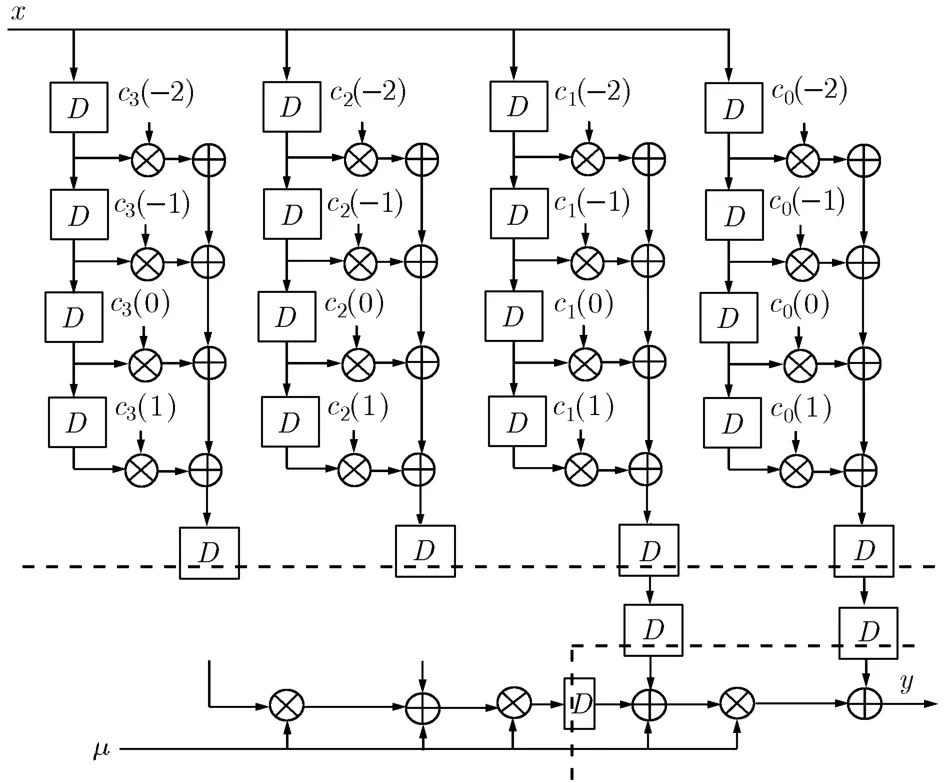
图2 流水线技术的插值滤波器Farrow结构实现框图

4.2 并行处理技术应用

并行处理涉及体系结构、算法映射、程序设计等多项技术，在VLSI数字信号的处理中，一直是个研究热点。在并行处理中，多个输出在一个时钟周期内并行地计算。这样，有效采样速度提高到与并行级数相当的倍数。并行处理和流水线一样，也能用来降低功耗[6,7]。

并行处理的功耗降低原理与流水线一样，通过降低电源电压来降低功耗。一个L路并行系统的功耗可降低为原来的β2倍[8]。即, β可通过下列二次方程求出：L(βV0−Vt)2=β(V0−Vt)2。

下面将并行处理加入到拉格朗日立方插值滤波器的Farrow结构中，如图3所示。

4.3 并行处理和流水线的结合应用

将流水线和并行处理技术加入到拉格朗日立方插值滤波器的Farrow结构(以2级并行流水线为例)如图4所示。

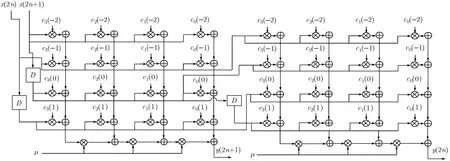
图3 并行拉格朗日立方插值滤波器的Farrow结构

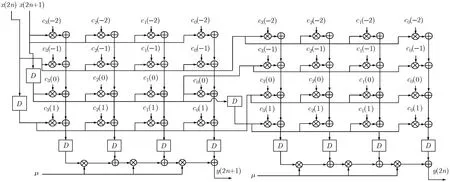
图4 2级并行流水线的拉格朗日立方插值滤波器Farrow结构图

2级并行流水线插值滤波器的Farrow结构与原始Farrow结构的比较见表1。

表1 2级并行流水线插值滤波器的Farrow结构与原始Farrow结构对比

由表可知道，相对于原始滤波器，2级并行流水线插值滤波器虽然使用的资源多了，但是速度提高成原来的(4TM+6TA)/(3TM+3TA)倍，功耗变成原来的β2倍[5]。

5 基于快速FIR算法的Farrow结构

由Winograd的著作[9]可知，2个L-1阶多项式相乘，可仅用2L-1个乘积项来实现。这种乘法数量的缩减是以加法数量的增加为代价来实现的。

一个被称为快速FIR算法(FFAs)的相对比较新型的算法就是依赖于这种方法生成复杂度降低的并行滤波结构[10]。采用这种方法，L并行滤波器可以近似用2L-1个长度为N/L的滤波运算来实现[11]。获得的并行滤波结构将需要2N-N/L次乘法。例如，如果设N=4，L=2，传统的2并行方法将需要8次乘法，而2并行快速滤波方法仅仅需要6次乘法。当N值很大时，FFAs可以大大缩减乘法的数量。

在时域，一个N抽头的FIR滤波器可表示为

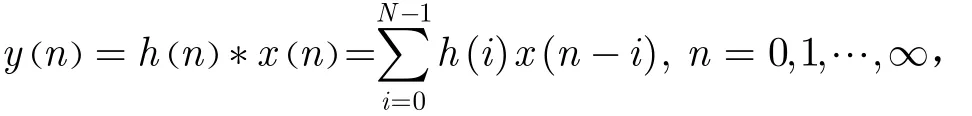
其中{x(n)}是一个无限长的输入序列，序列{h(n)}包含了长度为N的FIR滤波器的系数，或者可以在z域中可以表示为

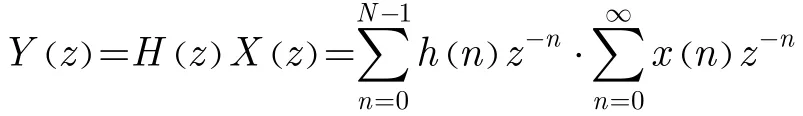
输入序列{x(0),x(1),x(2),…}可以被分解为偶数部分和奇数部分，如式(4)所示。

其中X0(z2)和X1(z2)分别为x(2k)和x(2k+1)(0≤k≤∞)的z变换。在式(4)中，X(z)被分解为两个多相式。同样，N长度的滤波器系数H(z)可以被分解为：H(z)=H0(z2)+z−1H1(z2)， 其中H0(z2)和H1(z2)长度分别为N/2，对应于偶数子滤波器和奇数子滤波器。偶数部分的输出序列y(2k)和奇数部分的输出序列y(2k+1) (0≤k≤∞)的计算如下式所示：

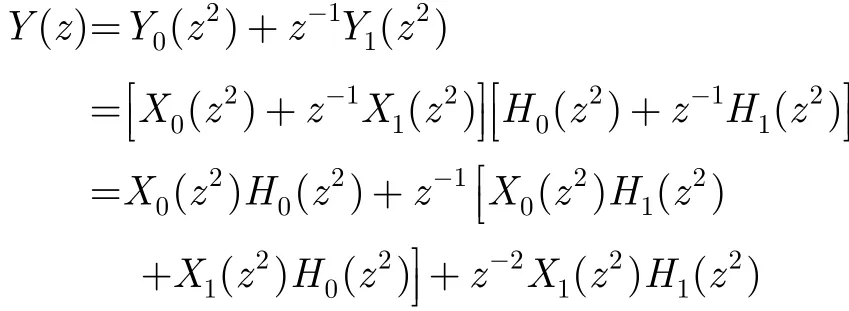
其中

Y0(z2)和Y1(z2)分别对应时域里的y(2k)和y(2k+1)。式(5)和式(6)中的滤波运算在每次迭代中，处理两个输入x(2k)和x(2k+1)，并产生两个输出y(2k)和y(2k+1)，所以被称为2并行FIR滤波器。这个2并行FIR滤波器可用矩阵形式表示如下：

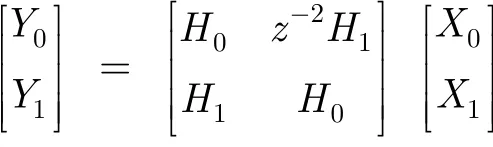
式(5)和式(6)所展示的2并行FIR滤波器需要2N次乘法和加法运算。可将它们看写成下面的形式：

这个2并行快速滤波器包括5个子滤波器；然而其中的H0X0和H1X1是公共项，在计算Y0和Y1时可以共用。

根据式(7)和式(8)可得到基于快速FIR算法的拉格朗日立方插值滤波器Farrow结构，如图5所示。

通过这种方法可得到许多等价的并行FIR滤波器结构，这些结构都是等价的。但是，这些滤波器在硬件VLSI实现中，它们的性能却有很大的差别。例如，在一个窄带低通滤波器中，子滤波器H0+H1可能需要比H0−H1更多的非零比特[9]。值得注意的是系数的和或者差也可以用于缩减序列滤波器的强度。另外，不同结构也将导致不同的舍入噪声特性。选择合适的滤波器结构也可以减小舍入噪声。

Farrow结构插值滤波器的快速FIR算法与图5所示的2级并行处理立方插值滤波器的Farrow结构的比较见表2。

由表可知，使用快速FIR算法比2级并行流线使用更少的资源。

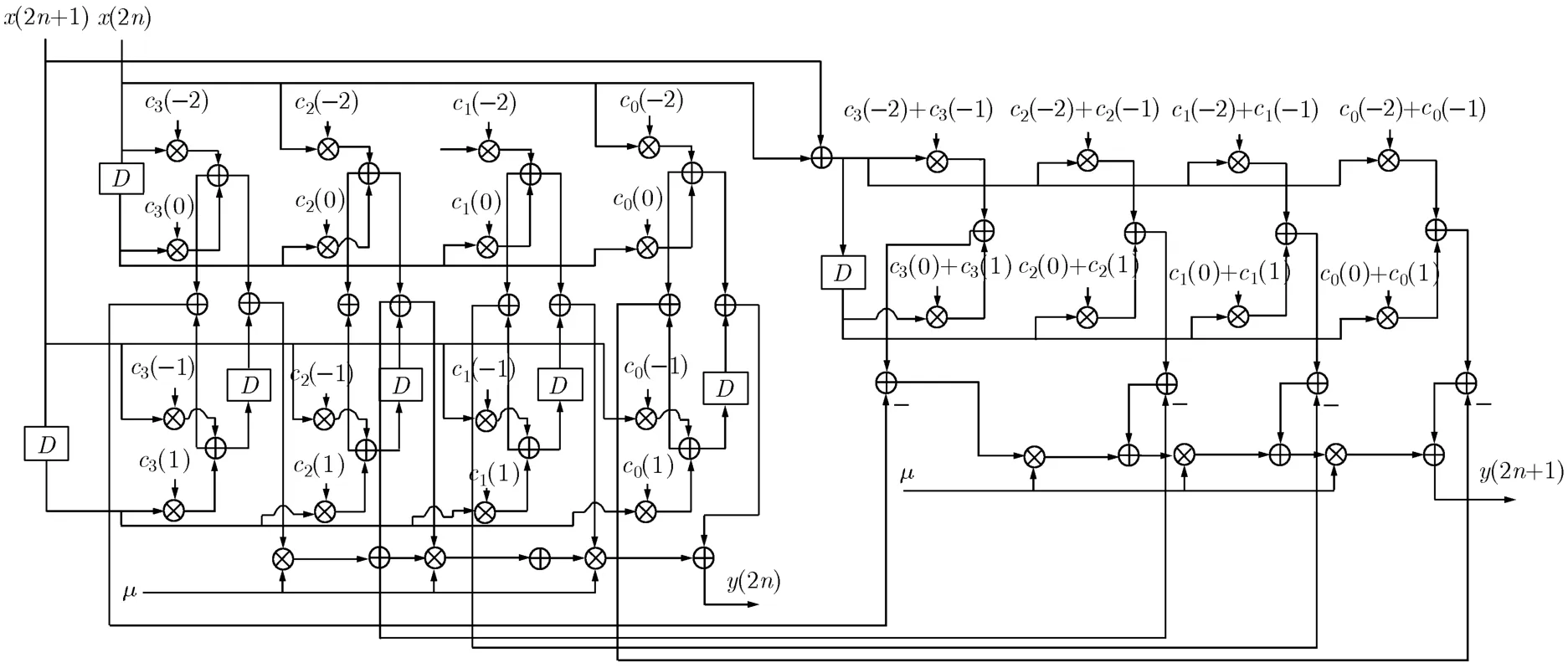
图5 基于快速FIR算法的拉格朗日立方插值滤波器Farrow结构图

表2 快速FIR算法与2级并行流水线的比较

6 仿真结果分析及实现

以2倍符号速率对接收到的4QAM调制信号进行采样，求出时钟误差后分别用原始Farrow结构立方插值法和基于FFAs的Farrow结构插值法对采样序列进行的插值滤波绘出插值滤波器输出信号星座如图6。显然图6(a)中所示原始Farrow结构得到的星座信号点与图6(b)中基于FFAs的Farrow结构得到的星座信号点基本一致。

另外，我们还通过误码率性能考查了原始Farrow结构立方插值滤波器和基于FFAs的Farrow结构插值滤波器的滤波性能。以16QAM信号为例，采样速率为4倍的符号速率，系统脉冲响应取滚降因子为0.5的升余弦脉冲函数。上述两种滤波器插值滤波后的误码率对比图如图7所示。可以看出，基于FFAs的Farrow结构插值滤波器与了原始Farrow结构的插值滤波器的误码率基本一致。

最后，我们对基于FFAs的Farrow结构的插值滤波器进行了Verlog HDL编程，并在Actel的FPGA(A3P030)上下载成功。图8为仿真波形，仿真中只研究编程的正确性，故假设μ=1。由图中可以看出，输出的结果符合希望所得到的结果。

7 结束语

本文对拉格朗日立方插值滤波器的Farrow结构进行研究，在Farrow结构的基础上，加进流水线、并行处理等技术，并利用FFAs算法对该结构进行改进。对改进的结构进行仿真并与原始结构进行比较。对原始的Farrow结构加入流水线与并行处理技术后，关键路径减少，运行速度提高，功耗降低，且星座信号点的收敛性和误码性能与原结构基本一致；但耗用的资源却增加，将加大专用集成芯片的面积。而基于快速FIR算法的改进比并行流水线结构要节省一些资源，同时也提高了运行速度，降低了功耗。

图6 原始Farrow结构和基于FFAs的Farrow结构得到的星座信号点对比图

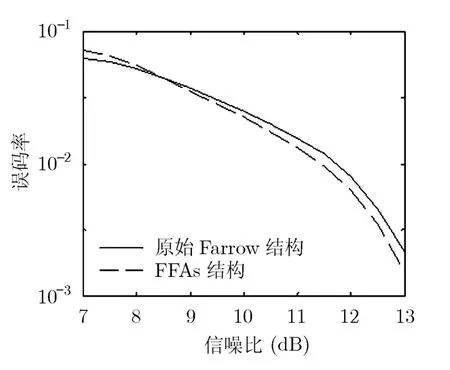
图7 16QAM的两种结构的 插值滤波器误码性能对比图

图8 FFAs的Farrow结构的仿真波形图

[1] 张公礼. 全数字接收机理论与技术[M]. 北京：科学出版社，2005年1月: 61-85.Zhang Gong-Li. Theory and Technology of All Digital Receiver[M]. Beijing: Science Press, 2005: 61-85.

[2] Gardner F M. Interpolation in digital modems part I:fundamentals[J]. IEEE Transactions on Communications,1993, 41(3): 501-507.

[3] Erup L, Gardner F M, and Harris R A. Interpolation in digital modems part II: implementation and performance[J].IEEE Transactions on Communications, 1993, 41(6):1135-1141.

[4] Merlino P and Abramo A. A fully pipelined architecture for the LOCO-I compression algorithm[J]. IEEE Transactions on Very Large Scale Integration Systems, 2009, 17(7): 967-971.

[5] 邓军, 杨银堂. 全数字接收机中一种低功耗插值滤波器结构及其VLSI实现[J]. 西安电子科技大学学报, 2010, 37(2):320-325.Deng Jun and Yang Yin-tang. A structure of low-power interpolation filter and its VLSI implementation for all digital receiver[J]. Journal of Xidian University, 2010, 37(2):320-325.

[6] Tawfik S A and Ursun V K. Low power and high speed multi threshold voltage interface circuits[J]. IEEE Transactions on Very Large Scale Integration Systems, 2009, 17(5): 638-645.

[7] Tam W P, Lok T M, and Wong T F. Flow optimization in parallel relay netwoks with cooperative relaying[J]. IEEE Transactions on Wireless Communications, 2009, 8(1):278-287.

[8] Polpo A and Pereira C A B. Reliability nonparametric Bayesian estimation in parallel system[J]. IEEE Transactions on Reliability, 2009, 58(2): 364-373.

[9] Winograd S. Arithmetic complexity of computations.CBMS-NSF Regional Conference Series in Applied Mathematics, SIAM Publications, 1980, 33: 21-33.

[10] Parker D A and Parhi K K. Low-area/power parallel FIR digital filter implementations[J]. Journal of VLSI Signal Processing, 1997, 2(1): 75-92.

[11] Jain V and Blair W D. Filter design for steady-state tracking of maneuvering targets with LFM waveforms[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009,45(2): 765-772.