正则形理论在交直流互联电力系统稳定性分析中的应用
2010-03-27万家晶
万家晶, 肖 锐
(1.东北电力大学电气学院,吉林吉林 132012; 2.大庆石油管理局供水公司,黑龙江大庆 163458)
0 引 言
随着电力电子技术、计算机技术的发展,高压直流输电也得到了飞速的发展,已在远距离大容量输电、海底电缆输电和不同频率或相同频率交流系统之间的非同步联网等方面表现出较大的优势。与交流系统相比,直流输电在经济上具有线路造价低、年电能损失小的优点,在技术上具有远距离大容量输电、非同步联络能力、网损小、功率控制灵活等优点。我国目前进入了从大区性电网向全国交直流互联电网的过渡阶段[1-2]。
全国联网在带来巨大联网效益的同时,也给电力系统运行带来一些新的挑战:由于直流系统的投运,使电力系统的非线性进一步复杂化,其中任一元件故障都有可能会导致系统性能的下降,严重威胁到系统的安全稳定运行,因此,必须对交直流系统大干扰后的动态行为进行分析。传统上对于电力系统大干扰稳定性分析无一例外地采用时域仿真法和暂态能量函数法,而前者不能给出系统的频域信息,后者对系统稳定性分析也存在很大的误差。正则形[3-8]系统的非线性特性,通过坐标变换使原系统与一个线性系统二阶或更高阶等价。将正则形理论应用到电力系统的稳定性分析中,既保留了以上两种方法的优点,又考虑了模式间的非线性作用,适用于大干扰后系统的动态行为分析和稳定性的判断。现将正则形理论应用到一个简单的三机交直流互联电力系统,对交直流输电系统非线性稳定因子进行分析,得出新的结论。
1 交直流系统数学模型
建立全系统模型时,首先将整个交直流系统分成直流系统和交流系统两部分,然后分别进行建模,再通过AC/DC接口方程将这两个系统模型联立起来,从而建立了全系统的数学模型。
1.1 交流系统数学模型
发电机模型采用经典二阶模型,其动态方程为:

式中:Pmi——机械功率;
Pei——电磁功率;
Ti——发电机惯性时间常数;
ωi——角速度;
δi——角变量;
Di——阻尼系数。
ω0=314 r/s,状态变量为[ωi,δi],中间变量为Pei。
1.2 直流系统数学模型
直流系统数学模型包括换流器模型、直流输电线路模型和控制器模型。
由整流器、逆变器及直流输电线路构成的双端直流系统的单线图如图1所示。
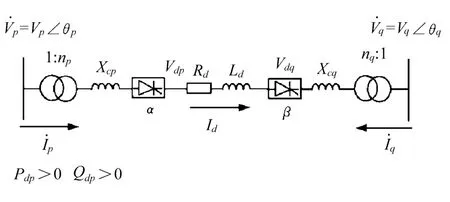
图1 双端直流输电系统单线图

而对于逆变器,直流电压方程应为:

其中,直流线路运动方程为:
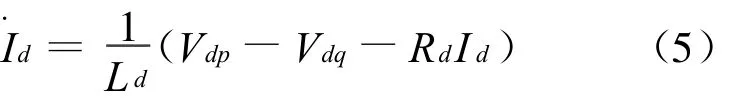
对于控制器,在这里整流侧采用定电流控制,逆变侧采用定电压控制,则控制器数学模型为:

式中:uα——整流侧控制信号;
Vdq0——逆变侧空载直流电压;
α0,β0——整流器和逆变器触发滞后、超前角的给定值。
1.3 AC/DC接口方程

其中

将式(4)与式(7)联立,则得到以Vp,θp,Vq,θq为变量的接口方程:
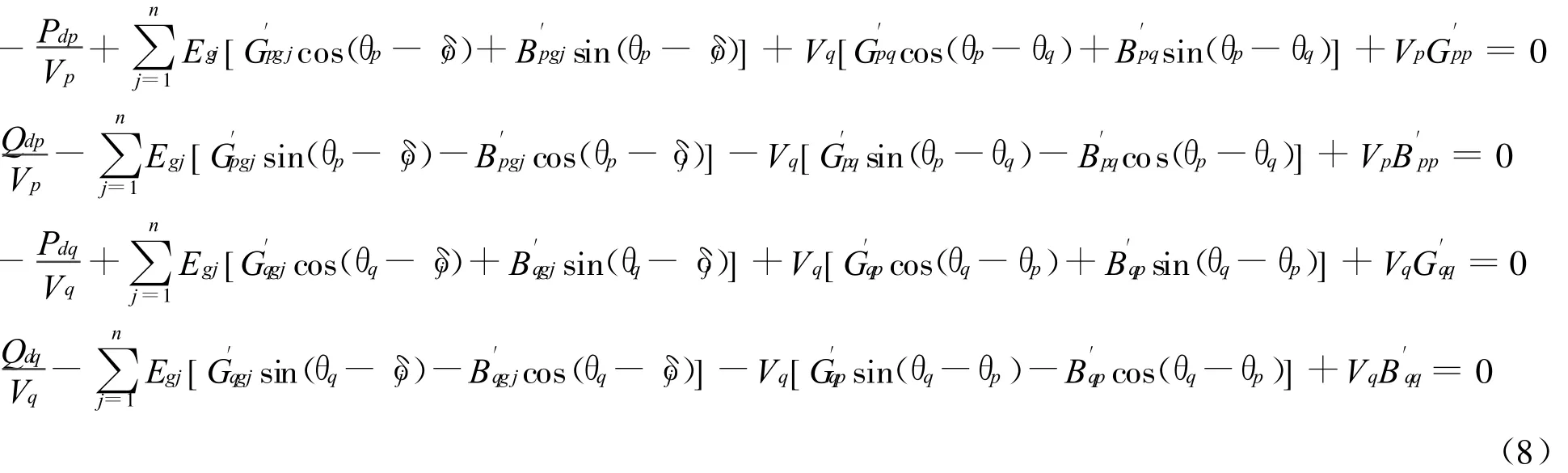
由于式(8)中存在三角函数,计算起来比较困难,因此必须消去三角函数项,在这里对其进行泰勒级数展开至二阶项,根据sinx=x,cosx=1-,可以得到以上三角函数的二阶展开式,从而使式子简化。
1.4 发电机的电磁功率

根据式(1)~式(9),从而得到以[δ,ω,Id,α,β]为状态变量的全系统数学模型的表达式为:

2 正则形非线性稳定因子
2.1 稳定因子的提出

首先将其进行线性变换X=UY,展开可得:
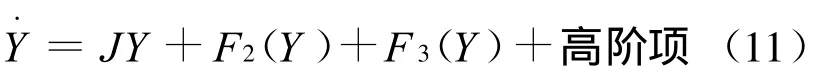
当系统不发生二阶共振时,再对其进行二阶非线性变换Y=Z+h2(Z),在Z非常小的情况下有:
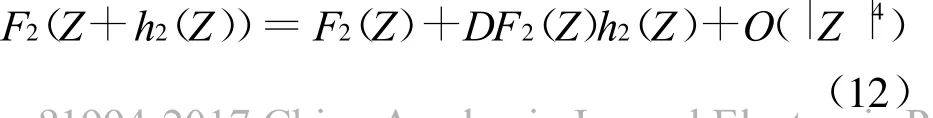
将Y=Z+h2(Z)代入式(11),再利用式(12)可以得到:

令系统的第i个模式λi=αi+jβi,则有:

根据式(13)有:



当仅考虑第i个模式时,式(17)可写成:

对式(18)求微分方程有:

2.2 稳定因子的分析
2.2.1 阻尼因子aij
1)模式i受模式j幅值变化影响的一个物理量,当|aij|越大,模式i的幅值变化的将越快。
2)aij是正则形变化过程中省略的三阶交叉项的系数,它描述了模式间的非线性相互作用。
2.2.2 稳定域因子Ri
若式(18)中只有第i个模式幅值存在,其它幅值近似为0时,也就是说,模式间的相互作用较弱时,此时第i个模式的幅值被定义为Ri:

3 算例分析
三机交直流互联电力系统如图2所示。

图2 三机交直流互联电力系统
发电机采用经典二阶模型(δ,ω),高压直流系统采用准稳态模型,额定电压为500 kV,单极单桥,额定容量为800 MW,整流侧采用定电流控制,逆变侧采用定电压控制,在E点发生三相接地短路瞬时故障,tc时刻故障清除。系统中具体参数如下:

3.1 低频振荡模式求取
以一号机为参考机,状态变量为[δ21,δ31,ω1,ω2,ω3,Id,α,β],利用仿真计算,求出系统的特征根及左右特征向量。系统中共有8个特征值,见表1。

表1 三机交直流互联系统特征值
利用线性相关因子公式 pki=uki×vki,根据已求出的系统左右特征向量,可以求出系统中单个模式的线性相关因子,见表2。
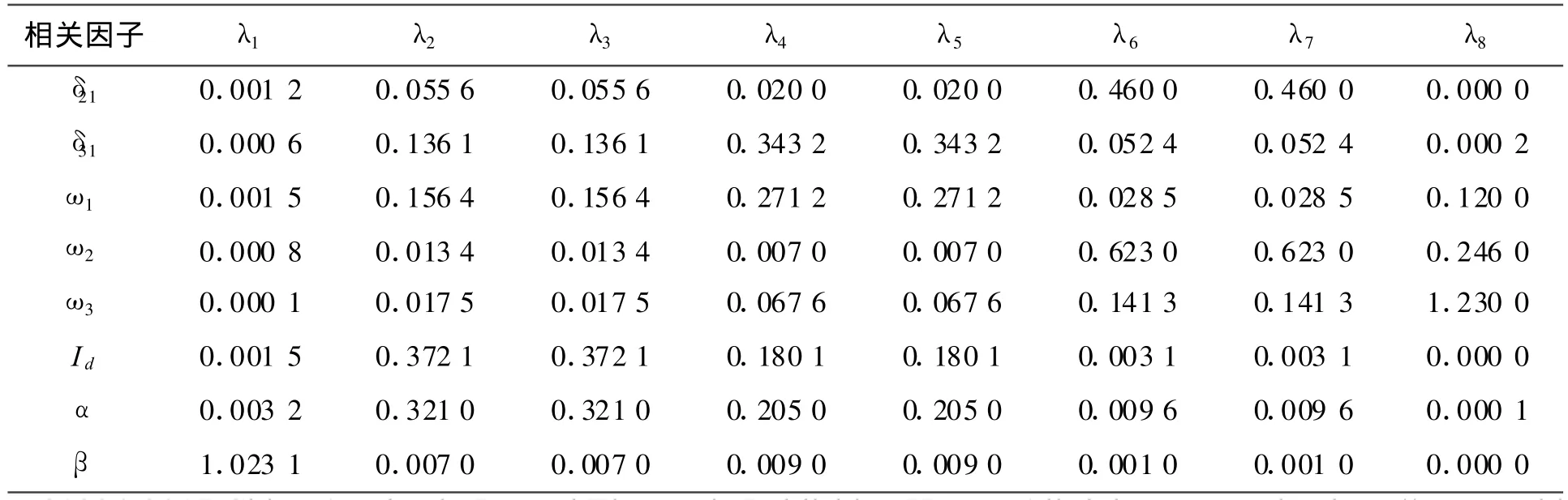
表2 系统中线性相关因子
低频振荡模式判断依据:
1)机电回路相关比:
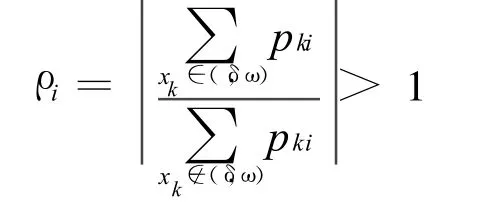
2)特征根 λi=αi+jβi,频率范围为0.2~2.5 Hz。
必须满足以上两个条件才属于低频振荡模式。
依据此可以判断出λ4,5,λ2,3,λ6,7对应的频率和机电回路相关比,见表3。
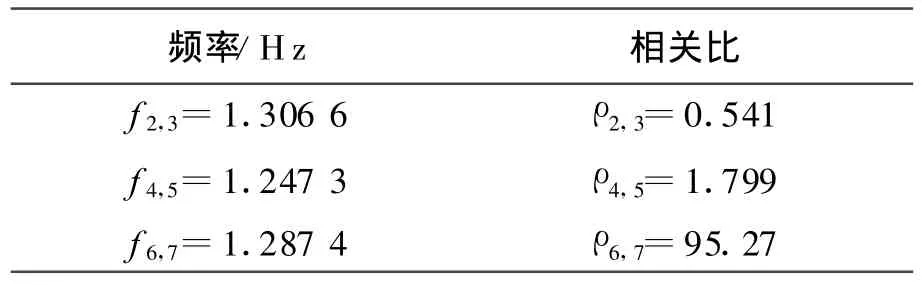
表3 对应的频率和机电回路相关比
由此可以判断出特征值λ4,5,λ6,7是系统低频振荡模式。
从表2可以看出,模式4与状态变量δ31最强相关,次之是 ω1,由此可知模式4应是发电机1与发电机3之间的局部振荡模式;模式6与状态变量ω2最强相关,次之是δ21,可知模式6是发电机1与发电机2之间的局部振荡模式;模式2与变量Id强相关,次之是α,所以属于控制模式。
3.2 非线性稳定因子的求取
为了方便,在这里只对λ4,λ6两个低频振荡模式进行分析,根据式(16)和式(20)对aij和Ri进行求取,结果见表4和表5。
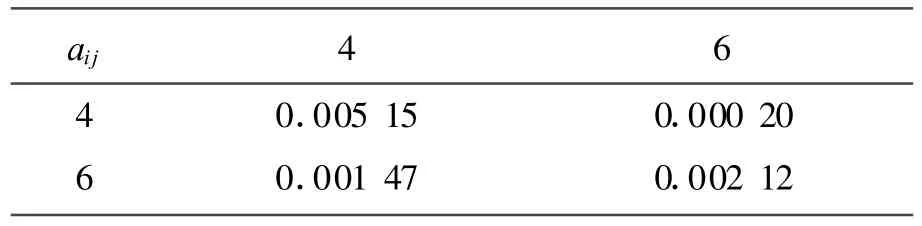
表4 阻尼因子aij

表5 稳定域因子Ri
由表4可以看出,aij均为正数,所以模式4和模式6的幅值将衰减的越来越慢,而且a4,4最大,说明模式4的幅值衰减的最慢。
由表5可以看出,由于R4<R6,说明模式4比模式6更容易失稳。随着tc的增大,如果r4>R4或r6>R6时,系统将不稳定。
3.3 时域仿真
为了对上述计算及分析的有效性和正确性进行验证,在此进行时域仿真模拟,如图3所示。

图3 模式4和模式6的幅值振荡曲线
由图3(a)可以看出,在小干扰情况下,模式4和模式6都是稳定的,且模式4比模式6更加稳定。
由图3(b)可以看出,当系统处于临界稳定时,模式4的衰减变弱,无法判断哪个模式更加稳定。
由图3(c)可以看出,模式4的幅值不断地增加,此时系统失去稳定。
时域模拟验证了非线性稳定因子的有效性及正确性。
4 结 语
当系统受到大扰动后,用以往的分析法对系统的稳定性判断极其困难。对三机交直流电力系统进行分析,结果显示,正则形非线性稳定因子的方法可以有效地判断出系统的稳定区域,并判断出系统的稳定性,仿真结果验证了此法的有效性和正确性。
[1] 曾德文.全国电力系统联网的基本格局及其分析[J].中国电力,1999,2(10):29-30.
[2] 徐政.交直流电力系统动态行为分析[M].北京:机械工业出版社,2004.
[3] 黄莹.交直流电力系统动态特性分析方法研究[D]: [博士学位论文].杭州:浙江大学,2005.
[4] Y X Ni,V Vittal.Nonlinear modal interaction in HVDC/AC power systems with DC power modulation[J].IEEE Transactions on Power Systems,1996,11(4):2011-2017.
[5] R J Betancourt,E Barocio.A real normal form approach to the study of resonan power systems[J]. IEEE Transactions on Power Systems,2006,21(1): 431-432.
[6] 邓集祥,华瑶,张芳.振荡模式非线性相关作用的研究[J].电力系统自动化,2003,27(16):35-39.
[7] 邓集祥,涂进,陈武晖.大干扰主导低频振荡的鉴别[J].电网技术,2007,31(7):36-41.
[8] 邓集祥,姜涛.基于正则形理论的电力系统增幅低频振荡研究[D]:[硕士学位论文].吉林:东北电力大学,2009.
