聚焦变换在MIMO阵列方位估计中的应用
2010-03-24
(海军装备部,西安 710043)
0 引言
多输入多输出(Multiple-Input Multiple-Output,MIMO)阵列是近年来信号处理领域提出的一种新体制阵列技术[1],在雷达和声纳研究方面具有广阔的应用前景。MIMO阵列通过多个阵元同时发射独立信号,并利用多个阵元接收目标的反射信号,从而获得目标检测与参数估计增益。MIMO阵列技术分为两类:第一类利用大物理间隔的发射和接收阵列所产生信号的差异性得到空域分集增益,可以有效抑制目标闪烁[2];第二类是与传统阵列类似的收发合置阵列,利用各阵元发射信号的独立性,可以获得相互独立的目标观测回波,从而避免了常规阵列中的相干源问题[3]。
MIMO阵列的方位估计方法研究一直是MIMO技术的研究重点。文献[4]提出了基于迭代广义似然率测试的信号检测和最大似然方位估计方法。文献[5]给出了基于MIMO阵列的最小方差方位估计方法。文献[6]对自适应波束形成方法应用于MIMO阵列的问题进行了研究。文献[7]将 MUSIC方法在MIMO阵列和常规相控阵中的性能进行了比较。然而,上述研究均未考虑信号带宽带来的方位估计误差,直接进行高分辨方位估计会造成因信号频率不同带来的方位估计模糊。
本文将聚焦变换应用于MIMO阵列的方位估计,提出了一种基于聚焦变换的MIMO阵列方位估计方法,利用聚焦变换将多个相互独立的回波信号投影到一个信号空间,从而显著提高了目标方位估计的分辨能力和精度。
1 MIMO阵列的信号模型
考虑由M个全向阵元组成收发合置的均匀线阵列,P个目标处在阵列的远场,各发射阵元发射相互独立的窄带信号,第m个阵元的发射信号表示为sm(t)。假定噪声为与信号不相干的加性白噪声,则第n个阵元接收到的信号表示为

式中:fm表示第m个发射阵元的信号载频;εn(t)表示第n个接收阵元的噪声;τmn(θ)表示阵元m 发射信号经目标反射到达n 阵元相对于参考阵元的时延;θp表示目标p的入射方位。
令

式中:am(θ)和b(θn)分别表示第m个发射阵元和第n个接收阵元的方向矢量。
阵列的发射信号向量表示为

发射阵列的方向矢量表示为

接收阵列的方向矢量表示为

则MIMO阵列的输出向量表示为

2 聚焦算法
由于MIMO阵列发射多个不相干的单频信号,MIMO阵列的方位估计实际上可近似为宽带信号处理问题[8]。宽带信号的高分辨方位估计一般采取基于频带分解的子空间方法,即将宽带信号分解为多个窄带,然后对每个窄带进行高分辨方位估计。对于相干目标来说,上述方法将由于目标回波相干而失效。Wang H 等人提出的宽带聚焦方法将不同频率的多个窄带信号通过聚焦变换到同一信号子空间,可以有效利用带宽内的信号能量,提高方位估计的性能,其本质是聚焦矩阵的选择。
CSM(coherent signal-subspace method)[9]和RSS(rotational signal-subspace)[10]等方法构造聚焦矩阵时需要目标方位的预估值,显然不适用于宽带信号的方位估计。
文献[11]提出了不需要方位预估的双边变换TCT(two-sided correlation transformation)方法。
双边相干变换TCT算法是利用各频率点间无噪声数据之间的关系来构造聚焦矩阵T,将频率 fj处的无噪协方差矩阵变换到频率 f0处,描述为约束最优化问题为:

求解上式可得最小范数解为:

式中:U (f0)、U (fj)分别是PS(f0)、PS(fj)的特征向量矩阵。
由信号模型可知,
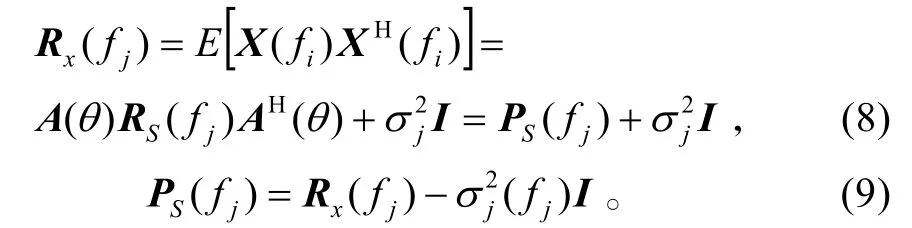
在实际应用中,通过下面两式得到 RX(fj)和的估计值:
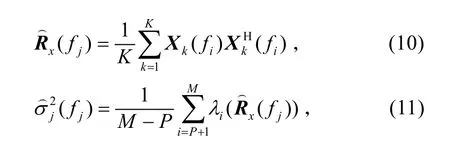
式中:iλ为协方差矩阵降序排列的特征值;k是快拍数。
3 基于聚焦变换的MIMO阵列DOA方法
通过分析MIMO阵列的信号模型,MIMO阵列的方位估计近似为一个宽带信号方位估计问题。由于MIMO阵列发射信号的相互独立性,可以通过滤波或相关等方法将各个频率分量的接收信号分离出来[7]。继而采用宽带TCT 聚焦算法,将MIMO阵列的多个频率分量信号聚焦到同一个频率上,再进行高分辨方位估计,从而利用MIMO阵列的不相干回波和宽带信号能量聚焦提高了方位估计性能。
综上所述,基于聚焦变换的MIMO阵列方位估计方法的具体步骤为:
Step 1:对MIMO阵列接收信号进行匹配滤波,得到多个独立频率分量的信号;
Step 2:对频率分量 j=1,2,…,J,根据式(10)和(11)得到协方差矩阵和噪声方差的估计值,进而由式(9)得到无噪声协方差矩阵的估计值;
Step 3:由式(7)求得聚焦矩阵 T (fj);
4 仿真实验验证
仿真采用收发合置的五元均匀线列阵,发射5路单频正交信号,信号的频带为3~7 kHz,阵元间距为信号中心频率的半波长,3个远场相干信号源分别从9°、12°、20°入射。本文提出的聚焦高分辨方位估计算法(FT-MUSIC)与MIMO阵列直接采用MUSIC算法作比较分析。
信噪比为5 dB时,F-MUSIC 和MUSIC 对3个目标方位估计的空间谱如图1所示。由图1可看出FT-MUSIC算法明显提高了MIMO阵列的目标分辨能力。仿真条件不变,信噪比从−10~20 dB 变化时,对每个信噪比做200次蒙特卡罗实验。FT-MUSIC和MUSIC 对3个目标方位估计的均方误差如图2~4所示。统计性能可以看出,本文提出的方法在目标估计精度上优于MIMO阵列直接采用MUSIC算法。
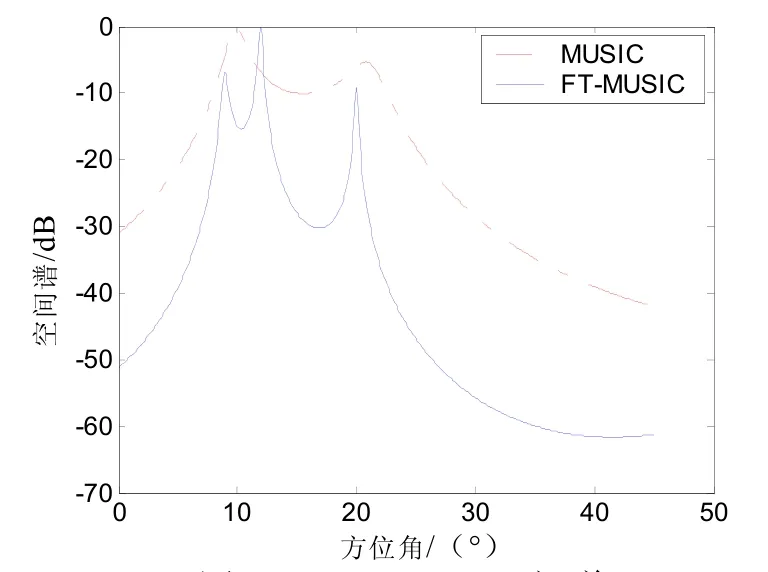
图1 3个目标的空间谱

图2 目标1的估计均方误差

图3 目标2的估计均方误差

图4 目标3的估计均方误差
5 结论
本文通过分析 MIMO阵列的信号模型,将MIMO阵列方位估计近似为常规宽带信号方位估计问题,并提出了基于TCT 聚焦变换的MIMO阵列方位估计算法,利用MIMO阵列的不相干回波和宽带信号能量聚焦提高了MIMO阵列的方位估计性能。最后通过仿真验证了该方法的有效性,估计精度高于MUSIC算法直接对MIMO阵列方位估计。
[1]JIAN LI,PETRE STOICA.MIMO radar with colocated antennas[J].IEEE SIGNAL PROCESSING MAGAZINE,2007,24(5):106-114.
[2]FISHLER E,HAIMOVICH A,BLUM R,et al.MIMO radar:an idea whose time has come[C]//Proc.IEEE Radar Conf.2004:71-78.
[3]TABRIKIAN J,BEKKERMAN I.Transmission diversity smoothing for multi-target localization[C]//IEEE International Conference on Acoustics,Speech,and Signal Processing (ICASSP’05).Philadelphia,PA,USA,2005:1041-1044.
[4]BEKKERMAN I,TABRIKIAN J.Target detection and localization using MIMO radars and sonars[J].IEEE Trans.Signal Processing,2006,54(10):3873-3882.
[5]LUZHOU X,JIAN L.Iterative generalized-likelihood ratio test for MIMO radar[J].IEEE Trans.Signal Processing,2007,55(6):2375-2385.
[6]XU L,LI J,STOICA P.Adaptive techniques for MIMO radar[C]//Proc.4th IEEE Workshop on Sensor Array and Multi-channel Processing.Waltham,MA,2006:258-262.
[7]WILCOX D,SELLATHURAI M,RATNARAJAH T.A comparison of MIMO and phased array radar with the application of MUSIC[C]//Proc.IEEE Fortieth Annual Asilomar conference on Signals,Systems,and Computers.Pacific Grove,California,2007:1529-1533.
[8]熊波,李国林,尚雅玲,等.信号相关性与DOA 估计[J].电子科技大学学报,2007,36(5):907-910.
[9]WANG H,KAVEH M.Coherent signal subspace processing for the detection and estimation of multiple wideband sources[J].IEEE Trans.on Acoustics,Speech,and Signal Processing,1985,33(4):823-831.
[10]HUNG H,KAVEH M.Focusing matrices for coherent signal sub-space processing[J].IEEE Trans.on Acoustics,Speech,and Signal Processing,1988,36(8):1272-1281.
[11]VALAEE S,KABAL P.Wideband array processing using a two-sided correlation transformation[J].IEEE Trans.on Signal Processing,1995,43(1):160-172.
