反舰导弹末端蛇行机动突防效果仿真

毕兰金，李耀阳，武志东

（1.海军航空工程学院 控制工程系，山东 烟台 264001；2.海军驻航天一院军事代表室，北京 100076）

现代海战中，反舰导弹是攻击对方大中型水面舰艇的主要武器。通常情况下，大中型水面舰艇都安装有点防御或者面防御系统，作为防空保护的手段。随着现代反导武器系统作战性能的不断改善，使得传统反舰导弹的突防能力明显降低。

末端机动是提高反舰导弹突防效能的一个有效手段。蛇行机动已成为现役反舰导弹如俄罗斯的“白蛉”主要的末端机动方式，其目的是对付敌方舰空导弹和“密集阵”火炮等反导武器的拦截，提高突防能力。如何提高反舰导弹的末端机动能力是摆在我们面前的重要课题。

Paul Zarchan[1]研究了蛇行机动引起的拦截导弹的稳态脱靶量；Ohlmeyer[2]研究了目标作蛇行机动时拦截导弹稳态脱靶量的均方根；姜玉宪和崔静研究了蛇行机动引起的拦截导弹脱靶量的稳态分量和暂态分量，指出了蛇行机动突防策略的有效性[3]。本文在上述文献研究的基础上，重点研究了蛇行机动参数对拦截导弹脱靶量的影响。

1 反舰导弹末端蛇行机动突防的过载指令

末端机动的实现方式与导弹的控制系统密切相关。姿态控制下的末端机动可以通过姿态角指令、质心指令来实现；过载控制系统下的末端机动可通过过载指令来实现。导弹的机动性是指导弹改变飞行速度大小和方向的能力，是评价导弹飞行性能的重要指标之一。由于过载标志了机动性的大小，因而过载指令控制实现的末端机动就具有特殊意义。

过载指令是在过载控制系统中的指令输入端附加一个机动项[4]：

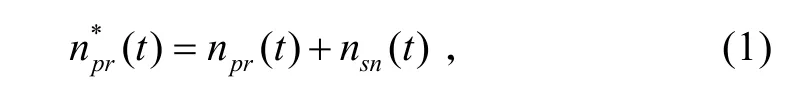
式中：npr(t)为未加入机动指令信号时的过载指令信号；为加入过载指令输入端的综合指令信号；nsn(t)为产生蛇行机动所需过载指令信号[5]。

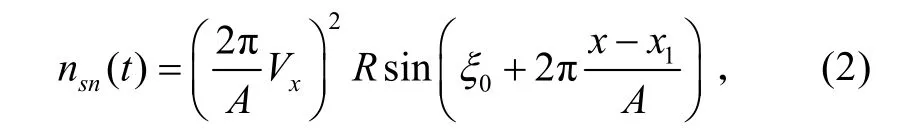
式中：A为节距，即在末端机动的一个周期内反舰导弹沿地面坐标系Ox轴方向飞行的距离；Vx为反舰导弹沿地面坐标系Ox轴方向的飞行速度分量；R为机动半径；ξ0为初始相位角；x (x1≤x≤x2)是距离控制变量，即反舰导弹的末端机动是根据飞行的距离x 进行控制，x1是末端机动的开始距离，x2是末端机动的结束距离。

为了研究问题的简化，我们假设反舰导弹沿地面坐标系Ox轴方向的飞行速度分量为常数，即Vx≡ C，则式(2)可以表示成如下的标准形式：

根据突防作战的目的，突防导弹经过一段时间机动飞行后，机动突防引起的弹道累计偏差必须为0，该约束条件数学形式为[6]：

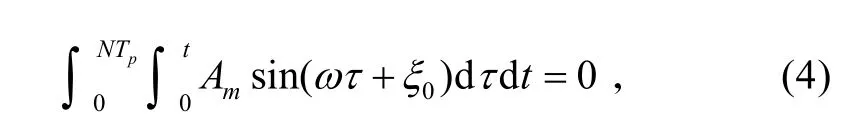
2 突防—拦截问题模型

突防—拦截问题的模型如图1所示。图1中，nL为突防导弹的机动过载；Vc为接近速度；tgo=tF−t为剩余时间，其中：tF为终端时刻，t为当前时刻；λ、λ˙分别为视线角、视线角速率；N '为有效导航比；nc、nM分别为拦截导弹的指令过载和实际机动过载；传递函数表示飞行控制系统的动力学特性，其中T是时间常数；y为拦截导弹和突防导弹在初始视线垂直方向的位置偏差，y (tf)为终端脱靶量。

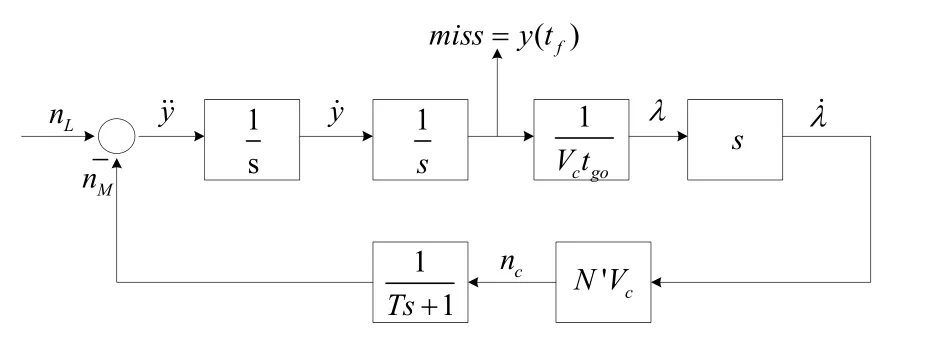
图1 突防—拦截问题模型

经以上分析，只要通过该模型求出 y (t)在终端时刻的值即 y (tf)，就得到了突防导弹的机动过载引起的脱靶量。显然，该问题属于 y (t)的终值控制问题，适合于伴随技术进行分析和求解。

根据伴随系统的转换规则[7-8]，将图1转化为图2所示的伴随系统。

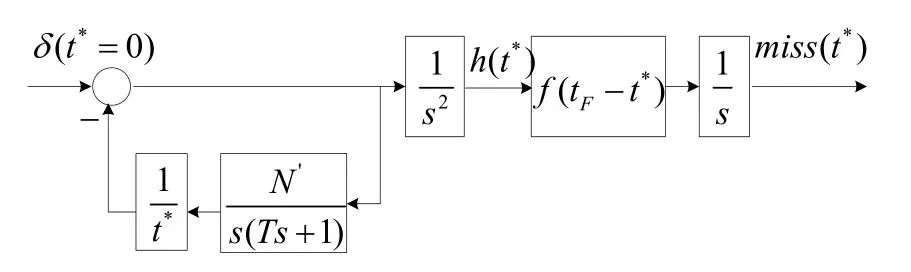
图2 突防—拦截问题伴随模型

图2中，t*为伴随系统时间变量；δ (t*)为脉冲输入；h (t*)是伴随系统的脉冲响应；h (t*)与f (tF− t*)在时域上乘积的卷积是突防导弹在时刻t=tF− t*开始蛇行机动，持续 t*后在 tF引起的脱靶量，即相应地，复域有以下关系成立：

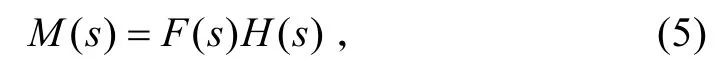
式中：M (s)、F (s)、H (s)分别是miss (t*)、f (tF− t*)，h(t*)的拉氏变换。然后对 M (s)取反拉氏变换可得到脱靶量的时域解析解。

3 仿真分析

3.1 拦截导弹的脱靶量曲线

取拦截导弹制导系统参数 N '=3、T=1s，当突防导弹作 Am=10g、ω=1.5rad/s的蛇行机动时，引起的拦截导弹脱靶量曲线如图3所示。为了对比蛇行机动的效果，图3给出了突防导弹作幅值为10 g的阶跃机动引起的拦截导弹脱靶量曲线。注意这里的横轴代表的是伴随系统时间，可以理解为突防导弹开始机动到拦截时的时间。从图3可以看出，在接近拦截前2 s时，10 g的阶跃机动可以产生接近27 m的脱靶量，如果在离拦截很长的时间开始机动，将导致脱靶量几乎为0；而突防导弹作蛇行机动突防时，拦截导弹脱靶量经过一短暂时间后呈频率为1.5 rad/s的正弦规律变化，增加了拦截的不确定性，从而增加了突防导弹的突防概率。

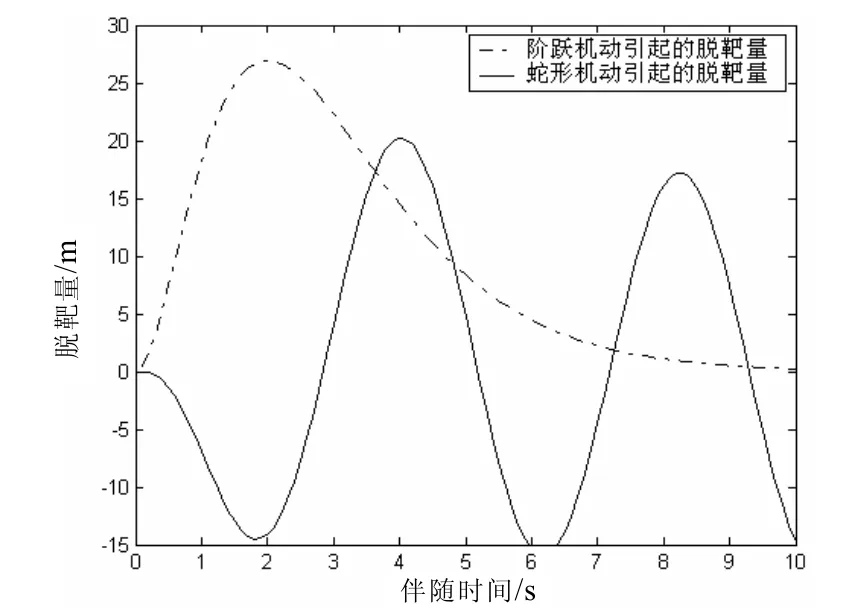
图3 拦截导弹脱靶量曲线

3.2 蛇行机动参数对拦截导弹脱靶量的影响

对突防导弹来说，关心的是正弦规律变化的峰值稳态脱靶量。影响反舰导弹突防的因素包括蛇行机动过载幅值mA、蛇行机动频率ω、拦截导弹控制系统时间常数T 以及有效导航比 N'。由于拦截导弹的参数是我们无法控制的，当假设其在一定的条件下，分析蛇行机动参数对峰值脱靶量的影响。

3.2.1 机动频率对峰值脱靶量的影响

为便于分析，令 Tω为归一化的机动频率，峰值脱靶量2/mA T为归一化的峰值脱靶量，则归一化的机动频率与归一化的峰值稳态脱靶量之间的关系如图4所示。

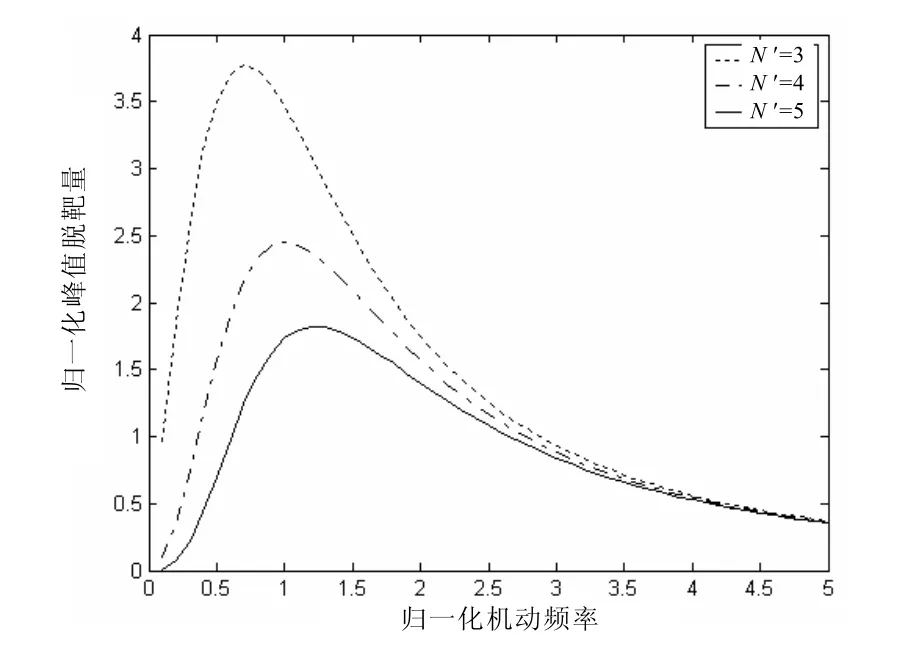
图4 归一化机动频率与归一化峰值脱靶量之间的关系

从图 4可以看出，在 N '一定的条件下，突防导弹的机动频率不是越大越好，也不是越小越好，而是存在一个最优的归一化机动频率，使拦截导弹的归一化脱靶量达到最大值。不同的N '值对应不同的归一化机动频率，N '=3时对应的最大机动频率ωT=0.7；N '=4时对应的最大机动频率ωT=1；N '=5时对应的最大机动频率 ωT=1.2。

3.2.2 机动过载幅值对峰值脱靶量的影响

拦截导弹制导系统参数同3.1节叙述，机动过载幅值与峰值脱靶量之间的关系如图5所示。

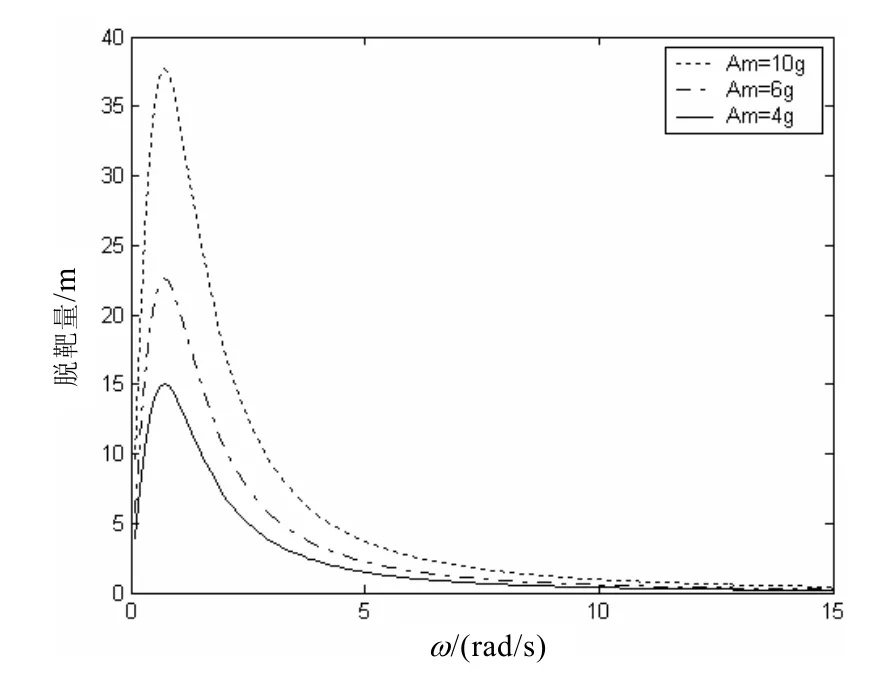
图5 机动过载幅值与峰值脱靶量之间的关系

从图5可以看出，峰值脱靶量随机动幅值的增大而增大。这里的机动幅值代表突防导弹的法向加速度，当速度相同时，法向加速度越大，导弹改变方向的能力就越强，导弹越能作弯曲度大的飞行，即导弹的法向机动性就越好。在不超过导弹允许的最大法向过载的情况下，采用尽可能大的法向加速度，即机动过载幅值尽可能大。根据式(3)得知，突防导弹的过载幅值与机动频率和机动半径有关，这也就是说在满足突防导弹性能的条件下，要求机动频率的平方与机动半径的乘积取最大值。

我们假设突防导弹的Vx=2Ma，末端15 km处开始机动，在5 km处停止机动；在拦截导弹制导系统参数N=3，T=0.5时，由3.2.1节可知最优的机动频率为ω=1.4rad/s，对应的机动周期为4.5 s，从而得到机动的周期数为3；若突防反舰导弹这时以最大机动过载幅值作蛇行机动，由3.2.2节可以得到蛇行机动的最优机动半径为50 m。

4 结束语

本文对反舰导弹末端机动突防的效果进行了仿真研究，结果表明，在一定的条件下，反舰导弹突防存在一个最优的机动频率和最优的机动半径，这为反舰导弹研制和作战使用提供了理论上的参考。由于蛇行机动是非平面机动的基础，所以文中的方法和结论也可以推广到非平面机动的效果分析。

[1]ZARCHAN P.Proportional navigation and weaving targets[J].Journal of Gudiance and Dynamics,1995,18(3):969-974.

[2]OHLMEYER E J.Root-mean-square miss distance of proportional navigation missile against sinusoidal target[J].Journal of Gudiance and Dynamics,1996,19(3):563-568.

[3]姜玉宪,崔静.导弹摆动式突防策略的有效性[J].北京航空航天大学学报,2002,28(2):133-136.

[4]李聪颖,王凤莲,顾文锦,等.侧滑转弯反舰导弹末端机动的控制研究[J].战术导弹控制技术,2005,49(2):2-6.

[5]顾文锦,赵红超,王凤莲.反舰导弹末端蛇行机动的控制信号设计[J].航天控制,2005,23(1):58-61.

[6]谢邦荣,伊健.空射巡航导弹末端机动突防策略仿真研究[J].弹箭与制导学报,2004,24(2):145-149.

[7]ZARCHAN P.Tactical and strategic missile guidance[M].3rd ed.American Institute of Aeronautics and Astronautics,Washington DC,1997:31-50.

[8]GUFIL P,JODORKOVSKY M.Neoclassical guidance for homing missiles[J].Journal of Guidance,Control,and Dynamics,2001,24(3):452-459.