随机需求条件下三级供应链数量折扣协调策略
2010-03-23汪传旭
汪传旭
(上海海事大学 经济管理学院,上海 200135)
近年来,供应链协调问题日益受到学术界和企业界的关注.供应链企业认识到,通过供应链协调与合作而实现的有效管理将对供应链各方带来利益.在供应链中,如果各方彼此合作,对订单量进行优化,可以实现供应链整体成本的下降.目前,国内外学者在供应链协调方面开展了大量研究,并提出供应链实现协调的有效策略,这些协调策略主要体现为:回购策略[1-6]、数量折扣策略[7-10]、供应商管理库存策略[11-12]、数量灵活性策略[13-15]和其他策略[16-19].上述文献在设计供应链协调策略时主要考虑由制造商(或供应商)和零售商(或购买商)组成的两级供应链.近年来,也有少数学者考虑三级供应链的协调问题[20-22].
本文考虑由供应商、制造商和零售商组成的三级供应链,供应链需求具有随机性.本文假设三级供应链的核心主导成员是制造商,其在供应链协调中起关键作用,能从数量折扣策略中获取潜在的成本下降所带来的所有或者大部分利益.本文与现有的关于三级供应链协调的研究文献相比,主要呈现如下特点:1)主要考虑数量折扣策略;2)在分析三级供应链协调时,不仅研究供应链成员的订单量决策,而且同时研究供应链成员的库存决策.
1 模型参数与假设条件
本文模型参数设置如下:s、m、r分别代表供应商、制造商和零售商的下标;D为零售商(制造商和供应商)单位时间内产品的平均需求量;ρi为成员 i能力利用率(单位时间需求量/单位时间生产量), i={s,m},ρi<1;Ci为成员i每批订单的生产启动或订单成本,i={s,m,r};hi为成员i单位时间内单位产品所发生的持有成本,i={s,m,r};hμ为制造商原材料单位时间内单位产品所发生的持有成本; TCi为采用折扣策略之前成员i的最优成本,i={s, m,r};TCsc采用折扣策略之前供应链最优总成本, TCsc=TCs+TCm+TCr;Q为零售商订单量;nm代表制造商订单量是零售商订单量的整数倍数;ns代表供应商订单量是制造商订单量nmQ的整数倍数;ri为成员i再订货点水平,i={m,r};Si为成员i安全库存量,i={m,r};ei为成员i单位时间内单位产品的缺货成本,i={m,r};Li为成员i面临的进货提前期,i={m,r};Dm(nmQ)为供应商对制造商的订单量nmQ所提供的单位产品折扣;dr(Q)制造业对零售商的订单量Q所提供的单位产品折扣.
本文假设三级供应链是由一家供应商、制造商和零售商所组成的简单供应链,目前的相关文献都采用类似的假设[20-22].此外,考虑零售商和制造商采用连续库存补充策略.零售商向制造商发出的订购量为Q,并产生订单成本Cr.制造商按能力利用率ρm的进度生产产品并产生启动成本 Cm.当零售商手中库存量下降到再订货点 rr时即向制造商发出订货.制造商库存情况见图 1[23].
假设零售商进货提前期内需求服从正态分布,其概率密度函数为

制造商向供应商发出的订购量为 nmQ,并产生订单成本Cm.供应商按能力利用率 ρs的进度生产产品并产生启动成本Cs.当制造商手中库存量下降到再订货点rm时即向供应商发出订货.供应商库存情况见图2.
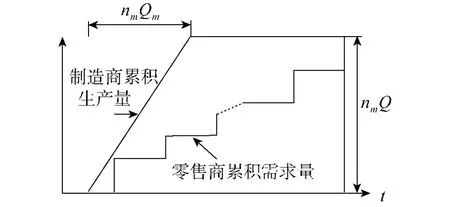
图1 制造商库存情况Fig.1 Inventory formanu facturer
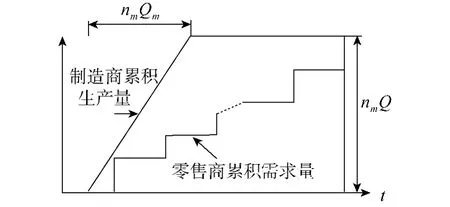
图2 供应商库存情况Fig.2 Inventory for supplier
2 未提供数量折扣时的模型构建
在未提供数量折扣时,零售商、制造商和供应商各自追求成本最小化,并对各自的订单量和库存水平进行决策.
2.1 零售商决策模型
对于零售商而言,制造商没有提供数量折扣时,其单位时间内期望成本为
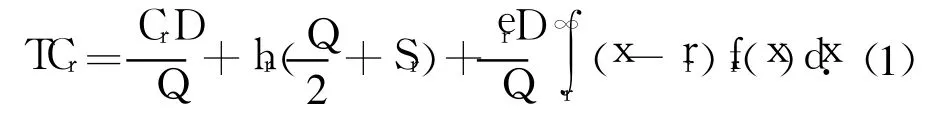
由于进货提前期内需求服从如假设条件所示的正态分布,有

其中,
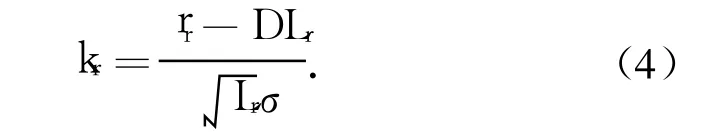
式中:φ(kr)为右损失函数,φ(t)为标准正态分布密度函数.
因此,式(1)可以改写为

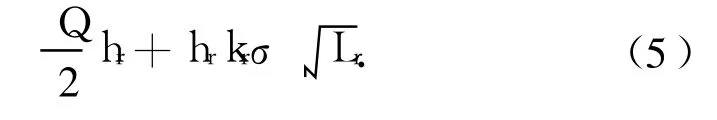
对Q、kr分别求导,并令其等于零,于是得到
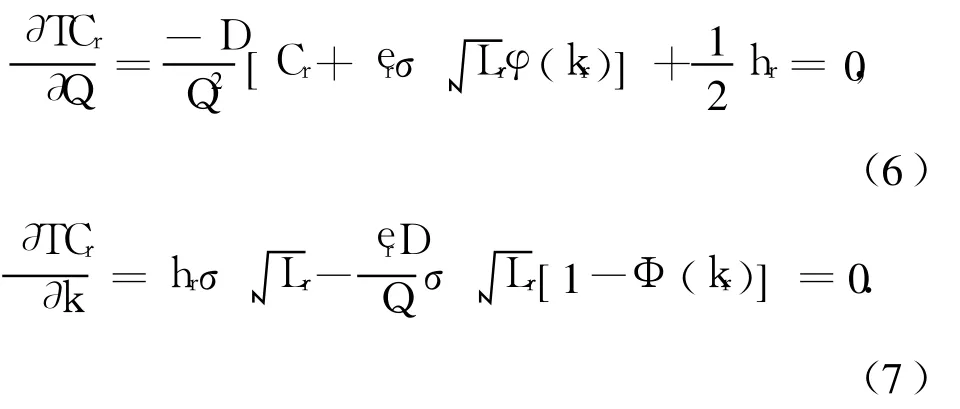
式中:φ(kr)可以表示为φ(kr)=φ(kr)-kr[1-Φ(kr)],φ(kr)、Φ(kr)分别为标准正态密度函数和分布函数.
根据式(6)、(7),分别得到
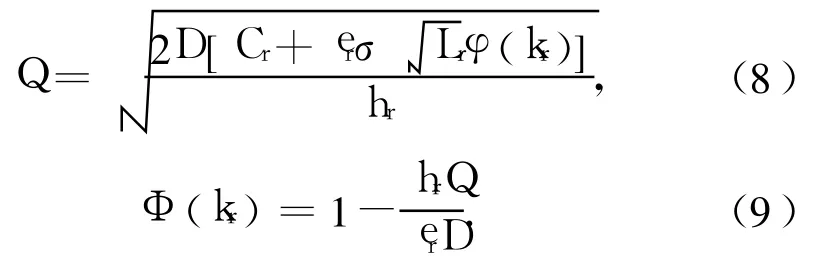
根据式(6)和式(7)分别对Q、kr求导可以看出,总成本函数为Q和kr的凸函数.根据式(8)和式(9)可以利用迭代算法求出使零售商成本达到最小时的Q和kr的值,以及零售商最小总成本TC0r.
2.2 制造商决策模型
对于制造商而言,供应商没有提供数量折扣时,其单位时间内期望成本为

同理,由于制造商进货提前期内需求服从如假设条件所示的正态分布,因此

因此,式(10)可以改写为
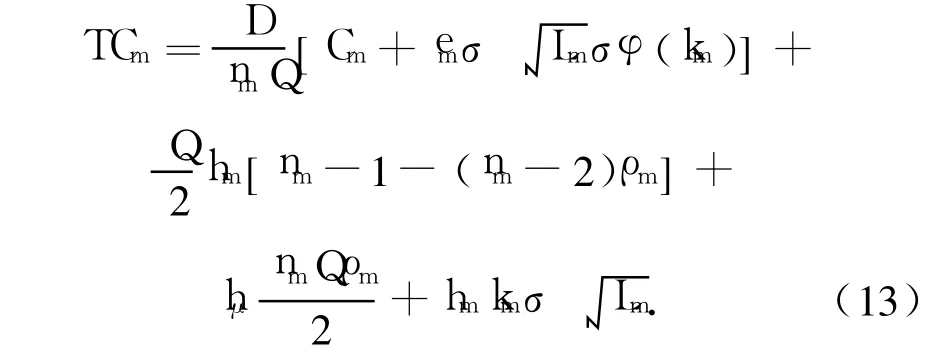
对于式(13),在km给定条件下,要使TCm取最小值,nm必须满足:TCm(nm)≤TCm(nm+1)和TCm(nm)≤TCm(nm-1),于是得到

因此,使TCm达到最小值时的nm必须满足:
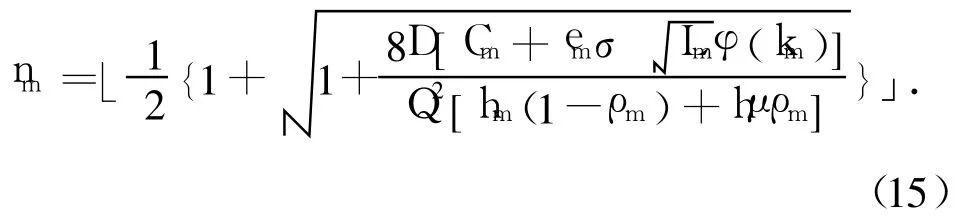
对于式(13),在nm给定条件下,对km求导,并令其等于零,得到
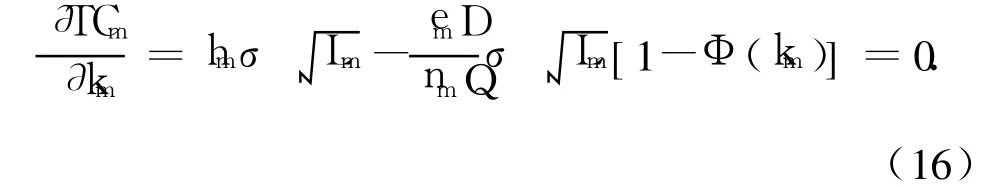
显然,在nm给定条件下,TCm是km的凸函数,于是可以得到

根据式(15)和式(17),利用迭代算法可以求出使制造商成本达到最小时的 nm和 km的值,以及制造商最小总成本TC0m.
2.3 供应商决策模型
对于供应商而言,其单位时间内期望成本为

对于式(18),要使TCs取最小值,ns必须满足TCs(ns)≤TCs(ns+1)和TCs(ns)≤TCs(ns-1),于是得到
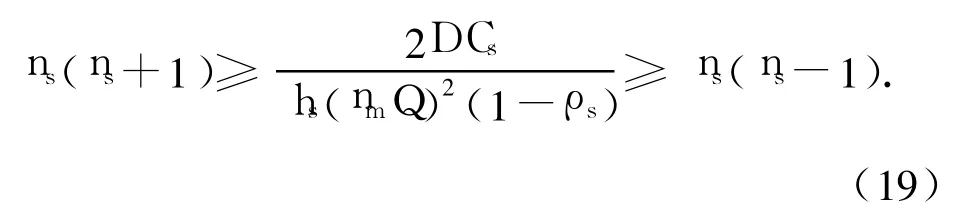
因此,使TCs达到最小值时的ns必须满足:
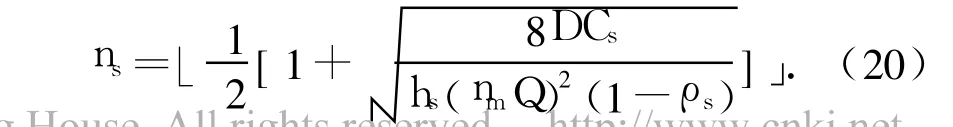
利用式(20)可以得到供应商成本最小时的ns值和供应商最小成本TC0s.
由式(20)可以看出,随着制造商订单量nmQ的上升,供应商成本最小时的ns值下降,从而引起供应商最小成本的变化.为此,引入定理 1.
定理1 供应商最小成本是依赖于 ns的凸函数,当 0≤ρs<1/2,ρs=1/2,或者 1/2<ρs≤1时,供应商最小成本随着nmQ的上升分别呈现下降、不变和上升趋势.
证明 对于给定的ns,TCs是nmQ的凸函数.当TCs最小时,最小成本由于
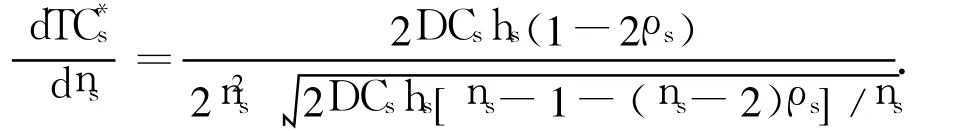
因此,当0≤ρs<1/2,ρs=1/2,或者 1/2<ρs≤1时,随着ns的上升分别呈现上升、不变和下降趋势.由于ns是nmQ的递减函数,因此,当0≤ρs<1/2s=1/2,或者 1/2<ρs≤1时,供应商最小成本随着nmQ的上升分别呈现下降、不变和上升趋势.
从定理 1可以看出,一般情况下,随着供应商能力利用率 ρs下降,供应商期望收到较大的订单批量nmQ,实现总成本下降.如果供应商能够控制其收到的订单批量,则供应商能够降低总成本.
3 提供数量折扣时的模型构建
在存在数量折扣时,对于零售商来说,制造商提供给零售商的数量折扣所引起的零售商单位时间总成本必须等于未提供数量折扣时零售商的单位时间最低成本.因此
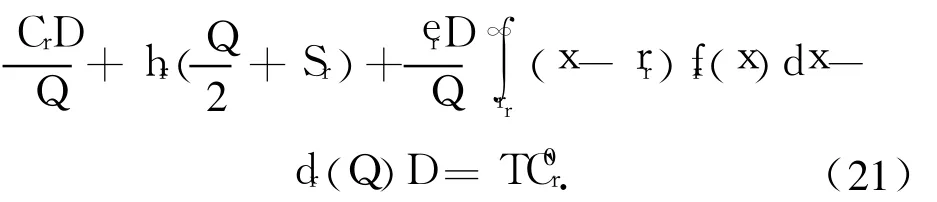
对于制造商来说,制造商向供应商发出的订单量nmQ会引起供应商成本的改变.根据定理1可知,随着nmQ的上升,供应商总成本可能呈现递增,也可能呈现递减.如果供应商总成本随着nmQ的上升而下降,则制造商nmQ利用其讨价还价能力要求供应商从其成本节省中提供数量折扣;如果制造商的订单量引起供应商总成本上升,则制造商不要求供应商提供数量折扣.因此,在 nmQ一定条件下,供应商单位货物折扣可以表示为
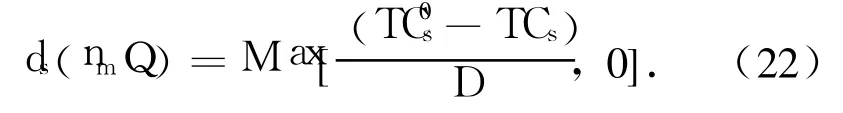
利用上述结果,可以得到制造商单位时间的成本函数为
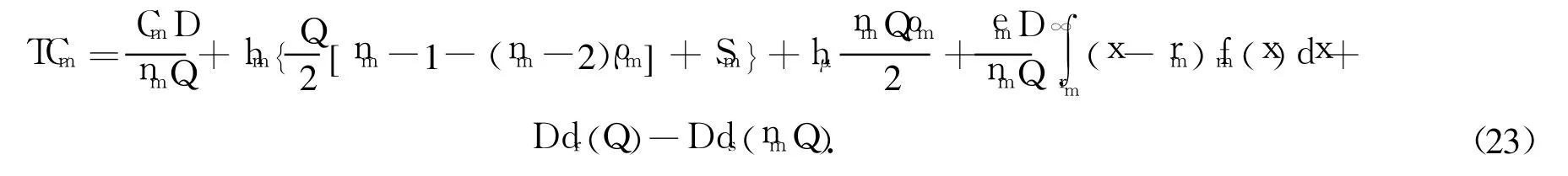
将式(21)、(22)代入到式(23),得到

根据式(2)、(3)、(11)和(12),得到

根据式(22),当ds(nmQ)时,此时式(24)等价于由制造商和零售商组成的两阶供应链决策问题.
由于式(25)所表示的TCm为Q的凸函数,在 ns和nm给定条件下,由∂TCm/∂Q=0得到使制造商成本最小的订单量为

由于式(25)所表示的TCm为km和kr的联合凸函数,因此,在 Q、ns和 nm给定条件下,可以由∂TCm/∂km=0,∂TCm/∂kr=0得到km和kr的值,即


将式(26)代入到式(24),得到

式中:

对于式(29),若ns给定,则TCm的最小值可以通过最小化得到.令消除其中与nm无关的常数项,不难得到

显然,如果(1-2ρm)hm≥hr,则F(nm)是nm的增函数,此时,当nm=1时,F(nm)取最小值.否则,可以通过如下2个不等式确定使F(nm)达到最小值时的

于是得到

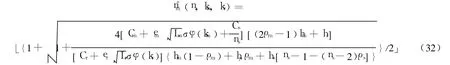
为了对上述模型进行求解,设计如下算法:
1)令ns=1,执行①~⑤.
①令km=kr=0,得到φ(km)=φ(kr)=0.398 9;
②利用式(32)计算nm;
③利用式(26)计算Q;
④利用式(27)和式(28)计算km和kr;
⑤重复步骤②~④,直到km、kr和 Q的值没有变化为止.
2)根据步骤1)的(ns,nm,km,kr,Q),计算相应的TCm值;
3)根据式(20)修改 ns,重复步骤1)和步骤2);直到根据连续2次ns所得到的TCm值没有变化为止;若根据最后一次ns所得到的TCm为则为最优解.制造商和零售商的最优订货点分别为和
4 算例分析
4.1 基本数据
为了验证上述模型,考虑如下算例:周需求量服从均值为D=5 000,标准差 σ=50的正态分布,供应商、制造商和零售商的生产启动或订单成本分别为Cs=$20、Cm=$30和Cr=$60,供应商、制造商和零售商的单位库存持有成本分别为hs=$1.2, hm=$3.6和hr=$7.2,制造商原材料单位库存持有成本为hμ=$1.5,制造商和零售商的单位缺货成本分别为em=$20和er=$40,供应商和制造商的能力利用率分别为ρs=ρ=0.6,制造商和零售商所面临的订货提前期分别为Lm=3周和Lr=5周.
4.2 未提供数量折扣情形的模型计算结果
对未提供数量折扣情形的模型进行计算,结果为:Q=655,kr=1.985,km=1.673,rr=25 222,nm=三级供应链总成本
4.3 提供数量折扣情形的模型计算结果
对提供数量折扣情形的模型进行计算,还可以进一步考虑如下情形:
1)制造商仅要求供应商提供数量折扣
其计算结果为:q=106,kr=1.985,km=1.963,三级供应链总成本
2)制造商仅向零售商提供数量折扣
3)制造商不仅要求供应商提供数量折扣,而且向零售商提供数量折扣
其计算结果为:Q=506,kr=2.092,km=1.806, rr=25 233 919,nm=1,rm=15 156.404,ns=1,三级供应链总成本
由上述结果可以看出,通过采用数量折扣协调策略以后,三级供应链总成本明显下降.由于制造商在三级供应链协调中起主导作用,因此,通过三级供应链协调而引起的总成本下降全部由制造商独享,因此,制造商总成本比协调前下降了 488.009,而供应商和零售商仍然可以维持协调以前的最低成本.如果仅考虑二级供应链协调,制造商要么仅要求供应商提供数量折扣,要么仅向零售商提供数量折扣,这两种情形下所引起的三级供应链总成本都高于三级供应链协调时(即制造商要求供应商提供数量折扣,同时向零售商提供数量折扣)的总成本,但低于未提供数量折扣时三级供应链总成本.
5 结束语
本文建立由供应商、制造商和购买商所组成的三级供应链的数量折扣协调模型,并设计相应的模型求解算法.最后运用算例进行分析,结果表明,采用数量折扣策略协调三级供应链,三级供应链总成本明显下降.如果仅考虑二级供应链协调,制造商要么仅要求供应商提供数量折扣,要么仅向零售商提供数量折扣,这两种情形下三级供应链总成本都高于三级供应链协调时(即制造商要求供应商提供数量折扣,同时向零售商提供数量折扣)的总成本,但低于未提供数量折扣时的三级供应链总成本.本文研究结果能给企业决策提供参考依据,同时论文中的研究结果还有待进一步完善.现实中的三级供应链节点企业可能是多个企业,这可以作为将来进一步研究的一个方向.另一个研究方向是考虑制造商和零售商采用其他库存补充策略的情况下,三级供应链协调的数量折扣决策问题.
[1]EMMONSH,GILBERTSM.The roleof returns policies in pricing and inventory decisions for catalogue goods[J]. Management Science,1998,44(2):276-283.
[2]KANDLE E.The right to return[J].Journalof Law and E-conomics,1996,39(1):329-356.
[3]PASTERNACK B A.Optimal p ricingand returns policies for perishable commodities[J].Marketing Science,1985,4 (2):166-176.
[4]贾 涛,徐 渝,陈金亮.回购策略:存货促销与供应链协调[J].预测,2006,25(1):76-80.
JIA Tao,XU Yu,CHEN Jinliang.Buy back policies:retailer promotionswith inventories and supply chain coordination[J].Forecasting,2006,25(1):76-80.
[5]陈旭.考虑广告影响的随机需求环境下的供应链退货策略[J].系统工程理论方法应用,2005,14(4):313-317.
CHEN Xu.Supp ly chain coordination under return policy with advertising dependent demand[J].Systems Engineering-Theory Methodology Application,2005,14(4):313-317.
[6]肖振伟,李 华.基于退货策略的供应链合作研究[J].工业工程与管理,2005(5):52-60.
XIAO Zhenwei,LIHua.Study of supply chain cooperation based on returns policies[J].Industrial Engineering and Management,2005(5):52-60.
[7]LEEH L,ROSENBLATT M J.A generalized quantity discount p ricingmodel to increase supplier's profits[J].Management Science,1986,32:1177-1185.
[8]MONAHAN JP.A quantitative discount pricingmodel to increase vendor profits[J].Management Science,1984, 30:720-726.
[9]刘剑虹,邓益华.二次博弈下供应链的均衡订货批量研究[J].中国管理科学,2004,12(6),42-45.
LIU Jianhong,DENG Yihua.Thequantity discount policy of supp ly chain under quadratic game[J].Chinese Journal of Management Science,2004,12(6):42-45.
[10]单汩源,邓益华.二次博弈下的供应链数量折扣策略[J].中国机械工程,2003,14(18):1603-1607.
SHAN Guyuan,DENGY Yihua.Quantity discount policy of supp ly chain underquadratic game[J].China Mechanical Engineering,2003,14(18)1603-1607.
[11]唐桂风,郑称德.基于采购协议价格的 VMI协调机制研究[J].科技进步与对策,2005(12):5-7.
TANG Guifeng,ZHENG Chengde.VMI coordination mechanism based on purchasing agreement price[J].Science Technology Progress&Strategies,2005(12):5-7.
[12]赵 晶,史保东,供应商管理库存与供应链协调机制[J].辽宁经济,2005(11):93.
ZHAO Jing,SHI Baodong.Vendor-managed inventory and supply chain coordination mechanism[J].Liaoning Economics,2005(11):93.
[13]MILNER JM,ROSENBLATT M J.Flexib le supply contracts for short life-cycle goods:the buyer's perspective [J].Naval Research Logistics,2002,49:25-45.
[14]TSAY A A.The quantity flexibility contract and suppliercustomer incentives[J].Management Science,1999,45: 1339-1358.
[15]TSAY A A,LOVEJOYW S.Quantity flexibility contracts and supply chain performance[J].Manufacturing and Service OperationsManagement,1999,1:89-111.
[16]DONOHUEK L.Efficientsupply contract for fashion goods with forecastupdating and two productionmodes[J].Management Science,2000,46:1397-1411.
[17]LEE H L,WHANG S.Decentralized multi-echelon supp ly chains:incentives and information[J].Management Science,1999,45:633-640.
[18]LISX,HUANG Z,ZHU J,CHAU P Y K.Cooperative advertising,game theory and manufacturer-retailer supp ly chains[J].Omega,2002,30:347-357.
[19]QI X,BARD J F,YU G.Supply chain coordination with demand disruptions[J].Omega,2004,32:301-312.
[20]MUNSON C,ROSENBLATTM J.Coordinating a three level supply chain with quantity discounts[J].IIE Transactions,2001,33::371-384.
[21]DING D,CHEN J.Coordinating a three level supp ly chain with flexible return policies[J].Omega,2008,36(5): 865-876.
[22]易雪辉,唐小我.需求价格相关的非中心化三级供应链的协调研究[EB/OL].[2005-08-16],www.paper. edu.cn.
[23]DAYA M B,HARIGA M.Integrated single vendor single buyermodelwith stochastic demand and variab le lead time [J].International Journal of Production Economics, 2004,92(1):75-80.
[24]JOGLEKAR PN.Comments on"A quantity discount pricingmodel to increase vendor profits"[J].Management Science,1988,34(11):1391-1398.
