基于遗传算法的旋律匹配模型研究

秦 静,王醒策,周明全,刘新宇

(1.北京师范大学 信息科学与技术学院,北京 100875;2.大连大学 信息工程学院,辽宁大连 116622;3.中科院计算技术研究所,北京 100080)

近年随着Internet的发展,音频数据呈指数倍增长.传统基于文字标注的检索已经不能满足海量多媒体数据检索需要,因此基于内容的音乐信息检索(MIR,music information retrieval)很快成为信号处理、模式识别和数据挖掘等领域研究者致力研究的热点之一.从 20世纪 90年代中期开始,国内外对基于内容的音乐信息检索进行了多方面的研究.英国南安普顿大学Asif Ghias在1995年首先发表MIR论文[1],同时发布QBH(query by humming)哼唱检索系统,开创了此研究的先河.此后,Lie Lu[2]等在音高的基础上增加了音高差、音符长度,构成旋律表示单位.Jyh-Shing Roger Jang等提出HFM实现旋律匹配.国内近年来开始对该问题进行逐步深入的研究.上海交通大学李扬[4]提出线性对齐匹配算法(linear alignmentmatching),浙江大学冯雅中等[5]应用递归神经网络进行音频匹配.虽然已经在音乐特征选择、表示和匹配取得一定成果,但由于音乐信号的不稳定性及其感知分析的复杂性使得大规模MIR系统及其应用发展缓慢.目前制约基于内容音乐检索技术发展的关键问题表现为 3个方面:如何提取音频特征实现音乐内容表征;如何描述音乐特征及用何种方法进行特征匹配.本研究在已有研究基础上,通过基音提取和动态阈值分割音符算法实现了音乐特征的提取,通过遗传算法和动态时间扭曲函数实现特征匹配,提高了算法的速度及精度,为后续相关研究提供了技术支持.

1 旋律的表示模型及其匹配技术框架

音乐特征大致可分 3个级别——物理特征,声学特征和感知特征,如图 1所示.物理特征主要是指按照一定格式通过物理载体记录的音频内容,表现为流媒体形式.声学特征主要包括时、频域特征,如基音频率、短时能量、过零率、LPC系数和MFCC系数等,它们是音频本身的表现特征,常被用于语音识别的各个阶段.而感知特征则体现了人对音乐感受的描述,如音高、节奏、音强、音色等.感知特征通常可在物理特征基础上提取出来.与物理特征相比较,它更能体现人类识别特点并帮助人类判断音乐内容.

音乐是随时间变化的离散音符序列,然而感觉上却是音符随时间变化的完整实体.格式塔理论(Gestalt theory,GT)是一个关于心理现象、心理过程以及心理研究的应用理论架构.此理论证明人类感知形式下潜藏着一种相近、相似、连续等规律的法则,能够揭示在给定刺激特征的情况下,哪种模式的组织形式将会被感知到,因此可以用来说明音符被感知的方式.1986年Dow ling[6]证明旋律满足格式塔理论,即具有相近性、相似性和连续性.所以文中,将音乐主要感知特性——旋律作为表征音乐的特征.音乐的旋律轮廓即为音高随时间的变化特性,而音高又是由音乐的基音频率来决定的,因此通过提取音高并用合适的模型描述音高就可以提取和描述旋律轮廓.

在前期的工作中 提出了基于标准模板和哼唱输入模板的旋律表示模型,并从用户哼唱的音频文件中提取了输入音高模板,再根据音乐文件的简谱与基音频率的关系建立了标准音高模板,对于这 2个同属于基音频率范畴的模板具备可比性,并且在归一化后具有相似的外形.本文的工作就是在上述研究基础上,对旋律的表示模型进一步完善和改进,并提出合适的匹配算法进行匹配得到最终的检索结果.

图1 音乐的特征级别表示Fig.1 The p resentation ofmusic character level

2 基于遗传算法的旋律轮廓对齐算法

MIR系统框架流程如图 2所示.人的声音频率范围在50～3 200 Hz,而音乐上使用的音高通常在16～7 000 Hz(相当于音符C2～A 5),两者存在一定差异[8].人哼唱的基频往往低于标准基频若干倍,并且由于每个使用者音域并不相同,同样会造成基音变异[9].如果对输入模板和标准模板简单归一化,则由于忽略了音高轮廓的细节信息,而导致检索结果失真[10-11].

因此,考虑用标准音高模板频率范围内的模板去逼近原哼唱模板的轮廓,并代替原哼唱模板进行匹配.此算法将输入音高模板线性平移,在使其与标准音高模板在音高范围上接近的基础上,保留原有轮廓细节信息,从而降低了直接归一化造成的轮廓信息丢失所带来的误差.遗传算法作为一种优化算法在全局并行性和全局寻优能力上具有突出特点.此算法在不需要问题先验知识的条件下,同样可求得问题最优解.因此考虑应用遗传算法在现在标准音高频率范围内搜索与输入模板最相似的模板,从而达到模板平移的目标.

旋律对齐问题可以描述如下:输入模板为P= {p1,p2,…,pi,…,pn},其中pi为某一音符,n为音符个数.将此模板缩放到音符的标准音高模板频率范围中,得到逼近模板Q={q1,q2,…,qi,…,qn},2模板相似程度可以通过模板向量夹角的余弦值来度量.算法目的是找到与P模板夹角余弦值最大的Q模板.

图2 MRI系统框架流程图Fig.2 The framework of the MIR system

2.1 染色体编码

将钢琴音符基频作为标准音高模板,然后把乐谱转化为钢琴音高模板.根据对模板对齐问题的描述,采用可变长十进制染色体编码,每一个染色体表示一种逼近方案得到的模板,染色体的长度可随模板长度的变化而变化.在标准音高模板中,通常简谱中所用到的音符分布在 3个八度,即从低音“do”到高音“Si”,总共是 21个音符,音符与标准基频对应关系如表1所示.

表 1 音符与标准基频对应关系Table 1 The relationship between the scaleand frequency

染色体中的每个基因位取表 1中的一个数字,这样长度为n的输入模板,可用长度为n的染色体来逼近,得到整个染色体十进制串可以表示标准基频序列,不断逼近输入模板得到的标准模板.对某一输入模板P={p1,p2,…,pi,…,pn},染色体编码的结构如表 2所示,gi表示一个基因位,i=1,…,n, gi∈{x|x为标准基音频率},gi与逼近模板Q={q1, q2,…,qn}中的qi对应.初始种群时gi随机生成,可以取 21个音符标准基频中的任意数.用得到的染色体代替Q,计算 P与Q之间的相似度,按照相似度的大小对初始种群进行排序,然后进行选择、交叉、变异操作,让相似度更高的解逐步保留下来,最终得到最优解,即与P最相似的逼近模板Q.由于编码时选择十进制编码,所以解码过程相对简单.

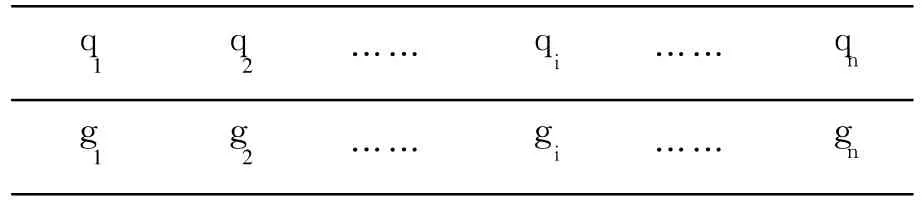
表2 染色体编码结构Table 2 The coding of the gene

2.2 适应度函数的定义

输入模板P={p1,p2,…,pi,…,pn},通过遗传操作得到逼近模板为Q={q1,q2,…,qi,…,qn}.算法目的是找到与 P模板夹角余弦值最大的 Q模板,因此适配函数可按式(2)进行选取.

根据GA算法最优的染色体应该具有最大的适应度函数,

因此可以把式(2)作为适应度函数,从而得到最佳的逼近模板.

2.3 遗传操作

初始随机生成L个染色体,选择操作将适应函数值最大的染色体直接复制到下一代种群中,这可以保存上一代最优的染色体,以免丢失可能的最优解.其他染色体采用随机遍历抽样来选择,设染色体Si的选择概率为其适应函数值占种群适应函数值总和的百分比,则染色体Si选择概率Ps(Si)定义为

F(Si)为染色体Si的适应函数值,L为种群中染色体的个数.经过选择操作后,良好的染色体将被保留,劣质染色体将被淘汰,种群中染色体整体个数不变,这样L个染色体被选定进入交配群进行交叉和变异操作.

交叉操作将在 2个染色体中进行,将 2个染色体的部分对应基因串相互交换,使染色体进化.采用双点交叉,在交配池中随机选择 2个串L1和 L2,随机选择 2个交叉位 x1、x2,对 2个位串中两位置的中间基因片段进行交换,得到 2个新的个体.交叉后的染色体会具有新的模式组合,可能会产生更高的适配值.

变异算子由于采用非二进制表示,通过扰乱基因值和并随机选择允许新值实现变异.变异后的后代染色体还要和父代染色体进行适应函数值比较,如果高于父代的适应函数值,则复制到新一代中,否则,将父代染色体直接复制到新一代中.

2.4 算法描述

将输入模板P的十进制序列作为输入,通过遗传算法即得到对齐后的逼近模板,基于遗传算法的旋律模板对齐算法详细描述如下:

1)初始化染色体种群 B,随机产生 L个染色体组成种群,S为种群中的染色体.设F(S)= cos(P,S),F(S)为适应度函数.令i表示当前的遗传代数,MAXGEN表示最大染色体的遗传代数, i=0.

2)计算当前种群 B中的每一个染色体的适应函数值.

3)按照选择、交叉、变异概率,应用复制、交叉、变异算子进行遗传运算,生成新一代种群B1,令i= i+1.

4)判断,是否i＜MAXGEN,是则转向2),否则算法结束,输出适应函数值最大的染色体S.

3 加权综合旋律模板匹配算法

欧几里德距离是时间序列相似性研究中应用最广泛的相似度度量.对于输入音高模板 P和标准音高模板S的欧式距离计算公式如下:

欧式距离计算简单,容易理解,在交变换下保持不变,满足距离三角不等式,支持多维空间索引.但是此算法要求向量基准线必须保持一致,所以若 2向量波形基本相似,但波峰和波谷位置略有偏差时,用欧式距离度量也不会认为两者相似.

DTW距离能够支持序列在时间轴上的伸缩,使得相似波形能够在时间轴上对齐匹配.与欧式距离不同,DTW距离不要求模板之间点与点进行一一对应的匹配,允许点自我复制后再进行对齐匹配.这使得当模板在时间轴上发生弯曲时,仍然可以在弯曲部分进行自我复制,使 2个模板之间的相似波形可以对齐匹配.

使用一种基于累积距离矩阵的动态规划方法计算2个模板之间的DTW距离.对于输入音高模板P和标准音高模板S其累积距离矩阵为

由于DTW不断的计算2个向量模板的距离寻找最优匹配路径,这样就保证了它们之间最大的轮廓相似性.但是DTW算法在整句音符相差不多时,容易造成区分度不高的问题.因此,本文给出了加权综合的相似度匹配算法.

首先,要求用户在哼唱时至少哼唱一个整句,这样假定模板长度一定.同时,将歌曲划成整句后形成在数据库中存储的钢琴模板。通过式(6)进行匹配.

式中:Ls为整句模板音符个数;Ln为输入音频信号中包含的音符个数.

这样只考虑长度与输入音符个数相似的整句,同时只保留整首歌曲的最大相似度.并且,当遇到音符分割产生较大误差时,即使忽略整句与输入之间相差的音符,仍将导致较小的相似度.DTW算法允许相似的外形进行匹配,甚至允许片断在时间轴上有一些偏移.所以,使用DTW算法来解决音符分割带来的误差.最后,融合 2种算法,按照式(7)得到最终的相似度.

式中:Sv为欧式距离得到的相似度,SD为DTW算法得到的相似度,w1,w2为实验得到的权值, w1+w2=1.

由此得出最后的匹配相似度S,根据N-best原则,按照相似度最高的 3首歌曲名作为输出结果.

4 实验验证

4.1 算法原形系统介绍

原形系统如图 3所示,数据库中存放了 5 000首流行音乐,标准音高模板向量集包含 8 932个模板向量,每首歌曲都对应若干互不重复的标准音高模板向量.

系统开发的是一个基于实验的平台,因此省略了一些细节,仅突出了旋律表示模型建立音乐检索2大功能.系统测试界面设计如图 3.

图3 系统界面Fig.3 The interface of the system

首先用户选择打开 1个音频文件,可以求其幅度函数、幅差函数、基音频率、生成的模板和对齐后的模板,将看不到的音频数据以图表的形式表现出来,便于在实验过程中验证算法,发现规律、检查错误,以达到更佳效果.

4.2 遗传算法实验结果及其分析

实验中应用麦克风以 11.025 kHz、采样精度8 bit对输入的音乐信号采样,采用带通滤波器滤波,其上截止频率fH=3 400Hz,下截止频率范围为60～100 Hz,采用了一阶数字滤波器H(Z)=1-μz-1对哼唱信号进行高频增强处理,其中μ=0.98.使用汉明窗对哼唱信号片段进行加窗分帧,窗长为 128,其帧间重叠长度设置为64.

对歌曲 《甜蜜蜜》中第 1句简谱为“3563121233”,每个音高占用 1个时间片段,哼唱后按照旋律表示模型生成输入音高模板如图 4所示.

图4 对齐前输入音高模板Fig.4 The input template before alignment

将此模板中的基频F0序列作为遗传算法的输入,根据音符个数(音符个数随输入模板变化,因此也将作为遗传算法的另一参数)取染色体长度为10.种群规模为 40,最大遗传代数 200代,使用代沟0.9,使用基于适应度的重插入算法.从图5中可以看出,经过 20次左右的计算,模板既有收敛的趋势, 40次左右的计算后系统基本稳定.最终得到输出模板与标准模板的相似度为0.999 9.算法迭代过程中具体解的变化和种群均值的变化如图 5所示.

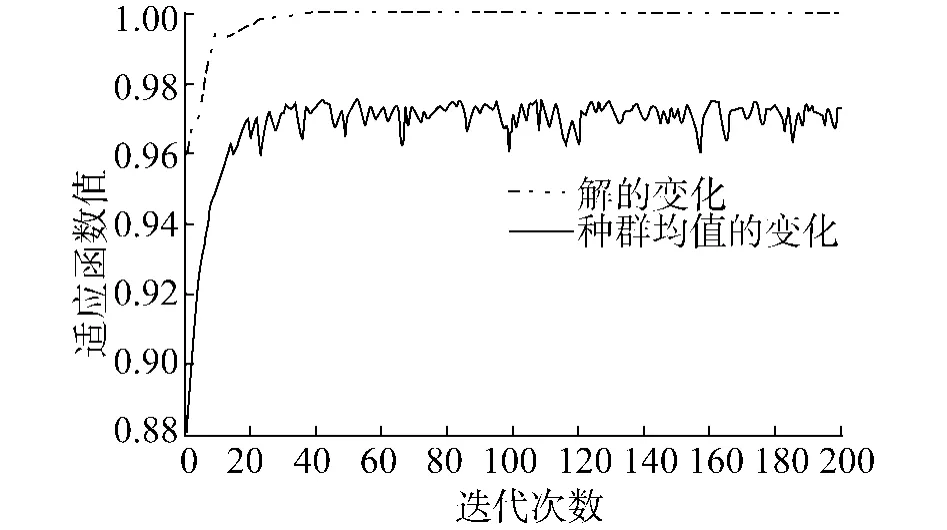
图 5 遗传算法解变化和种群均值变化Fig.5 The solution change and the population'smean value change of the genetic algorithm

在不做归一化的情况下,得出的标逼近模板比输入模板更加接近标准模板.如图 6所示,可以看到经过GA对齐后的模板无论从外形轮廓还是在幅度上都更加接近标准模板.

因为GA的初始种群是随机产生的,在有些训练样本中甚至会产生图 7所示的效果,对齐后的逼近模板与标准模板几乎完全重合,这就意味着对齐后的模板在匹配时将与待匹配样本集中的标准音高模板达到百分之百的相似度,优先被检索出来,这为后续匹配准确率的提高奠定了基础.

图6 GA对齐后模板比较Fig.6 Comparison of the temp late after using GA

图7 逼近模板比较Fig.7 Comparison of the approaching template

最后,将输入模板、逼近模板和标准模板归一化后进行比较,如图 8所示,归一化后逼近模板与标准模板完全重合,这表明经过GA对齐算法,可以使本来并不标准的哼唱输入模板进一步标准化,可以消除不同个体音高上的差异,并且在哼唱不准的情况下,依然可以得到良好检索效果.

图8 归一化后模板比较Fig.8 Comparison of the approaching template after normalization

对40个输入音乐片段检索和比较,采用GA对齐算法使得检索结果优化的占 85%.这说明采用基于遗传算法的轮廓模板对齐,可以促进修正输入音高模板,降低人为哼唱形成的误差,以提高模板精确度,使输入模板和标准模板达到较高的相似度,从而得出更为精确的结果.

4.3 音乐检索系统检索结果及其分析

随机抽取其中20首录制钢琴演奏或管弦乐演奏的音乐片段,相似度由高到底排序.由表 3可知,在乐器发音比较标准的情况下检索前 3位命中率达55%.实验过程中发现命中率与音乐数量成反比,当音乐数量较少,相应模板数量较少的情况下,命中率较高,但当音乐数量增加时,命中率也随之降低.当数据库中音乐量增加时,尽管前 3位的命中率降低,但仍然可以将对应音乐输出到排名靠前的位置,并且考察命中结果的相似度都非常接近.这说明标准音高模板和输入音乐模板之间是相似的,只是由于音乐样本集中的标准音高模板之间本身就非常相似,随着待检索音乐样本集的增大,这些相似的音乐样本对检索的结果就造成了干扰,导致检索结果的排名靠后.2种情况下检索速度基本相同,如果音乐数据库存储在本机情况下,检索结果返回所用时间不到1ms.说明系统相应算法需要较短的检索时间.具体的检索结果如表3所示.

表3 乐器演奏片段检索结果Tab le 3 The retrieval resu lt o f the instrumentation

同样的,对系统中包含的音乐请 5位男女生随机哼唱 20个片段,相似度由高到底排序,从表 4中可以看出,前 3位的命中率与乐器片段相比降低到了10%,但仍然有50%的哼唱片段可以在前 10名命中,这说明,尽管乐器比人哼唱要标准,但是在哼唱不是很标准的情况下系统依然能够获得较好的检索结果.这也说明系统对用户的要求不很苛刻,当用户以自然的方式哼唱时,系统也获得了比较好的容错功能.具体检索结果如表4所示.

表4 哼唱片段检索结果Table 4 The retrieval result of the humm ing

在台湾国立清华大学研究的多模式音乐检索系统中,提出了将输入声波的平均值平移至和歌曲相同,以log(N)的时间内找到最适当的基音[12].这种直接以声波平移的算法相较于本文提出的音高模板所平移的数据量要大的多,假设一段哼唱音乐中包含 10个音符,共有 500帧音乐数据,若以声波平移的方法就要对这 500个数据逐一计算.而根据本文提出的音高模板,只须对 10个音符的音高进行平移,即可得到标准音高基频范围内的逼近模板.

5 结束语

本文主要研究了音乐检索算法中存在的标准模板生成和匹配问题,应用GA算法构造逼近模板,提高模板对齐的速度和精确度;融合动态时间扭曲和欧式距离度量,实现模版自动匹配,增加了匹配的容错机制,增强了系统的健壮性和适应性.但是目前的系统还是在小规模样本上进行的实验,应用遗传算法进行模版匹配.当样本规模比较大的时候,希望应用自动聚类得方法实现样本索引,避免因乐曲数目过大而出现的组合爆炸问题.今后的工作将着重于进一步改进算法,将在用户接口和音乐数据库检索机制上展开研究,以达到大规模音乐数据库的检索要求.

[1]ASIF G,JONATHAN L,DAVID C,et al.Query by humming-musical in formation retrieval in an audio database [C]//Proceedings of the Third ACM International Conference on Mu ltimedia.San Francisco,USA,1995.

[2]CAIR,LU L,ZHANG H J.Using structure patterns of temporal and spectral feature in audio similarity measure [C]//Proceedings of the Eleventh ACM International Conference on Multimedia.Berkeley,2003.

[3]JANG J SR,LEE H R,CHEN JC,et al.Research and developments of a multi-modal MIR engine for commercial app lications in East Asia[J].Journal of the American Society for Information Science and Technology,2004,55 (12):1067-1076.

[4]李 扬,吴亚栋,刘宝龙.一种新的近似旋律匹配方法及其在哼唱检索系统中的应用[J].计算机研究与发展, 2003,40(11):1554-1560.

LIYang,WU Yadong,LIU Baohong.A newmethod for approximatemelody matching and its app lication in query by humming system[J].Journal of Computer Research and Development,2003,40(11):1554-1560.

[5]冯雅中,庄越挺,潘云鹤.一种启发式的用哼唱检索音乐的层次化方法[J].计算机研究与发展,2004,41(2): 333-339. FENG Yazhong,ZHUANG Yueting,PAN Yunhe.A hierarchical app roach to query by humming based on heuristic ru les[J].Journal of Computer Research and Development, 2004,41(2):333-339.

[6]JAY DW.Scale and contour:two components of a theory of memory for melodies[J].Psychological Review,1978,85 (4):341-354.

[7]秦 静,周明全,王醒策.基于动态分割和加权综合匹配的音乐检索算法[J].计算机工程,2007,33(13):194-196.

QIN Jin,ZHOU Mingquan,WANG Xince.MIR app roach based on dynamic thresholds segmentation and weighted synthesismatch[J].Computer Engineering,2007,33(13): 194-196.

[8]PARDO B.Music information retrieval[J].Communication of ACM 2006,49(8):29-31.

[9]刘 建,郑 芳,邓 菁.基于混合幅度差函数的基音提取算法[J].电子学报,2006,34(10):1925-1928.

LIU Jian,ZHENG Fang,DENG Jin.Combined magnitude diference function based pitch tracking algorithm[J].Acta Electronic Sinica,2006,34(10):1925-1928.

[10]UITDENBOGERD A L,ZOBEL J.An architecture for effectivemusic in formation retrieval[J].Journal of the A-merican Society for Information Science and Technolog, 2004,55(12):1053-1057.

[11]ADAMSN H.BARTSCH M A,WAKEFIELD G H.Note segmentation and quantization formusic information retrieval[J].IEEE Transactions on Audio,Speech and Language Processing,2006,14(1):131-141.

[12]许嘉忻,李宏儒,王琼雯,等.由歌曲波形抽取主旋律以进行音乐检索[C]//Proceedings of the Seventh Con ference on Artificial Intelligence and Applications.Taiwan, China,2002.

XU JQ,LI HR,WANG QW,et al.Music retrieval using Melody line extracted from Real-World Music[C]//Proceedings of the Seventh Con ference on Artificial Intelligence and Applications.Taiwan,China,2002.