广义Mycielski图的邻点可区别的非正常全染色

刘利群

(长江大学 信息与数学学院,湖北 荆州 434023)

1 引言

染色问题是图论中具有重要实际意义和理论意义的研究课题之一．本文考虑的图均为没有孤立边,最多有一个孤立点的有限无向单图. 2004年,张忠辅和陈祥恩等人引入了图的邻点可区别的全染色的概念[1],许多学者对图的邻点可区别的全染色的理论作了大量的研究. 2005年,文献[2]提出了图的邻点可区别非正常边色数及全色数(一般邻点可区别色指标)的概念(General neighbour-distinguishing index of a graph).另外,文中一些其他术语及符号参见文献[3].

下面给出一些相关概念:

定义1[1]对阶数至少为2的连通图G(V,E),令f为从V(G)∪E(G)到{1,2,…,k}的映射,其中k为正整数.对任意的u∈V(G),C(u)表示{f(u)∪f(uv|uv∈E(G))}.如果f满足下面的条件

1)对任意的uv,vw∈E(G),u≠v,有f(uv)≠f(vw),

2)对任意的uv∈E(G),u≠v,有f(u)≠f(v),f(u)≠f(uv),f(v)≠f(uv)则称f为图G的一个k-正常全染色.如果f为图G的一个k-正常全染色,并满足

3)对任意的uv∈E(G),有C(u)≠C(v),则称f为图G的一个k-邻点可区别全染色(简记为k=AVDTC).

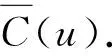
定义2[2]对图G(V,E)，映射F∶E(G)∪V(G)→{1,2,…,k}满足对任意u,v∈V(G)，uv∈E(G)有C(u)≠C(v)，则称f是G的邻点可区别的非正常全染色或一般邻点可区别全染色,简记为gndt-染色.并称gndti(G)=min{k|G有k-gndt-染色}为G的邻点可区别的非正常全色数或一般邻点可区别色指标(general neighbour-distinguishing index of a graph).

定义3[4]设G是顶点集合为V(G)={v0i|i=1,2,…,p}的简单图，n是正整数，称Mn(G)为G上的锥(或广义Mycielski图)，如果

V(Mn(G))={v01,v02,…,v0p;v11,v12,…
,v1p,…,vn1,vn2,…,vnp,w},

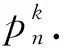
2 主要结果及证明

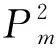
证明 令V(Pm)={v01,v02,…,v0m},E(Pm)={v01v02,v02v03…,,v0(m-1)v0m},

V(Mn(Pm)/{w})={v01,v02,…,v0m,
v11,v12,…,v1m,…,vn1,…,vnm},

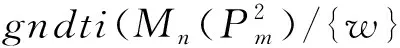
若f(v01v02)=1,f(v02v03)=2,则f(v03v04)=2,f(v03v01)=2,则v01与v02的色集合相同,这与它们是邻点可区别的相矛盾.其他染法类似可推出矛盾.

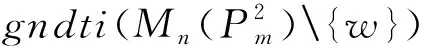
g(vij)=1,i∈{0,1,…,n},j≡1(mod3);
g(vij)=2,i∈{0,1,…,n},j≡3(mod3);
g(vij)=3,i∈{0,1,…,n},j≡0(mod3);

2)再重新给点染色,当g(u)=1时,令f(u)=2;当g(u)=2时,令f(u)=3;当g(u)=3时,令f(u)=1;

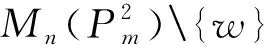
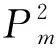
证明 令V(Pm)={v01,v02,…,v0m},E(Pm)={v01v02,v02v03…,,v0(m-1)v0m},

V(Mn(Pm)/{w})={v01,v02,…,v0m,
v11,v12,…,v1m,…,vn1,…,vnm},

当g(vni)=1时,令f(vniw)=2;当g(vni)=2时,令f(vniw)=3;当g(vni)=3时,令f(vniw)=1(i=1,2,…,m).

顶点w可染其中任一颜色.

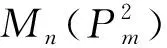
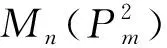
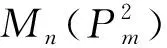
参考文献：

[1]张忠辅,等.关于图的邻点可区别全染色[J].中国科学(A辑),2004,34(5):574-583.

[2]Grorie, Hornak M, Palmer C,et al.General neighbour-distinguishing index of a graph [J].Discrete Mathematics, Special Issue devoted to BBS,2005.

[3] Bondy J A,Murty U S R. Graph Theory with Applications[M].London:Macmillan Press Ltd,1976.

[4] Tardif C.Fraetional chromatic numbers of cones over graphs [J].Graph Theory, 2001,38:87-94.

[5]Zhang Zhong-fu, Liu Lin-zhong, Wang Jian-fang. Adjacent Strong Edge Coloring of Graphs[J].Applied Mathematics Letters,2002,15(5).

[6]刘利群,陈祥恩.路和圈上的锥的D(2)-点可区别正常边染色[J].山东大学学报,2008,43(2):87-97.

[7]Balister P N,Riordan O M,Schelp R H, Vertex-distinguishing edge colorings of graphs[J]. Graph Theory 42,2003,95-109.

[8] Bazgan C,Harkat-Benhamdine A,Li Hao,et al, On the vertex-distinguishing edge colorings of graphs[J].J of Combin Theory,1999,75.

[9]Balister P N, Bollobás B and Schelp R H, Vertex distinguishing colorings of graphs with△(G)=2 [J].Discrete Mathematics, 2002,252.