复杂背景下人脸检测技术的研究*
2010-03-21刘丰年陈迎娜
王 波,刘丰年,陈迎娜
(1.西北大学师资培训中心,陕西西安710127;2.三门峡职业技术学院,河南 三门峡472000)
人脸检测是指在输入的图像中确定出人脸的位置、位姿和尺度。人脸检测技术作为一项人脸信息处理的关键技术,广泛应用在解决模式识别与计算机视觉领域内的实际问题,如人员出入安检、智能人机接口、视觉监视、人机交互和内容检索等[1]。
正因为人脸检测技术在诸多领域应用前景广泛,它作为一项独立的技术课题吸引了来自国际国内著名人脸检测研究机构的众多学者。目前在国内外享誉盛名的人脸检测研究机构主要有:国际方面,主要有美国麻省理工大学的媒体实验室、人工智能实验室和美国卡耐基梅隆大学的智能机器人研究所等[1];国内方面,比较突出的主要有清华大学、上海交通大学等一些知名院校和中国科学院计算所、中国科学院自动化所等部分专业科研院所[2]。
人脸作为一种自然形体属性有很强的共性,但受人的体貌差异、表情变化和采集人脸图像时光照、设备等自然因素的影响,使得图像具有复杂、细致的模式变化,从而也导致了人脸检测过程的复杂化。而已有的人脸检测方法中往往受背景和软件条件的约束,限制了人脸检测技术的应用范围[3]。也就是说,目前还没有一种能够适应各种复杂条件的通用人脸检测技术。鉴于上述情况,找到一种应用于复杂背景下的人脸检测技术是亟待研究的课题。
针对此需求现状,本文提出了一种基于具有形状约束的Snake模型的人脸检测方法。该方法是依据人的脸部轮廓曲线近似于椭圆的特点,将形状能量函数引入Snake模型的能量函数中,进一步加强控制点之间的联系,从而提高复杂背景下人脸检测时收敛结果的准确性。
1 传统的Snake模型
传统的Snake模型是在图像力、内力和外部约束力的共同作用下移动的变形轮廓线:v(s)=(x(s),y(s)),其中s∈[0,1]表示曲线参数,它通过最小化下面的能量函数关系式达到锁定图像特征的目的[2],Econ(v(s))。
1.1 内部能量
轮廓曲线的内部能量函数定义为[4]:

式中vs(s)、vss(s)分别表示曲线v(s)关于s的一阶、二阶导数。一阶导数项vs(s)表示曲线的弹性能量,它控制着曲线的长度和连续性。系数α(s)能够控制轮廓曲线像一个具有弹力、长度变化的绳子以较快或较慢的幅度收缩,系数α(s)的值越小,轮廓曲线在内力的方向上收缩得越慢,故称α(s)为弹力系数。二阶导数vss(s)是指曲线的刚性能量,表示的是活动曲线曲率的变化率,系数β(s)控制着轮廓曲线沿着法线方向朝目标边界运动的速度,轮廓曲线的运动就像一条刚性绳子的运动,在运动的过程中始终保持着原有的光滑和长度不变,β(s)值越小,运动曲线就会变得越柔软,所以称β(s)为强度系数。若使轮廓曲线内部能量Eint最小,轮廓曲线就应当变得的光滑,减小曲率的变化[4]。
理论上讲,只要能够合理地给出轮廓曲线在不同点上α(s),β(s)值,就能够得到目标的任意轮廓。但是自适应地给出这两个权重的值是困难的,通常在工程应用中α(s)和β(s)取常量,即在实际使用中把各点的参数值取为定值,令α(s)=α、β(s)=β。
1.2 外部能量
Eext(v(s))表示外部能量,它是由图像本身的信息和用户的特定限制来决定的,将引导轮廓曲线向目标边缘运动。对于一幅图像I(x,y),传统的外部能量一般定义为[5]:Eext=- │▽I(x,y)│2和 Eext=- │▽(Gσ(x,y)*I(x,y))│2。式中,▽表示梯度算子,Gσ(x,y)则是方差为σ的二维高斯函数。后一个外部能量函数定义与前一个外部能量函数定义相比,它采用了标准偏差为σ的Gauss函数经过低通滤波后的能量,这将进一步扩大能量场的作用范围。同时,从公式中可以得到,梯度最小的地方能量最大,即图像边缘部分的能量最大。
1.3 能量最小化
从上面的论述可以得到:图像轮廓检测被公式化成一个能量函数后,通过求解能量函数的极小值就可以解决人脸检测技术问题。
Kass等人利用变分来求解这一能量函数。那么,Snake模型的总能量就可以写成如下形式[6]:
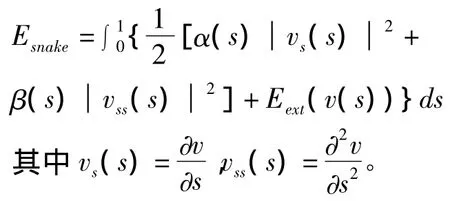
根据变分原理,最小化轮廓曲线能量式,得到欧拉—拉格朗日方程:

写成分量的形式,上式变为:

令 fx(i)= ∂Eext/∂x,fy(i)= ∂Eext/∂yi
为采用数值方法求解,欧拉方程被离散转化为:
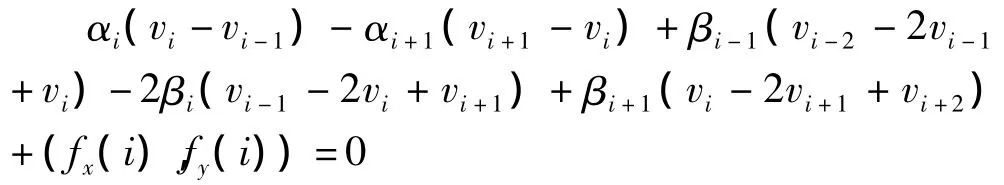
因为 α1=α2=… =αi=α(s)/h2,β1=β2=…βi=β(s)/h4,所以将离散化的欧拉方程变形为关于X和Y的矩阵形式:

式中A为五对角带状矩阵,其阶数由离散点个数来决定。整理以上两个式子可得位置矢量的坐标表达式为:
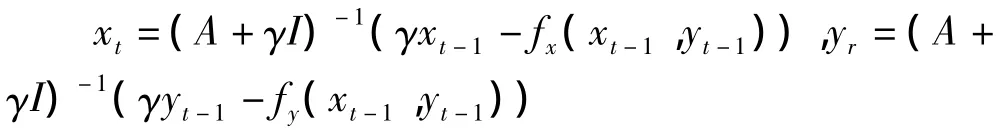
式中矩阵A+γI同样也是一个五对角带状矩阵,γ表示时间步长,它的逆矩阵可用LU进行分解求解。
2 复杂背景下Snake算法的改进
由上述可以知道,传统的Snake模型在演化过程中仅使用了图像的梯度信息,那么在复杂的图像背景下,容易使轮廓线在变化过程中向错误的目标边缘收敛。针对传统Snake模型的缺点,文中根据人脸轮廓曲线近似于椭圆的特点,在Snake的能量函数中加入形状能量项,从而限制了轮廓曲线的形状,提高了Snake模型对复杂背景人脸轮廓提取的准确性。
2.1 能量函数的改进
设Eshape(v(s))为增加的形状能量项,则经过改进的Snake模型能量函数为:
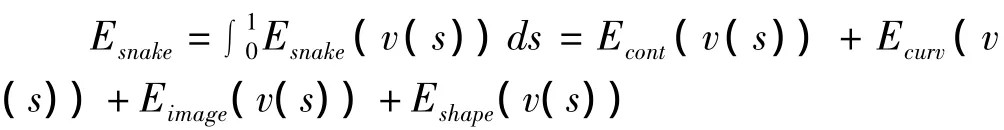
为了构造Eshape(v(s)),根据人脸轮廓曲线近似于椭圆的特点,将N个蛇点进行最小二乘拟合,拟合成一个椭圆。设所拟合的椭圆方程为,其最小二乘解为:y(x)=Ax2+Bx+C。限制形状是为了使Snake线在变形的过程中始终保持近似椭圆形状。其思想可以理解为:轮廓线上的点(xi,yi)在迭代过程中应具有向此拟合的椭圆曲线靠拢的趋势,即(xi,yi)离椭圆曲线越近,Eshape(v(s))越小。所以说,Eshape(v(s))主要取决于轮廓线上的点到曲线y(x)的距离。因此,用这个距离来构造形状能量Eshape(v(s)):

式中di为第i个蛇点到曲线y(x)的距离,dmax,i为第i个蛇点邻域内每个蛇点到y(x)距离的最大值。上述式子表明:第i个蛇点在拟合曲线y(x)上时,该点的形状能量为-1;当第i个蛇点离y(x)的距离较大时,该点的形状能量趋于0;当第i个蛇点到y(x)的距离为dmax,i时,该点的形状能量为0,达到最大。
2.2 改进算法的描述
改进后的Snake模型的能量函数如下:
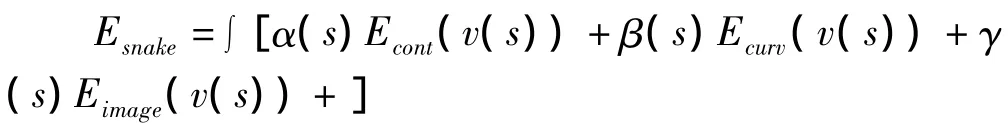
1)弹性能量Econt(v(s))
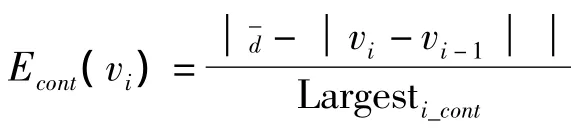
2)刚性能量Ecurv(v(s))

Largesti¯curv表示待考察点某邻域内│vi-1-2vi+vi+1│2的最大值,用于归一化。该能量项则要求轮廓尽可能平滑。
采用Williams等提出的贪婪算法来实现。这种算法认为计算轮廓曲线上各个控制点能量时,其他各点均处于最佳位置,只需计算当前控制点的可能位置。即比较vi与其邻域上像素点的能量函数值,并将其移动到值最小的像素点位置。本文选择的是3×3邻域。
3 实验仿真
利用MATLAB6.5仿真软件实现了如下对比实验:即用传统的Snake算法与本文所提出的算法分别提取同一幅图像的人脸轮廓。图1展示的是一般办公室环境的对比实验,图中背景相对比较复杂,图1(a)所示为传统Snake模型的提取结果,参数设置为α(s)=1.0,β(s)=1.0,γ(s)=1.2,可以看出在复杂背景的条件下,由于轮廓附近的梯度比较复杂,仅使用梯度信息来提取结果偏差较大;图1(b)为本文提出的改进的Snake模型提取结果,引入参数γ(s)=1.6,其他和传统Snake模型所使用的参数一致,由于人脸轮廓受到形状能量的约束,从而获得了比较满意的提取效果。
4 创新点
在原有Snake算法的基础上提出了一种具有形状约束的Snake模型的人脸检测方法,该方法依据人脸形状近似符合椭圆的特征,在Snake模型的能量函数中引入了形状能量函数,使得控制点之间的联系进一步加强,从而提高了复杂背景中人脸检测时收敛结果的准确性。

图1 复杂背景下的人脸检测对比实验
5 结束语
本文主要介绍了一种复杂背景下的人脸检测方法,该方法依据人脸形状近似符合椭圆的特点,在Snake模型的能量函数中引入了形状能量函数,使得控制点之间的联系进一步加强,从而提高了复杂背景中人脸检测时收敛结果的准确性。实验结果表明,该方法具有较好的稳定性,达到了预期效果,这种情况在初始轮廓线附近梯度变化较复杂时尤其如此。但本方法在初始轮廓的选取上需要手工勾勒,因此,为了提高整个流程的自动性,初始轮廓的自动选取还需要进一步的研究。
[1]Moghaddam B,Jebara T,Pentland A.Bayesian Face Recognition[J].Pattern Recognition,2000,33(11):65-74.
[2]冈萨雷斯.数字图像处理(第二版)[M].北京:电子工业出版社,2006.
[3]Lanitis A,Taylor C J,Cootes T F.Automatic face identification system using flexible appearance models[J].Image and Vision Computer,2007,13(5):1-15.
[4]刘正光,刘洁.基于肤色分割的人脸检测算法研究[J].计算机工程,2007,33(4):22-24.
[5]梁路宏,艾海舟,徐光佑,等.人脸检测研究综述[J].计算机学报,2002,25(5):1-10.
[6]宋红,石峰.视频中的多视角人脸检测与姿态判别[J].计算机辅助设计与图形学学报,2007,19(1):90-95.
