有限元静力分析基本原理
2010-03-21郭素娟李江涛
郭素娟, 吴 鸣, 李江涛
1 郑州大学综合设计研究院(450002) 2 核工业第五研究设计院(450052)
0 引言
有限单元法(也称为有限元法)是在当今工程分析中获得最广泛应用的数值计算方法。由于它的通用性和有效性,受到工程技术界的高度重视。伴随着计算机科学和技术的快速发展,现已成为计算机辅助设计(CAD)和计算机辅助制造(CAM)的重要组成部分。
1 有限单元法基本原理
1.1 要点
有限元法的理论是建立在加权余量法和变分原理的基础上的,用有限元法来分析工程或物理问题的要点可归纳如下:
1)将一个表示结构或连续的求解域离散为若干个子域(单元),并通过它们边界上的结点相互联结成为组合体。
2)用每个单元内所假设的近似函数来分片地表示权求解域内待求的未知场变量,而每个单元内的近似函数由未知场函数在单元各结点上的数值和与其对应的插值函数来表达(此表达式通常表示为矩阵形式)。由于相邻单元结点的场函数数值相同,可作为数值求解的基本未知量。因而,求解原来待求场函数的无穷多自由度问题转换成为求解场函数结点值的有限自由度问题。
1.2 一般格式
将二维或三维连续体离散为有限个单元的集合体时,通常要求单元具有简单而规则的几何形状以便计算。常用的二维单元有三角形或矩形,常用的三维单元有四面体、五面体或平行六面体。同样形状的单元还可有不同的单元的结点数,因此单元的种类繁多。如何选择合适的单元进行计算,涉及导求解问题的类型、对计算精度的要求等方面的因素。
1)位移模式的选择
单元中的位移模式一般采用广义坐标为待定参数的有限元多项式作为近似函数,其选取原则可考虑以下几点:
①广义坐标是由结点场变量确定的,它的个数应与结点自由度数相等。如3结点三角形单元有6个结点自由度(结点位移),广义坐标个数应取6个,因此两个方向的位移和各取三项多项式;对于4结点的矩形单元,广义坐标数为8,位移函数可取四项多项式作为近似函数。
②选取多项式时,常数项和坐标的一次项必须完备。位移模式中的常数项和一次项反映了单元刚体位移和常应变的特性。当划分的单元数趋向于无穷大时,单元缩小趋于一点,此时单元应变趋于常应变。
③多项式的选取应由低阶到高阶,尽量选取完全多项式以提高单元的精度。一般来说,对于单元每边有2个端结点的应保证一次完全多项式,每边有3个结点的应取二次完全多项式。若由于项数限制不能选取完全多项式时,选择的多项式应具有坐标的对称性;并且,一个坐标方向的次数不应超过完全多项式的次数,以保证相邻单元交界面(线)上位移的协调性。
2)位移插值函数的建立
在选定广义坐标有限元的位移模式以后,重要的步骤就是建立单元位移场的插值函数表达式。现给出广义坐标有限元的一般步骤和表达式如下:
①以广义坐标为待定参数,给出单元内位移u,则:
u=Φβ
其中,Φ为位移模式,表示位移作为坐标的函数中所包含的项数。
②用单元结点ae~位移表示广义坐标β,惯用的单元结点位移排列是:
ae=[u1v1u2v2…]T
为便于求解广义坐标β,可采用另一种表示方法,如
ae=[u1u2…v1v2]T
将单元结点坐标代入u=Φβ,得到
③将单元结点位移表示单元位移函数u,得到单元插值函数矩阵N。
u=ΦA-1ae~=~Nae~
将结点位移ae~改为一般排列顺序ae,则有
u=Nae
④以单元结点位移ae表示单元应变,并得到应变矩阵B,则:
ε=Lu=Bae
1.3 有限元分析的执行步骤
1)对结构进行离散
按问题的几何特点和精度要求等因素划分单元并形成网格,即将原来的连续体离散为在结点处相互联结的有限单元组合体。
2)形成单元刚度矩阵和等效结点荷载列阵
单元刚度矩阵的一般表达式为:
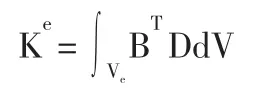
其中,B为应变矩阵,D为材料弹性矩阵,为单元体积。
考虑到单元存在初应力和初应变,单元等效结点荷载列阵的一般表达式为:
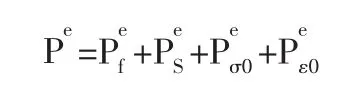
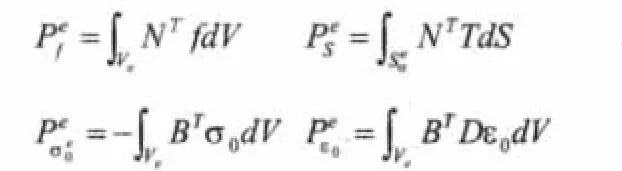
3)集成结构的刚度矩阵和等效结点荷载列阵
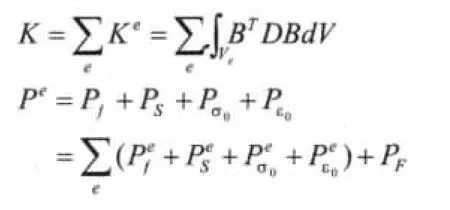
其中,PF为直接作用于结点的集中力。
4)引入几何边界条件
通常几何边界条件(变分问题中为强制边界条件)的形式是在若干结点上给定场函数的值,即:
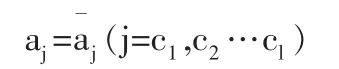
5)求解有限元方程,得到结点位移a
ε=Lu=Bae
6)计算单元应变和应力
ε=Bae
σ=D(ε-ε0)+σ0=DBae-Dε0+σ0
(7)进行必要的后处理。
2 结论
1)用有限元进行分析,可以很精确地得到各个截面的内力和变形,为设计提供参考,这是传统方法不容易做到的。
2)对于更复杂的结构,传统方法需要做大量的简化,造成很大的近似,而有限元能轻松应付,得出比较符合实际的结论。
[1]王勖成.有限单元法[M].北京:清华大学出版社,2003
[2]曾攀编著.有限元分析及应用[M].北京:清华大学出版社,2004
