城轨车辆客室侧顶板气动撑杆的设计
2010-03-21姜云海
姜云海
(南车青岛四方机车车辆股份有限公司技术中心,266111,青岛∥工程师)
城轨车辆客室侧顶板气动撑杆的设计
姜云海
(南车青岛四方机车车辆股份有限公司技术中心,266111,青岛∥工程师)
作为客室侧顶板开闭的辅助装置,气动撑杆在城轨车辆上的应用越来越广泛。然而,气动撑杆固定支点位置的确定和主要技术参数的选择一直是设计的难点。从侧顶板的开闭过程机理入手,通过力学和运动学分析,摸索出了气动撑杆的设计准则,并通过辅助几何建模和计算的方法,快速地确定出气动撑杆的固定支点位置和主要技术参数。通过设计实例对设计方法进行了验证。
城轨车辆;侧顶板;气动撑杆
Author's addressCSR Qingdao Sifany Locomotive and Roling Stock Co.Ltd.,266111,Qingdao,China
城轨车辆客室侧顶板内部一般都设置了侧门机构、电子地图、扬声器、门控器等需要经常检修的设备。传统侧顶板设计中没有设置气动撑杆,维修人员检修时,需要人工托住侧顶板,劳动强度大且效率低。近年来,气动撑杆以其操作轻便、运行平稳的特点成功运用到客室侧顶板上。由于气动撑杆能帮助侧顶板实现自动开启和手动关闭功能,因此,受到了越来越多城轨车辆用户的青睐。然而,气动撑杆的固定支点位置及技术参数受设计结构影响较大,用常规设计办法很难把握。本文从力学和运动学方面入手,通过分析计算,摸索一种快速确定气动撑杆支点固定位置和选择主要技术参数的方法。
1 侧顶板开闭过程机理
1.1 气动撑杆简介
气动撑杆是一种可通过气缸内气体体积的变化来控制活塞杆伸展和压缩的设备,包括气缸、活塞杆、端部接头、密封件等部件。气动撑杆的结构外形如图1所示。

图1 气动撑杆结构外形示意图
1.2 侧顶板自动开启机理
从运动和动力学的角度分析,在不考虑摩擦力时,侧顶板只受到重力矩和气动撑杆的推力力矩作用。
·当打开锁闭机构后,重力矩大于撑杆力矩,侧顶板沿着重力矩的方向自动开启;
·当侧顶板开启到一定角度后,重力矩变为零,侧顶板沿着撑杆力矩的方向继续开启;
·当侧顶板开启到规定角度后,重力矩与撑杆力矩相等,但方向相反,侧顶板停止继续开启。
1.3 侧顶板手动关闭机理
当关闭侧顶板时,用手按压提供关闭力矩,克服撑杆和重力共同作用产生的开启力矩,侧顶板逐渐关闭,达到锁闭位后利用锁闭机构将侧顶板进行限位固定。
2 几何位置对准静态气动撑杆力矩的作用
根据侧顶板的开闭过程机理和初步设计结构,可建立气动撑杆的受力分析模型(见图2)。
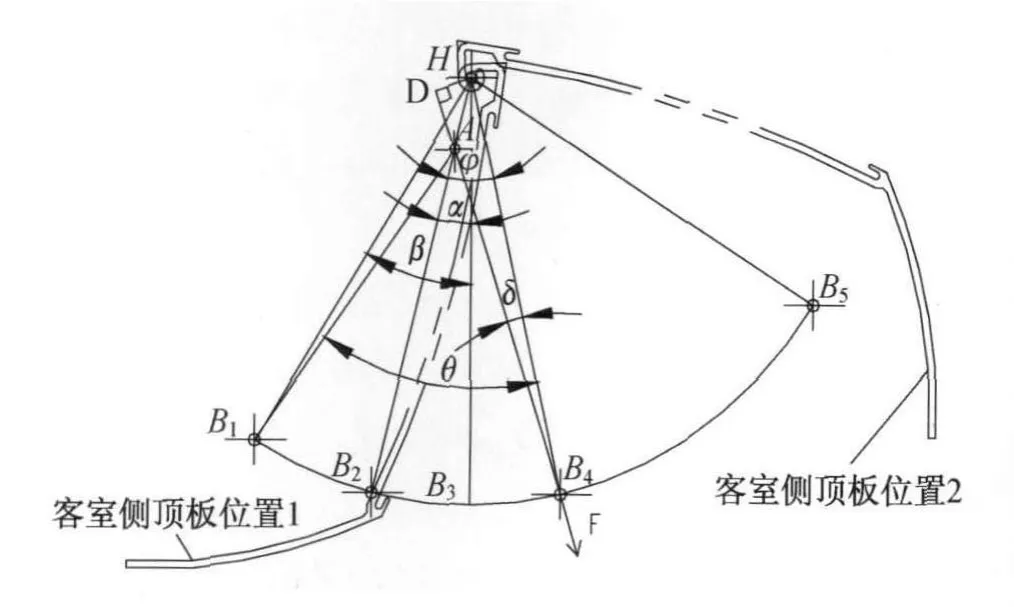
图2 气动撑杆受力分析模型
图2中:
H——侧顶板固定铰接点;
A——气动撑杆的安装支点;
B1——气动撑杆在侧顶板上的安装支点;
B2——气动撑杆力矩零位;
B3——气动撑杆垂直位;
B5——气动撑杆规定最大开启位;
α——H A与HB3的交角;
β——AB1(关闭位置)与 HB3的交角;
θ——侧顶板开度角。
假设B4点是侧顶板任意开启位置时气动撑杆的受力位,φ为H A与HB4(开启位置)之间的夹角,δ为HB1与 HB4(开启位置)之间的夹角。
根据图2及上述参数可计算出撑杆作用力臂及反作用力矩Mb。
假设H A=a,HB4=HB1=b,AB4=c,HD=d;则:
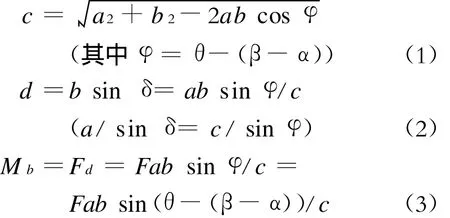
从式(3)可以看出,Mb是F 、a 、b、c、θ、α、β的函数,变化关系比较复杂,必须根据其与重力力矩之间的相互约束关系来确定气动撑杆的固定位置。
3 几何位置对重力矩作用
根据侧顶板的初步结构设计和设计要求的侧顶板最大开启角度θmax,可建立侧顶板重力受力分析模型(见图3)。
图3中:
H——侧顶板的转轴位置;
C1——侧顶板关闭位重心位置;
C3——重力矩零点位置;
C4——侧顶板最大开启位重心位置。
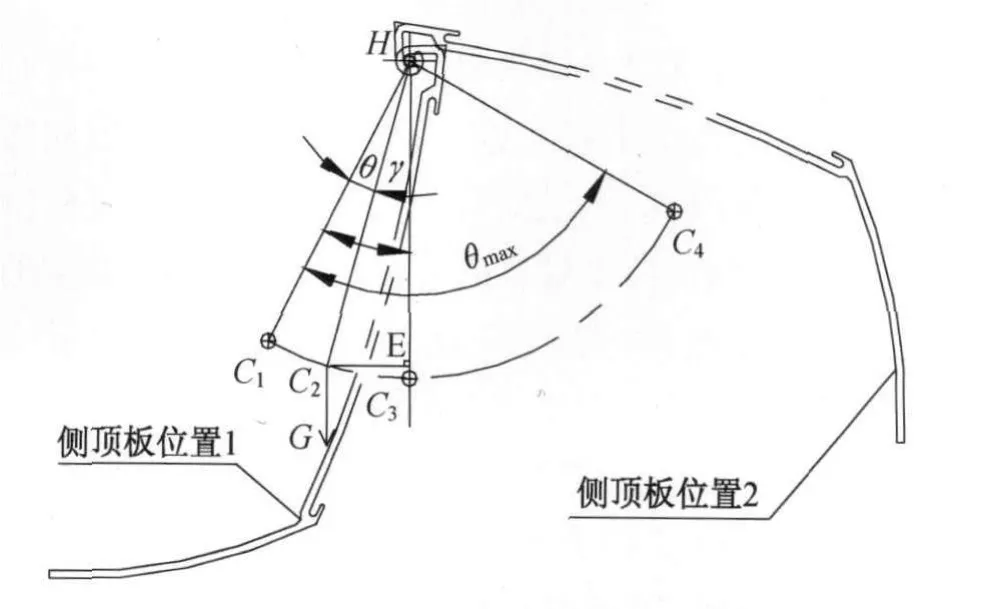
图3 重力受力分析模型
假设C2是侧顶板开启任意几何位置时的重心,根据图3,可计算出重力产生的力矩Mc。
假设HC2=L,EC2=h,γ是侧顶板转轴位置H与C1、C3的交角,θ为侧顶板转轴位置 H 与C1、C2的交角。
则:

式中:
γ、L ——常数;
θ——侧顶板开度角,可随侧顶板的开闭变化(一般情况下,θ的取值范围从0~90°)。
从式(4)可以看出,Mc是θ的函数:在 θ的取值区间内,当 θ<γ时,Mc>0,重力产生逆时针方向力矩;当 θ=γ时,Mc=0,重力力矩为零;当 θ>γ时,Mc<0,重力产生顺时针方向力矩。
4 气动撑杆设计准则
(1)刚打开侧顶板锁闭机构时,气动撑杆推力力矩不能阻碍侧顶板开启。打开锁闭机构后,侧顶板在重力矩作用下可实现自动开启。此时,气动撑杆的推力力矩不能大于重力产生的逆时针方向力矩;同时,为了防止侧顶板开启力矩过大,尽量将气动撑杆的推力力矩设计成与重力矩相反的方向,即顺时针方向。
(2)当侧顶板重力力矩减小为零时,气动撑杆推力力矩应产生开启力矩。当侧顶板开启到C3位置时,重力力矩变为0,侧顶板失去了开启力矩。因此,为了保证侧顶板继续开启,应将该位置气动撑杆的推力力矩设计成开启力矩,即逆时针方向力矩。
(3)气动撑杆推力力矩零点位置应设计在HC1与HC3之间的区域。根据上述(1)、(2)分析可知,气动撑杆推力力矩从关闭位置到C3位置应有一个方向变化,即从顺时针方向变化为逆时针方向。
(4)当重力力矩阻碍侧顶板开启时,气动撑杆推力力矩应大于重力力矩。在侧顶板开启位置超过重力矩零点位置C3之后,重力产生阻碍侧顶板继续开启的力矩;为了保证其继续开启并达到规定的最大开启角度,气动撑杆推力力矩必须大于重力力矩。
(5)气动撑杆推力力矩不能大于侧顶板设计最大开度角度位置的重力矩。侧顶板运行到规定的最大开启角度时,需要保持静态平衡。因此,气动撑杆推力力矩不能过大,否则会破坏侧顶板。
5 气动撑杆固定位置的确定及参数核算
5.1 气动撑杆固定位置的确定
由于气动撑杆的主要功能是保证侧顶板自动开启和定位,因此,不妨假设侧顶板开启方向力矩为正方向力矩,那么阻碍侧顶板开启方向的力矩就为负方向力矩。
根据上节(1)和式(3)可知,在侧顶板关闭位置Mb<0,即当 θ=0时,β>α;也就是说 HB1应设计在 HA的左侧。根据上节(1)和式(3)、(4)可知,在重力矩的零点位置,Mb>0,Mc=0。即可得:当θ=γ时,β<γ+α。
当侧顶板的结构设计完成后,γ为常数,因此可得:0<α<γ(α在HC1与 HC3之间的区域),α<β<γ+α。
根据上述分析,再结合侧顶板具体设计结构和侧门机构空间关系,利用二分法和一定的假设即可将气动撑杆的固定位置A点和B点确定下来。
5.2 撑杆工作行程和推力计算
5.2.1 气动撑杆工作行程
气动撑杆工作行程是指气动撑杆活塞杆从伸展状态压缩到最小安装尺寸时的轴向位移,即工作行程
根据式(1)和图2可知:当θ=β-α时,c=cmin;当 θ=θmax时 ,c=cmax。假设 AB5=S2,AB2=S1,气动撑杆工作行程:

5.2.2 气动撑杆公称力
气动撑杆公称力Fa是指气动撑杆最小伸展力和最小压缩力的平均值。由于本文忽略活塞与气缸之间的摩擦力,因此,公称力Fa是指活塞杆处于最大伸展状态时测得的伸展力Fmin。
由于撑杆固定位置区域已经确定,不妨假设α=γ/2,β =γ,HA=a(常数),HB1=b(常数);同时 ,根据上节(5),当θ=θmax时,Mb=Mc;可得气动撑杆公称力
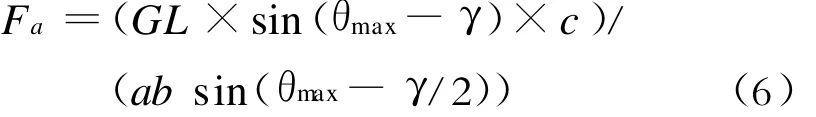
5.2.3 气动撑杆推力
由于活塞与气缸之间的摩擦力一般较小,可忽略不计,因此可以假设气动撑杆的最小伸展力和最小压缩力相等,最大伸展力和最大压缩力相等。因此气动撑杆的推力-行程特性曲线可简化为如图4所示,于是可得撑杆推力

其中,K为常数,主要受气动撑杆气缸内径、活塞杆外径、气缸内工作介质等因素影响,由生产厂家根据设计要求及相关标准确定。
结合式(5)、(6)可得任意位置撑杆推力

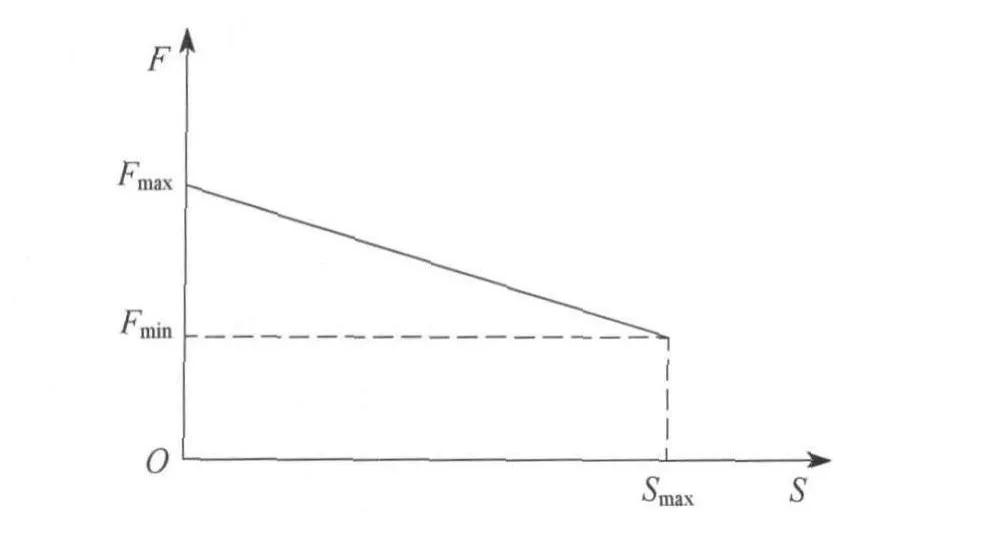
图4 F与S之间的关系
6 气动撑杆结构核算与验证
气动撑杆的固定位置区域确定后,需要对气动撑杆关门力矩进行验证,以确定气动撑杆设计是否合理。
根据式(1)、(4)、(7)做出ΔM与θ的关系曲线(见图5)。ΔM越小,气动撑杆作用效果越好。
ΔM如果太大,一方面说明侧顶板开启力矩较大,开启速度会较快,容易伤人;另一方面说明侧顶板受力状态不佳,不利于侧顶板的安装及缝隙调整。此时需要重新设计气动撑杆的固定支点位置,直到单人可以轻松关闭侧顶板。
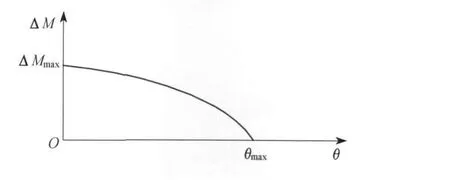
图5 开启力矩ΔM与开度角θ之间的关系曲线
7 气动撑杆设计运用实例
根据上述分析与计算,可以快速完成北京地铁4号线侧顶板气动撑杆的设计。具体设计步骤如下:
侧顶板初步设计结构完成后,可以确定出下列数据 :重力 G=150 N,夹角 γ=8°,HC1=120 mm,最大开启角度 θmax=66°(变化范围 0~66°)。根据式(4)可以计算出Mc max=11082 N·mm。
利用二分法确定气动撑杆固定支点位置。由于0<α<γ,α<β<γ+α,可假设 α=γ/2=14°,β=γ=28°;同时根据边界条件,进一步假设HA=a=40 mm,HB1=b=160 mm,则根据式(6)可计算出气动撑杆公称力Fa=152 N;根据式(1)及式(5)可计算出气动撑杆工作行程S=19 mm。
根据式(3)、(4)及上述已知条件,可做出开启力矩ΔM与θ的关系曲线。对该曲线图进行分析计算后可知:Δ Mmax约为 4650 N·mm,而关闭侧顶板时,手推力的作用力臂约为160 mm。因此只需要不大于30 N推力即可关闭侧顶板,满足气动撑杆关门力矩不宜过大的设计要求。
目前,该气动撑杆已经成功运用到北京地铁4号线车辆上,经实际运用验证,效果良好。
8 结语
在侧顶板气动撑杆设计过程中,由于侧顶板所受重力力矩和气动撑杆的推力力矩都随侧顶板不同的开度而变化,用常规方法很难设计出完全满足设计要求的气动撑杆。本文从力学和运动学方面入手研究,从各种变化中找出重力力矩和气动撑杆推力力矩二者之间的内在联系,并通过几何建模和力学分析,快速准确地确定出了气动撑杆的固定支点位置和公称力、工作行程等技术参数。
[1]周衍柏.理论力学教程[M].北京:高等教育出版社,2007.
[2]黄天泽,黄金陵.汽车车身结构与设计[M].北京:机械工业出版社,1992.
Design and Development of Stay Bar in Urban Railway Vehicle
Jiang Yunhai
As an auxiliary part of the side roof's action(on or off),the pneumatic stay bar has been used widely on rail transit vehicles.However,to define the fixed location and the main technical parameters of the stay bar is still difficult.This article uses both mechanics and kinematics analysis to design the stay bar,defines its location and the main technical parameters quickly with methods of geometry modeling and calculation,and finally verifies the design principles through a practical design example.
urban railway vehicle;side roof;pneumatic stay bar
U 270.38
2009-02-17)
