图像去噪LOT模型的分裂Bregman方法*
2010-03-19庞志峰杨余飞
庞志峰,杨余飞†,林 玲
(1.湖南大学数学与计量经济学院,湖南长沙 410082;2.广东外语外贸大学信息科学技术学院,广东广州 510420)
由于图像在生成、存储或者传递过程中经常被噪声污染,因此图像去噪是图像处理中的一个最基本的问题.随着计算机技术的不断进步,最近20年来,基于偏微分方程(PDE)的图像去噪方法得到了很快的发展[1-2].传统的PDE去噪方法主要是滤除图像的高频成分,然而由于图像的细节也分布在高频区域,所以总是在滤除噪声的同时模糊了图像的边缘.为了能在滤除噪声的同时也能保持图像的边缘,Rudin等[3]提出了如下的全变分(Total Variation)去噪模型(ROF模型):

式中:Ω∈R2,u为待修复的原始图像,f为噪声图像,为正则化因子.然而,全变分正则化模型经常在图像恢复过程中出现阶梯现象.为了克服阶梯现象,文[4-6]考虑下面的高阶PDE去噪模型(LLT模型):
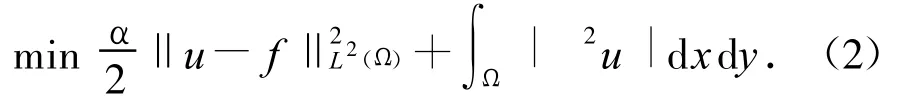
式中:为正则化因子.但是由于高阶PDE演化图像的边缘比全变分模型快,所以经常在图像的边缘引起模糊现象.
为了在去除噪声的同时不但保持图像的边缘,而且避免阶梯现象,Lysaker等[7]建议下面的两步算法(LOT模型):
第1步:令n=(n1,n2)拟合噪声图像的法向量,即:
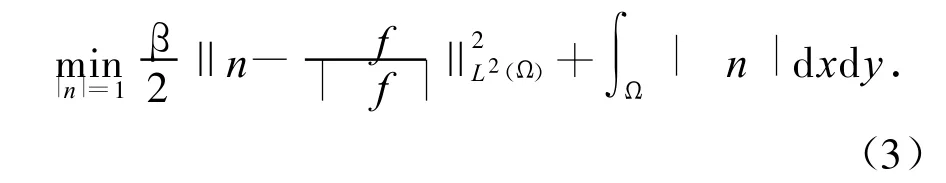
第2步:令n0=(n0x,n0y)为式(3)的解,求解下面的优化问题:
事实上,式(4)和式(1)以及式(2)含有的L1项使得数值求解并不容易,从而寻求有效的数值解法解此类问题是当前的一个重要研究内容.最近,基于Bregman迭代算法,Goldstein和Osher[8]建议用分裂Bregman方法解带有L1项的图像恢复问题.由于此算法具有编程简单、数值求解过程比较稳定、在计算过程中保持正则化参数为一个常数、占有内存小且具有较快的计算速度和收敛速度等优势,广泛应用于图像恢复问题[8-11].因此,基于分裂Bregman方法能有效地处理含有L1项的优化问题,本文提出用该方法来解LOT去噪模型的第2步,也就是优化问题(4).
1 图像去噪LOT模型的分裂Bregman算法
分裂Bregman方法由于能有效处理含有L1项的优化问题并且在数值求解过程中比较稳定,因此最近被广泛应用到图像复原、图像修补、图像压缩等领域.本节首先回顾文献[8]中的分裂Bregman方法,然后提出用该方法来解LOT去噪模型的第2步式(4),并给出具体的算法.
1.1 分裂Bregman算法
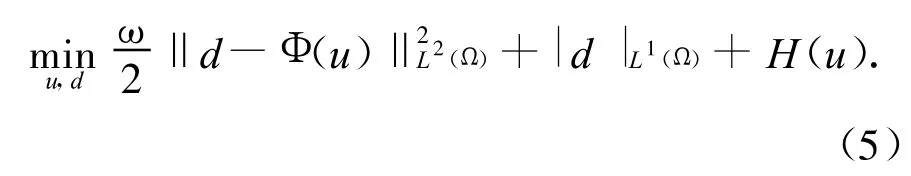
式中:ω为正则化参数.很明显,问题(5)在一定条件下等价于下面的约束优化问题:
考虑下面的优化问题
对于式(5),由于含有两个变量u,d,因此利用文[9]中的思想,引入一个辅助变量c可以通过下面的交替算法求解:
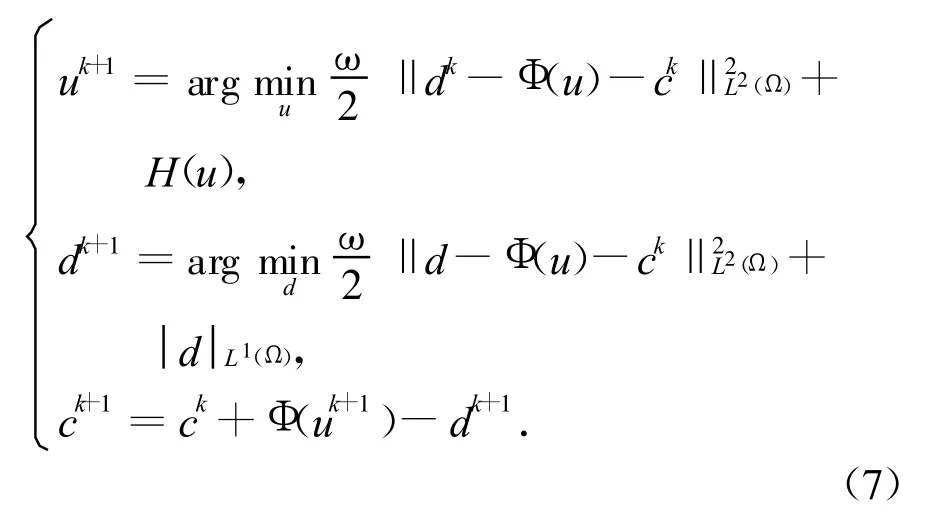
所以,我们有下面的分裂Bregman算法解优化问题(7).
算法1 分裂Bregman算法
步0 取初值u0=f,d0=0,c0=0,令k:=0;
步1 计算式(7)求得(uk+1,dk+1,ck+1);
步2 若终止条件满足,则停止;否则,令k:=k+1,转步1.
注 在算法1中,一般情况下H(u)为连续可微的,因此我们可以直接求出式(7)的第1个子问题的欧拉方程,然后利用一般的数值方法求解.然而虽然式(7)的第2个子问题不可微,但是该问题是严格凸问题并且含有一个不可微项|d|L1(Ω),因此在求欧拉方程时,我们需要用到广义导数.经过简单的计算并引入阈值算子有:
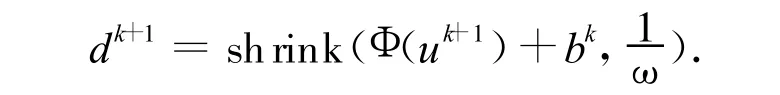
其中:

1.2 LOT模型的分裂Bregman方法
由于LOT模型的第1步(3)中含有1个等式约束|n|=1,使得求解并不容易,因此文[7]中引入一个辅助变量θ,使n=(nx,ny)=(cos θ,sin θ).另一方面,由于|n|=|θ|,因此若令n:=(,)=则问题(3)可转化为下面的无约束问题:

进一步,式(8)对应的欧拉方程为:

利用下面的事实:
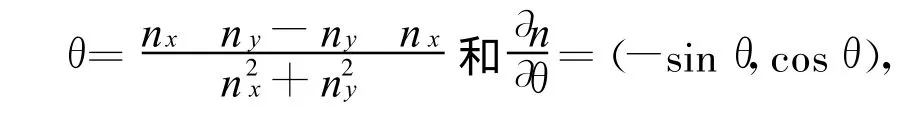
文[7]中建议解下面的稳态方程


现在考虑LOT模型的第2步,若令n0=(nx,ny)且设H(u)=‖u-f‖(Ω),并引入辅助变量d=u,类似于1.1节的分裂Bregman迭代算法,优化问题(4)可写成如下类似式(7)的形式:
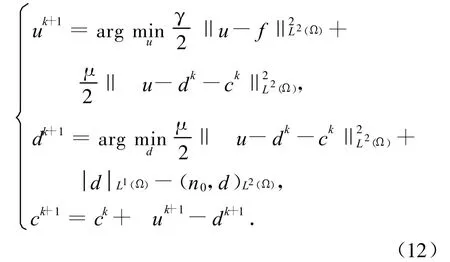
事实上,式(12)和式(7)的第2个优化问题有所不同,很明显,在式(12)中,(n0,d)L2(Ω)+‖u-dk-ck‖关于d是可微的.因此结合式(10)和式(11)以及算法1,对图像去噪LOT模型,我们提出下面的分裂Bregman算法:
算法2 图像去噪LOT模型的分裂Bregman算法.
第1步:利用半隐式时间演化法式(10)和式(11).
步0 取初值n0=(,),令k:=0;
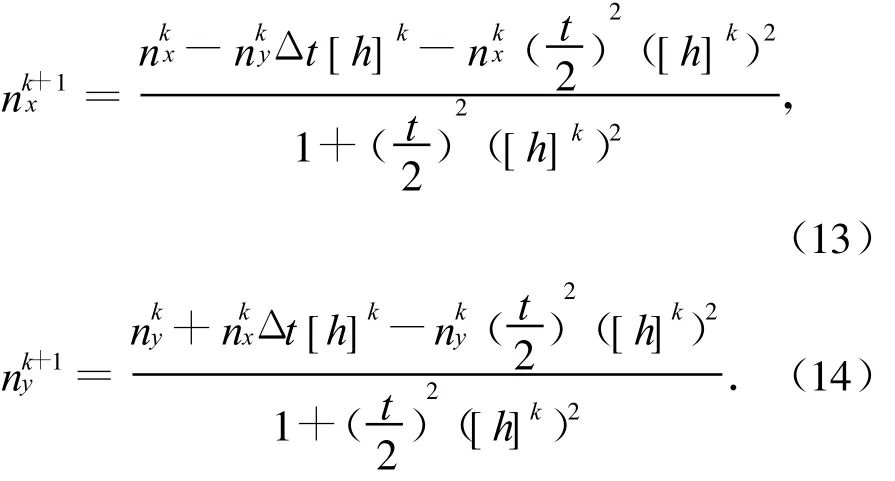
其中Δt为时间步长
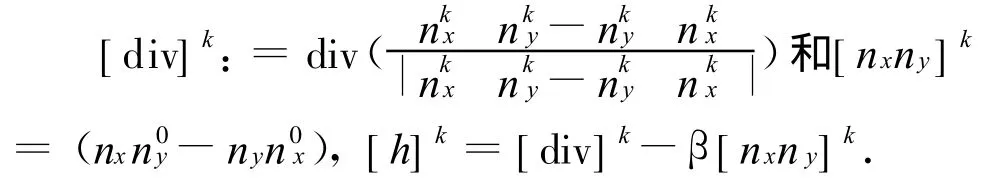
第2步:利用分裂Bregman算法(12).
为获得T-Map的3维空间域,依次将规范重心坐标λF表达式中限定自由度方向的和设定为“0”,实现T-Map维数由4维降为3维。
步1 取初值u0=f,d0=0和c0=0,令k:=0;
步2 通过解式(15)~式(19),计算(uk+1,dk+1,ck+1):

其中:

步3 若停止准则满足,则算法停止,输出复原图像u;否则,令k:=k+1,转步2.
注:事实上,算法2中的式(18)对应式(15)的第1个式子且对应的欧拉方程为:

其中:I和Δ分别为单位算子和Laplace算子.因此在离散情况下,我们可以用Gauss-Seidel迭代:

具体算法流程图如图1所示.
2 实验结果及其评价
本节进行相关的数值试验来说明所提出算法的有效性.实验平台为:Intel core(TM)2 DUO CPU,2.20 GHz,2G内存,Windows XP操作系统,Matlab7.5软件.
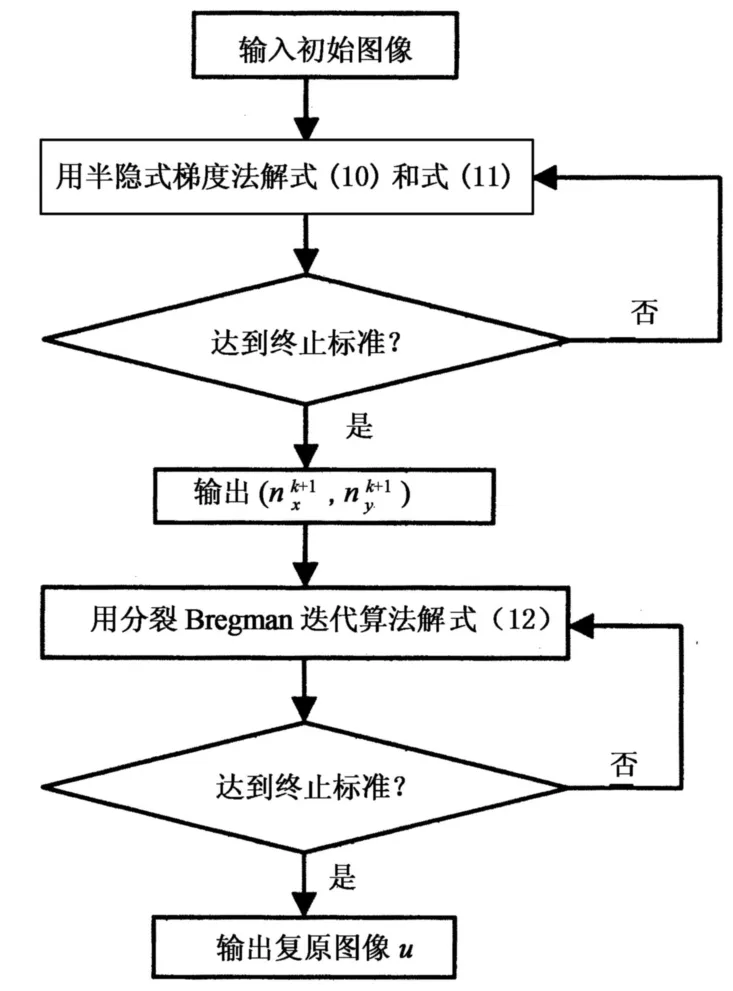
图1 算法2流程图Fig.1 The flow diagam of algorithm 2
首先我们比较LOT模型与经典的ROF模型以及LLT模型的去噪效果.考虑添加标准差为10的高斯白噪声的Lena图像面部(图2(a)和图2(b)).

图2 Lena图像面部Fig.2 The face of lema image
由于Lena图像的面部含有平滑区域,因此在使用ROF模型去噪时经常出现阶梯现象.另一方面,由于图像的边缘区域出现图像像素值的跳跃,因此在使用LLT模型去噪时这些区域经常出现模糊.为了更好地比较这3种模型,对于ROF模型(1)以及LLT模型(2),我们建议用文[3,6]的半隐式梯度下降法,其中相关的正则化参数和时间步长t依次为:λ=0.08,tROF=0.02和α=0.275,tLLT=0.075.对于LOT模型的第1步,我们取正则化参数β=1.125和时间步长t=0.08;在第2步中,我们建议用分裂Bregman算法,其中γ=0.115,μ=0.002.若设定迭代次数为200次,则从图2中可以看出LOT模型复原的图像(e)在一定程度上克服了ROF模型复原图像(c)中的阶梯现象,又能避免LLT模型复原图像(d)中的边缘模糊现象,尤其是在图像中帽檐区域.为了更好地理解这3种模型的复原效果,我们绘出了复原图像与噪声图像的差.很明显,如图2所示(e1)同时具有(d1)和(c1)的特征.
下面我们比较文[7]中的算法和本文提出的分裂Bregman算法,考虑添加方差为12的白色高斯噪声的Cameraman图像(图3).Cameraman图像中不但含有像素跳跃区域(如:相机支架),而且也含有图像渐变区域(如:天空).对于LOT模型的第一步:法向拟合步,我们仍然用文[7]中的半隐式梯度下降法,其中相关的参数依次设定为β=1.125和时间步长t=0.1,迭代次数为300次.现在考虑复原图像步,即:LOT模型第2步,其中正则化参数γ=0.135.设定文[8]中的用梯度下降法(GD)解式(4)的时间步长t=0.1,用分裂Bregman方法解(4)的正则化参数μ=0.004,若相邻两次迭代结果满足8.25×10-4,则第2步迭代终止.

图3 Cameraman图像Fig.3 Cameraman image
如图3所示,两种算法几乎有着同样的复原结果.另外,从表1中可以看出这两种算法在满足终止标准时,文[7]中的原始梯度下降法需要57次迭代,大约耗时2.890 6 s,而分裂Bregman迭代算法仅仅需要27次迭代,耗时大约1.828 1 s.另外,从收敛曲线图中(图4)可以看出分裂Bregman方法有着较快的收敛速度.同时还可以看出此时分裂Bregman方法有着较好的修复效果.

表1 实验Cameraman的相关结果Tab.1 The pelated results of cameraman experiments
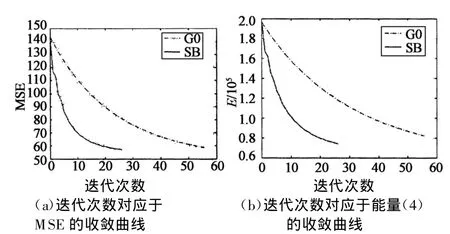
图4 收敛曲线Fig.4 Convergence carves
3 结 语
由于分裂Bregman方法能有效地处理含有L1项的优化问题,因此本文利用分裂Bregman方法来处理LOT模型的第2步.实验结果表明,与传统的梯度下降法相比较,该方法不但有着较快的收敛速度,而且也能保持图像的平滑区域和边界区域的信息.另外,由于LOT模型的第1步含有一个等式约束,因此值得进一步研究有效地处理第1步的数值方法.
[1] CHAN T,SHEN J.Image processing and analysis:Variational,PDE,wavelet and stochastic methods[M].SIAM,2005:145-198.
[2] A UBERT G,KORNPROBST P.Mathematical problems in image processing:partial differential equations and the calculus of variations[M].New York:Springer Verlag,2002:67-136.
[3] RUDIN L,OSHER S,FAT EMI E.Nolinear total variation based noise removal algorithms[J].Physica D,1992,60:259-268.
[4] STEIDI G.A note on the dual treatment of higher order regularization functionals[J].Computing,2006,76:135-148.
[5] SETZER S,STEIDI G.Variational methods with higher-order derivatives in image processing[C]//Brentwood Approximation,Nashboro Press,2008,12:360-386.
[6] LYSAKER M,LUNDERVOLD A,LUNDERVOLD,et al.Noise removal using fourth-order partial differential equation with applications to medical magnetic resonance images in space and time[J].IEEE T rans Image Process,2003,12:1579-1590.
[7] LYSAKER M,OSHER S,TAI X.Noise removal using smoothed normals and surface fitting[J].IEEE T rans Image Proce,2004,13(10):1345-1357.
[8] GOLDSTEIN T,OSHER S.The split Bregman for L1 regularized problems[J].SIAM Jornal on Imaging Sciences,2009,2(2):323-343.
[9] CAI Ji,OSHER S,SHEN Z.Split Bregman methods and frame based image restoration[R].UCLA CAM:Report,2009:9-28.
[10]TAI X,WU C.Augmented lagrangian method,dual methods and split Bregman iteration fo r ROF model[R].UCLA CAM:Report,2009.
[11]SETZER S.Split bregman algorithm,Douglas-Rachford splitting and frame shrinkage[C]//Scale Space and Variational M ethods in Computer Vision,Berlin:Springer,2009,5567:464-476.
