基于LMD和AR模型的转子系统故障诊断方法*
2010-03-19杨丽湘程军圣
杨 宇,杨丽湘,程军圣
(湖南大学汽车车身先进设计制造国家重点实验室,湖南长沙 410082)
当转子系统发生故障时,由于系统载荷、刚度等多方面的影响,其振动信号多表现为复杂的非平稳信号[1].如何从非平稳信号中提取特征向量是转子系统故障诊断的关键,传统的故障诊断技术通过分析并提取振动信号时域或频域波形的特征量,建立判别函数来识别转子系统的工作状态.但是,对于非平稳信号,很难仅通过时域或频谱分析来对转子系统的工作状态做出较为准确的评价.
AR模型的自回归参数凝聚了系统状态的重要信息,对系统状态变化规律反映较敏感[2],因此可以采用AR模型的自回归参数作为特征向量来分析系统的状态变化.然而,AR模型只能适用于平稳信号的分析,因此需要在建立AR模型之前对信号进行预处理.目前较多的文献采用EMD(Empirical Mode Decomposition)方法对原始信号进行分解,然后对分解得到的各个分量分别建立AR模型,以提取特征向量[3-4].但是,EMD方法理论上还存在一些问题,如过包络、欠包络、模态混淆、端点效应和由于Hilbert变换产生的无法解释的负频率等,这些问题目前仍在研究当中[5-6].
局部均值分解法是由Jonathan S.Smith提出的一种新的自适应时频分析方法[7],它能将一个复杂的非平稳信号分解为若干个PF分量之和.每一个PF分量都由一个包络信号和一个纯调频信号相乘得到,因而它是一个瞬时频率具有物理意义的单分量的调幅-调频信号,很好地反映了原始信号的真实信息,从而可以进一步对每一个PF分量分别建立AR模型.同时,相对于EMD方法,LMD方法在抑制端点效应、减少迭代次数和保留信号信息完整性等方面要优于EMD方法[8].基于上述分析,本文提出了基于LMD和AR模型的转子系统故障诊断方法,首先采用LMD方法将转子系统振动信号分解为若干个PF分量之和,然后对各个PF分量分别建立AR模型,采用AR模型的自回归参数和残差方差作为特征向量,进一步采用神经网络分类器对转子系统工作状态和故障类型进行分类.对具有不对中、不平衡、油膜涡动故障和正常状态下的转子系统振动信号的分析结果表明,将LMD和AR模型相结合能有效地应用于转子系统的故障诊断,从而为转子系统的故障诊断提供了一种新的方法.
1 LMD方法
LMD分解法实际上就是把信号分解成不同尺度的包络信号和纯调频信号,将包络信号和纯调频信号相乘便可以得到具有瞬时物理意义的PF分量,然后获得信号的时频分布.对任意信号x(t),其PF分量可按以下方法获得[7].
1)确定信号x(t)的所有局部极值点ni.
2)通过各极值点ni,计算两相邻极值点ni和ni+1的平均值mi和包络估计值ai:

3)将各相邻的局部均值mi和包络估计值ai用直线相连,用滑动平均法进行平滑处理得局部均值函数m11(t)和包络估计函数a11(t).
4)将局部均值函数m11(t)从原始信号中分离出来,并通过包络估计函数a11(t)对所得结果进行解调,得调频信号s11(t).
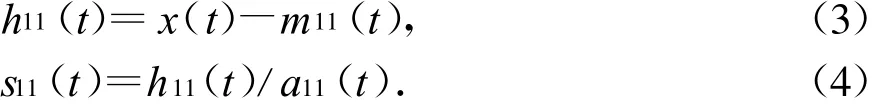
判断s11(t)是否为一个纯调频信号,判断条件是它的包络估计函数a12(t)是否满足a12(t)=1,若条件不满足,则将s11(t)作为原始信号重复上述过程,直到得到纯调频信号s1n(t)为止,如此循环有:

式中:

迭代终止条件为:

在实际应用中,为了减少迭代次数,降低运算时间,可设置一个变量Δ,使得当满足条件1-Δ≤a1n(t)≤1+Δ时,迭代终止.
5)将迭代过程中所产的全部包络估计函数相乘,得包络信号(瞬时幅值函数):

6)将包络信号a1(t)和纯调频信号s1n(t)相乘得:

它为信号x(t)的第一个PF分量,包含了原始信号的最高频率成分,是一个单分量的调幅-调频信号,瞬时频率f1(t)则可由纯调频信号s1n(t)求出:

7)从原始信号x(t)中将第1个PF分量PF1(t)分离出来,得到剩余信号u1(t).由于剩余信号u1(t)中还含有较多的频率成分,因此将u1(t)作为原始数据重复以上步骤对其进行分解,得到第2个PF分量,重复这个过程直到uk为一个单调函数为止,如此便可以得到一定数量的PF分量:

最终信号x(t)可表示为k个PF分量和余量uk之和:
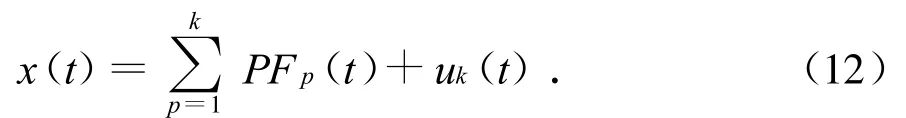
式中:uk(t)为残余函数,代表了信号的平均趋势.图1为转子系统质量不平衡时的振动加速度图.图2和图3分别为LMD,EMD分解图,LMD分解时其变量Δ=10-4.对比两图可知,信号分解后LMD方法的残差uk(t)比EMD方法的小.同时,LMD方法的端点效应也不如EMD方法明显.这是由于LMD方法是通过除以包络估计函数获得纯调频信号,从而使得迭代次数较少,因而端点效应不明显.而在EMD方法中,需要不断地“筛分”才能获得IMF,从而使得迭代次数多,因而端点效应明显.

图1转子系统质量不平衡故障振动信号Fig.1 Vibration signal of the rotor systems with mass unbalance

图2 转子系统质量不平衡故障振动信号的LMD分解结果Fig.2 The local mean decomposition results of the rotor systems with mass unbalance

图3 转子系统质量不平衡故障振动信号的EMD分解结果Fig.3 The empirical mode decomposition results of the rotor systems with mass unbalance
2 基于LMD和AR模型的转子系统故障诊断方法
基于LMD和AR模型的转子系统故障诊断方法步骤如下:
1)按一定的采样频率fs分别对转子系统的4种工作状态(正常、不对中、不平衡和油膜涡动)进行N次采样,得到4N个样本;
2)对每一个样本信号进行LMD分解,得到若干PF分量;
3)对任一PF分量PFp(t)建立如下的自回归模型AR(m)[9]:

采用FPE准则[9]确定模型的阶数m,ep(t)为模型的残差,其服从零均值分布,是均值为0、方差为的白噪声序列.由最小二乘法估计自回归参数φpk(k=1,2,…,m)和模型的残差方差,φpk表示第p个PF分量的第k个自回归参数;
3 转子系统故障诊断
为验证本方法的可行性,从转子故障试验台上分别测得转子正常、不对中、不平衡和油膜涡动4种状态下的振动信号各20组,采样频率为2 048 Hz,转速为6 000 r/min,从4类数据中随即抽取10组数据作为训练样本,将剩下的数据做为测试样本.
获得振动信号后,首先对转子故障振动信号进行LMD分解,然后建立AR模型,提取故障信息作为故障特征向量.从图2的分解结果中可以看出信号的主要信息主要包含在前两个PF分量中,因此选取前两个PF分量建立AR模型并提取故障特征信息.由于系统的状态主要由前几阶的自回归参数和模型残差的方差决定,因此本文选择了前5阶的自回归参数φpk(k=1,2,…,5)和模型残差的方差作为神经网络的输入参数.经过比较,神经网络的网络结构设定为12×18×4.由于本次试验一共有4种状态的转子振动信号,即正常、不对中、不平衡和油膜涡动,所以输出矩阵的状态编码为:正常(1,0,0,0);不对中(0,1,0,0);不平衡(0,0,1,0);油膜涡动(0,0,0,1).每种模式分别用10个样本进行训练,训练截止误差为0.00 001,学习速率为0.25,网络训练至收敛.用训练好的神经网络对测试样本进行分类,结果网络全部成功识别.表1给出了部分测试样本的识别结果.
为了比较EMD方法和LMD方法的分类效果,对转子振动信号均进行EMD分解,同样选取前两个IMF分量建立AR模型,提取前5阶自回归参数φik(k=1,2,…,5)和模型的残差方差作为特征向量输入神经网络.结果网络全部成功识别.表1给出了相同测试样本的识别结果.实验结果表明LMD方法和EMD方法均可以有效地对转子系统故障振动信号进行预处理,对各自的分量建立AR模型提取特征参数后,可成功地识别转子系统的工作状态和故障类型.

表1 测试样本的识别结果Tab.1 The recognize results of the test samples
4 结 论
LMD方法是一种自适应的信号分解方法,而AR模型是一个信息的凝聚器,可将转子系统的特性及工作状态都凝聚于其中,因而可依据它对转子系统的工作状态进行分析.但是,AR模型只能分析平稳信号,对具有非平稳特征的转子状态故障振动信号的分析效果不甚理想.因此本文针对转子系统故障振动信号的非平稳特征,采用LMD方法和AR模型相结合的方法对转子系统进行故障诊断,并与EMD方法进行了比较.研究结果表明,LMD方法和EMD方法一样都是将一个复杂信号自适应地分解为若干个瞬时频率具有物理意义的分量之和,每一个分量都与一定的物理过程相对应,因此两种方法均可以有效地对故障振动信号进行预处理,再对其各自的分量建立AR模型提取特征参数均可成功地识别转子系统的工作状态和故障类型.但是在对数据的分解效果方面,LMD方法要优于EMD方法,主要表现在两个方面:一是LMD方法分解后数据残差要比EMD方法的小;二是LMD方法在抑制端点效应方面要优于EMD方法.不过LMD方法也有其不足之处,如运算时间长、平滑时无法确定最优步长等,这些问题都有待在后续的研究中得到解决.相信随着这些问题的深入研究,LMD方法将会得到更广泛的应用.
[1] GUO D,PENG Z K.Vibration analysis of a cracked rotor using Hilbert-Huang transform[J].Mechanical Sy stems and Signal Processing,2007,21(8):3030-3041.
[2] 丁玉兰,石来德.机械设备故障诊断技术[M].上海:上海科学技术文献出版社,1994:225-230.DING Yu-lan,SHI Lai-de.Fault diagnosis of machanical equipment[M].Shanghai:Shanghai Scientific and Technological Literature Press,1994:225-230.(In Chinese)
[3] CHENG Jun-sheng,YU De-jie,YANG Yu.A fault diagnosis approach for roller bearings based on EMD method and AR model[J].Mechanical Sy stems and Signal Processing,2006,20(2):350-362.
[4] HUANG N E,SHEN Z,LONG S R.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analy sis[J].Proceeding s of the Royal Society of London Series,1998,454:903-995.
[5] DA TIG M,SCHLURM ANN T.Performance and limitations of the Hilbert-Huang transformation(HHT)with an application to irregular water waves[J].Ocean Engineering,2004,31(14):1783-1834.
[6] 程军圣,于德介,杨宇.基于支持矢量回归机的Hilbert-Huang变换端点效应问题的处理方法[J].机械工程学报,2006,42(4):23-31.CHENG Jun-sheng,YU De-jie,YANG Yu.Process method for end effects of Hilbert-Huang transfo rm based on support vector regression machines[J].Chinese Journal of Mechanical Engineering,2006,42(4):23-31.(In Chinese)
[7] SMITH J S.The local mean decomposition and its application to EEG perception data[J].Journal of the Royal Society Interface,2005,2(5):443-454.
[8] 程军圣,张亢,杨宇,等.局部均值分解与经验模式分解的对比研究[J].振动与冲击,2009,28(5):13-16.CHENG Jun-sheng,ZHANG Kang,YANG Yu,et al.Comparison between the methods of local mean decomposition and empirical mode decomposition[J].Journal of Vibration and Shock,2009,28(5):13-16.(In Chinese)
[9] 杨叔子,吴雅.时间序列分析的工程应用[M].武汉:华中理工大学出版社,1992:31-356.YANG Shu-zi,WU Ya.Engineer application of time series analysis[M].Wuhan:Huazhong University of Science and Technology Press,1992:31-356.(In Chinese)
