垂直轴风机的参数优化设计

2010-03-17刘桂霞

河北建筑工程学院学报 2010年3期

关键词：垂直轴风轮攻角

刘桂霞姚力

河北建筑工程学院

1 风力机的分类

风力机是风力发电的主要设备,其结构形式按照风轮旋转轴在空间的方向,可以分为水平轴风机和垂直轴风机两大类.

水平轴风机的风轮围绕一个水平轴旋转,工作时风轮的旋转平面与风向垂直.风轮上的叶片径向安置,与转轴垂直.水平轴风机具有扫风面积大,风能利用率高的优点,是目前商业化风力发电机组的主要形式.

垂直轴风机的风轮围绕一个铅直轴旋转,其主要优点是无需对风,结构简单,便于维修,气动噪音小;缺点是风能利用率低,不易自行启动.如果能够提高垂直轴风机的启动性能和风能利用系数,将会进一步降低风电的成本,对风力发电的发展起到巨大的促进作用[1].

垂直轴风机又分为两类:一类是利用空气阻力做功的阻力型风机,如S型风机;另一类是利用翼型的升力做功的升力型风机,典型结构是达里厄风机.升力型风机的风能利用率明显高于阻力型风机,且不会产生侧向推力,是现代水平轴风机的主要竞争者.

2 垂直轴风机的攻角变化分析

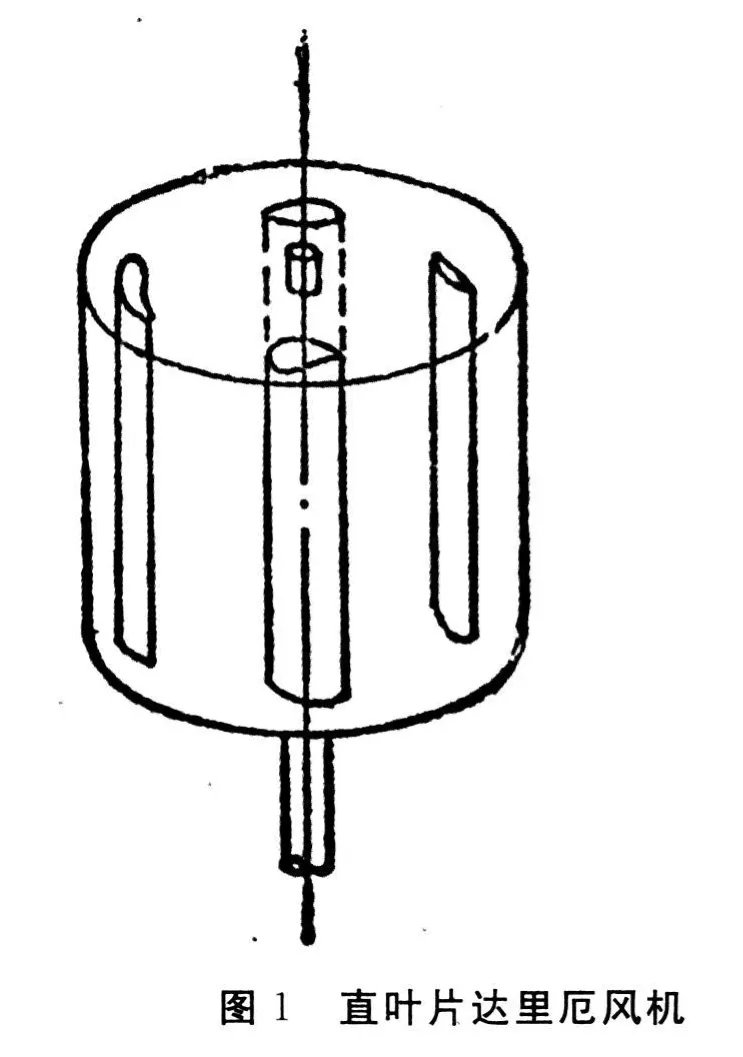
在此我们讨论直叶片达里厄风机,叶片弦长C恒定不变,叶片高度为2H.(图1)

分析图2所示弦长为C的叶素,其旋转半径为R,处于任意方位角θ处,叶片的安装角为β.设流过叶片的风速为v,叶片的切向速度u,(u=R ω),ω为叶轮的角速度.则风相对于叶片的速度为w,w=vu.攻角为α,是相对风速与叶弦方向的夹角.将相对速度沿切向和径向分解,可得:

可得相对速度的大小:

叶片在任意位置的攻角α与方位角θ的关系:

由(3)式可知,叶片旋转一周时,α+β随方位角的变化情况可用正弦函数近似表示,并且随着λ的增大,α+β的变化范围逐渐减小.当λ=2时,α+β在-30°～+30°之间,变化范围较大.

根据J.Templin的研究结果[2],尖速比λ与R/BC的关系为:

其中B为风轮叶片数目.

对于叶片处于不同位置时速度三角形的研究表明,除非叶素翼型的对称面与风速平行或接近,几乎在所有位置上作用力都产生驱动力矩.

相对风速与翼型之间的攻角不会超过极限值,即

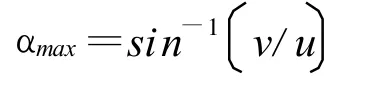
若风轮的圆周速度大于风速,叶片就可以满足小攻角的条件,保证叶片能够产生较大的力矩使风轮旋转.但如果风轮静止,攻角会很大,在某些位置将发生失速,此时达里厄风机需外力启动.

3 垂直轴风机的气动力分析及参数优化设计模型

流体流经翼型叶片时,不仅在来流方向产生阻力,而且在垂直方向产生升力.图2所示叶素位于任意位置θ,安装角为β.则作用于叶片的升力和阻力分别为:

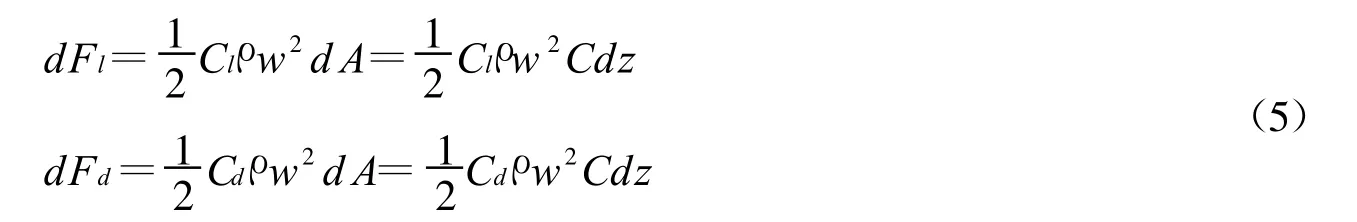
式中,ρ是空气密度,A是流面面积,C是叶片弦长,w是相对风速,Cl和Cd分别是升力系数和阻力系数,均与攻角α有关[3].

气动力在径向和切向的分量分别为:

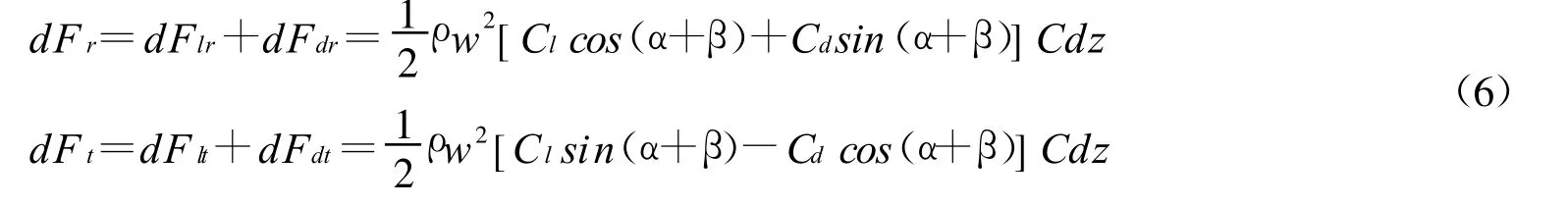
径向力作用在叶片和风轮轴上,切向力使转子产生转动力矩:

对于每一个叶片来说,叶素上的力随叶片的旋转而变化,需计算其平均值:

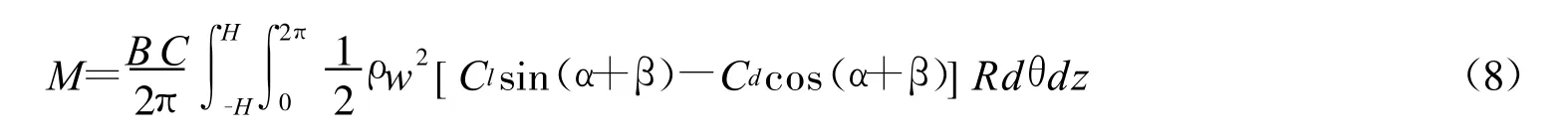
影响平均驱动力矩的非线性参数有叶片数目B,叶片弦长C,旋转半径R,升力系数Cl和阻力系数Cd及安装角β.

在满足小攻角条件下,为使风机获得较大的平均驱动力矩,需要对相关参数进行优化设计.其优化数学模型为:

求:B、C、R、Cl、Cd、β

4 算例

NACA0012型对称翼型的安装角优化设计

对给定的翼型NACA0012型对称翼型,升力系数、阻力系数与攻角之间的关系曲线确定(图3),通过分段拟合,得翼型的升力系数曲线多项式(10)和阻力系数曲线多项式(11)[4]:

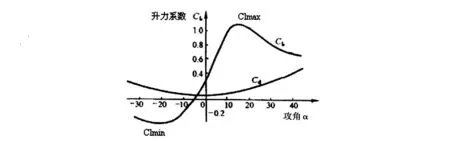
图3 翼型的升力、阻力系数曲线

以下关于安装角的优化进行讨论.选定风力机的基本参数如表1:

表1 风力机基本参数

叶尖速比λ=3.56时,-20°＜α+β＜20°

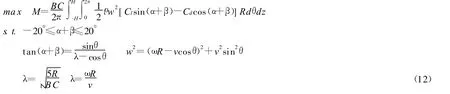
求:β优化方法:

模型(12)中,目标函数M是设计变量β的单峰函数,在满足约束条件下,可选取初值应用黄金分割法进行直线搜索.当β选取初值后,以1°角为区间,应用梯形复化公式求解函数的积分,以确定目标函数M.对于3叶片,最优安装角为-1.10°,最大平均扭矩值为7.644 kNm,对于4叶片,最优安装角为-0.95°,最大平均扭矩值为12.201 kNm.

为得到平均驱动力矩随安装角变化关系曲线,在-20°～+20°的范围内以1°安装角为间隔,对不同安装角下平均驱动力矩进行数值模拟,图4和图5分别为三叶片和四叶片风轮的平均驱动力矩随安装角的变化曲线图.应用最小二乘法对曲线进行二次拟合,得到图4对应的曲线方程为T=-0.1216β2-0.1438β+6.9638;图5对应的曲线方程为T=-0.1367β2-0.1501β+11.6331.

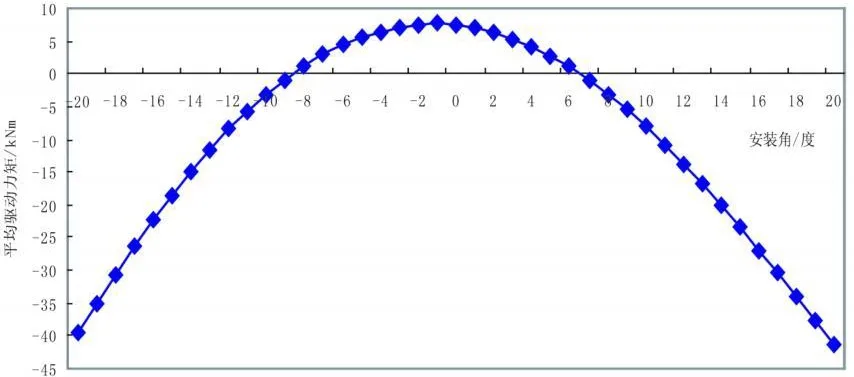
图4 三叶片风轮的驱动力矩随安装角的变化曲线

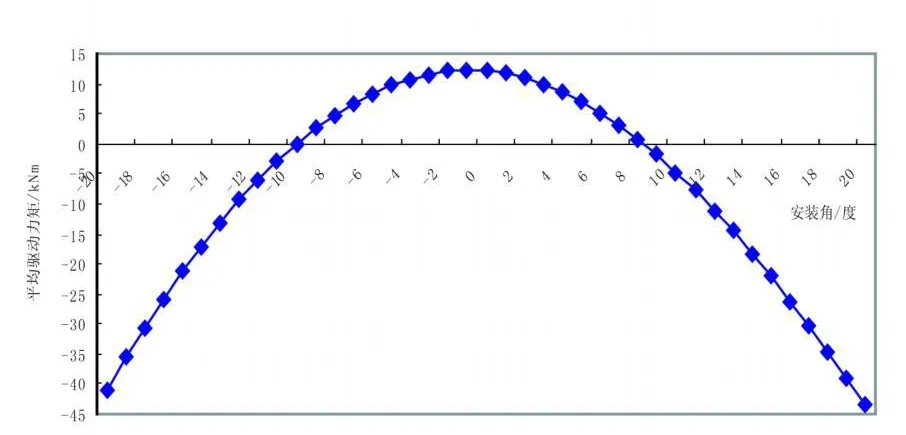
图5 四叶片风轮的驱动力矩随安装角的变化曲线

从图中可以看出,不论三叶片风轮还是四叶片风轮,都是在安装角接近-1°时获得最大驱动力矩;对三叶片风轮,当β＞+7°或β＜-9°时;而四叶片风轮,当β＞+9°或β＜-10°时将获得负的驱动力矩.从经济合理的角度,四叶片风轮比三叶片风轮多用33.3%的材料,而获得的最大驱动力矩与三叶片风轮相比增加了59.6%,因此,四叶片的风轮是比较好的选择.