基于塑性指数土的渗透系数经验关系的研究
2010-03-17王晓峰
王晓峰
(大连理工大学土木建筑设计研究院有限公司,辽宁大连 116023)
1 前 言
齐齐哈尔位于松嫩平原西部,区内堆积了巨厚的第四系松散堆积物,表层(0~10m)粉土、黏性土普遍分布。规律表明,塑性指数(IP)与渗透系数(k)呈明显的相关型。建立其区域经验关系,对确定该区域粉土、黏性土的渗透系数具有重要意义。
2 试验指标
所采用的IP与k对比数据,具有如下特征:
1)塑性指数IP的确定,液限为锥式法10 m m液限,塑限采用搓条法。
2)对比数据涵盖了齐齐哈尔市所辖县区内全部嫩干堤防,包括甘南堤防、梅里斯堤防、讷富堤防、齐富堤防400 k m堤段“工程地质勘察资料”中的全部试验数据。
3 相关分析
通过对Ip与l n(k)对比数据在直角坐标中做散点图分析(见图1),Ip与l n(k)对比数据线性相关,渗透系数k随着塑性指数的增大而逐渐减小。
3.1 回归方程的建立
由图 1可见,渗透系数k随着塑性指数 Ip的增大而减小,因此可以用y=a+b x表示两者之间的关系,用最小二乘法得:

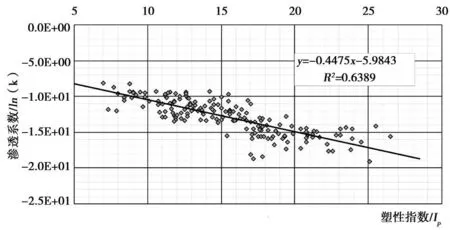
图1 土的塑性指数Ip与渗透系数l n(k)经验关系散点图
3.2 回归方程的计算
回归方程的计算就是求回归系数 b和常数项 a,可分别按上述两式计算。各计算项结果详见表 1。
将表 2中有关数据代入上述两个计算式中求得:

所以Ip与l n(k)回归方程为:l n(k)=-0.4475Ip-5.9843,

3.3 相关系数
相关系数公式为:


表1 一元线性回归方程计算结果表
将表1中数据代入(3)式求得相关系数r=-0.80
3.4 回归方程显著性检验
利用方差分析法进行检验,其检验过程为:
1)计算总平方和Lyy及其自由度fyy

2)计算回归平方和U及其自由度fU

3)计算剩余平方和Q及其自由度fQ
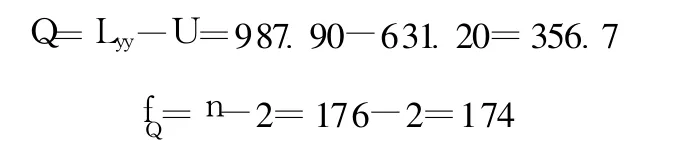
显著性评价结果,详见表 2。

表2 方差分析表
由表3可见,Ip与l n(k)经验关系高度显著。
4 结 语
1)经验关系适用范围为:Ip数值区间为 7~26.5,适用的土类为低液限粉土 ~高液限黏土。
2)经验关系表根据经验关系k=2.52×10-3e-0.4475Ip,建立塑性指数(IP)与渗透系数(k)经验关系表,见表3。

表3 土的塑性指数Ip与渗透系数k经验关系表
3)由经验关系及表4可以得出土的渗透系数(k)随着塑性指数(Ip)的增大而逐渐减小,土的类别与渗透系数的关系为:
粉土:k≤2.87×10-5;
粉质黏土:k=1.25×10-6~2.87×10-5;
黏土:k=1.43×10-8~1.25×10-6。
由于所建立的塑性指数(Ip)与渗透系数的经验关系高度相关,在本区域查表确定土的渗透系数,可大大地提高土的渗透系数的确定精度及工作效率。该经验关系对松嫩平原西部地区土的渗透系数的确定具有积极的指导作用及重要的理论意义。
[1] 中华人民共和国水利部.G B/T 123-1999土工试验方法标准[S].北京:中国计划出版社,1999.
[2] 常士骠.工程地质手册(第三版)[R].北京:中国建筑出版社,1992.
[3] 胡广韬,等.工程地质学[M].北京:地质出版社,1984.
