基于循环统计量分析方法诊断轴承故障的研究

张燕

（哈尔滨轴承集团公司质量管理部，黑龙江哈尔滨150036）

1 前言

由于旋转机械的工作方式是周期性的转动，在其振动信号中既包含大量的随机成分，同时也包含周期成分，因而旋转机械的振动信号是一种特殊的非平稳信号，呈现周期性的平稳特性，即循环平稳信号[1]。许多旋转设备的机械故障表现为循环平稳特性，例如轴承[2]、齿轮等，其故障信号被淹没在大量的随机信号中，同时呈现出周期性。应用一般的平稳信号处理方法难以发现这些故障频率，基于循环统计理论的循环谱密度分析方法能够将这些信号中的故障冲击频率分解出来。

2 循环统计原理

2.1 循环遍历性

设有一个零均值的非平稳信号χ（t），其时变自相关函数定义为:

如果已知该信号的时变自相关函数具有周期为0的特性，并对循环平稳信号以0为周期进行采样，由于该采样序列等于原随机过程，这样的采样值显然满足遍历性[3]，从而可以用时间平均来代替统计平均。假设循环平稳过程所含的周期为T0，则循环平稳信号的自相关函数为：

式中：N为数据个数。

循环平稳过程具有的遍历性称为循环遍历性。循环平稳过程的时间平均与平稳遍历过程的时间平均是有区别的，主要表现在两个方面[4]：

（1）平稳遍历过程的时间平均是对信号在总观测时间上的平均，而循环平稳过程的时间平均是对信号以循环周期采样后的总采样点数进行平均；

（2）平稳遍历过程的时间平均是对所有的连续信号的时间平均，而循环平稳过程的时间平均只对循环周期上的离散采样信号。

2.2 二阶循环谱密度

循环平稳过程的统计特征和物理意义可以用二阶循环谱密度来描述，即对循环平稳信号的二阶统计量进行傅里叶变换，从频率域来描述信号。式(2)定义了循环平稳过程的自相关函数。由于循环平稳信号的统计量是周期函数，因此对该式用傅里叶级数展开，得到：

式中：m=1,2,3…；

a=m/T0，

其傅里叶系数为：

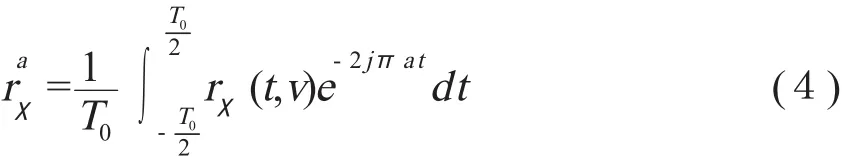
将式(2)代入式(4)中，整理得：

由式(5)可知，若取a＝0，则有：

对循环平稳信号而言，可以通过傅里叶变换从频率域中描述信号的二阶循环统计量。循环自相关函数对数的傅里叶变换为循环谱密度函数，也称谱相关函数，用S(f)表示，即：

谱密度函数也是二阶循环统计量，它的图形表示称为循环谱。由上述分析可知，循环统计量是时变统计量在循环频率域上的分解或展开。由于许多旋转机械振动信号的循环平稳性表现在二阶统计量上，并且二阶循环统计量用三维空间表示分析结果，对实际对象的物理意义解释明确[5]。

3 仿真信号

当旋转设备出现故障时，会产生一定的冲击，这些冲击激发相应零部件的固有频率，产生频率成分复杂的振动信号，例如当轴承发生故障时，其故障表面会与其他表面产生撞击，从而产生与故障特征频率相联系的特征信号[6]。在大量随机噪声和众多零部件固有频率的覆盖下，这些故障冲击频率难以通过平稳信号分析方法获得。然而由于这些冲击信号具有二阶周期性的循环平稳特性，应用循环谱密度分析方法可以有效地提取冲击频率。

设有一振动冲击信号，冲击频率f1＝83Hz，被冲击零部件的固有频率f2＝250 Hz，采样频率fs＝10kHz，并伴有大量的随机噪声信号，得到如图1所示的冲击仿真信号的时域波形和频谱。

在该信号的频谱图中，出现了零部件的固有频率f2＝250Hz，但故障冲击频率被大量的随机信号所湮没，难以识别。利用循环谱密度分析方法对该仿真信号进行分析，得到如图2所示的循环谱密度三维图。在该冲击信号的循环谱密度三维图中，循环频率a＝83Hz处出现了明显的峰值，与模拟信号的冲击频率一致。可见，应用循环谱密度三维图能够清楚地将冲击源的频率在循环频率轴上凸显出来，从而有利于提取旋转设备的一些冲击信号特征。

4 滚动轴承振动信号

一台反冲洗水泵在日常定期振动监测时，发现该泵靠近电机端振动较大，并超过标准JB/T 8097-1999中规定的限值。该泵为立式深井泵，额定转速1 480 r/m in。在靠近电机端安装有一个角接触球轴承，轴承型号为SKF7317，所测振动信号的时域波形如图3（b）所示。

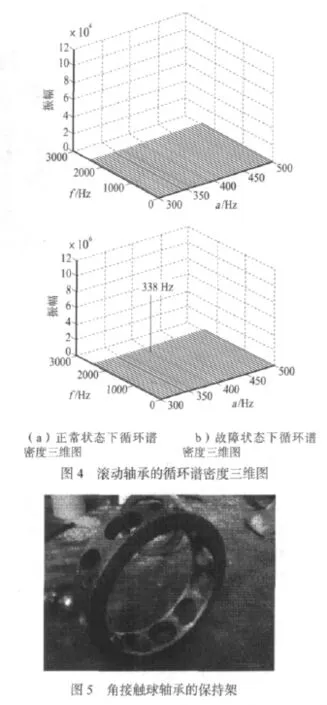
对比正常的振动时域波形可以发现，在故障状态下，时域波形存在频率较高的冲击振动现象，并且是导致振动幅值增大的主要原因。应用循环谱密度分析方法作正常状态和故障状态的循环谱密度三维图，如图4所示。

在正常状态下，信号的整体振动幅值水平较低，不存在明显的振动峰值。而在故障状态下，整体振动幅值水平较高，且在循环频率a＝338H z处出现了明显的振动峰值。该频率即为对应的故障冲击频率。对该设备解体检修发现，角接触球轴承的保持架内侧存在两条明显摩擦痕迹，如图5所示。结合设备振动状态，在设备运转期间，内环和保持架之间存在刚性碰摩，并由于摩擦发热，使两者之间的摩擦加剧，产生大量的振动和冲击信号。通过循环谱密度分析信号循环频率域，能够发现旋转设备中存在的冲击故障频率。

5 结束语

在现代工厂和企业中，旋转机械占据了工厂中设备的绝大多数。旋转机械运行状态的好坏往往反映出工厂的整体运行情况。然而大多数旋转设备由于其工作条件和环境的复杂性以及机组运行状态的变化等，其故障信号难以被检测。

本文利用旋转设备的振动信号为循环平稳信号，根据循环统计量周期变化的信息，应用循环统计理论，分离出旋转设备的零部件固有频率和故障冲击频率。通过对仿真信号和实测信号的分析表明，循环谱密度分析方法具有较好的诊断效果。

[1]张贤达.非平稳信号分析与处理[M].北京：国防工业出版社，1998.324-336.

[2]李力，屈梁生.循环统计方法在滚动轴承故障诊断中的应用[J].振动、测试与诊断，2003，23(2)：116-119.

[3]张贤达.时间序列分析—高阶统计量方法 [M].北京：清华大学出版社，1996.

[4]李力.机械信号的循环统计处理原理和应用[D].西安：西安交通大学，2004.12-17.

[5]史庆峰.基于灰色理论和循环统计量的发动机故障诊断方法研究[D].西安：西安交通大学，2007.40-41.

[6]陈仲生，杨拥民，胡政等.基于循环统计量的直升机齿轮箱轴承故障早期检测[J].航空学报,2005，26(3)：371-377.（编辑：林小江）